지난 포스팅에서는 배열을 이용한 큐를 구현해보았다.
front, back 변수를 모두 0으로 초기화 하였을 때,
push: back 변수가 가리키는 인덱스에 데이터 추가, back >= size 이면 오버플로우
pop: front 변수가 가리키는 인덱스의 데이터를 제거, front >= back 이면 언더플로우
와 같이 구현할 수 있었다.
그러나 이렇게 구현하면 push 를 최대 N번, pop은 push 횟수 이하로만 할 수 있다는 문제가 있었다.
이번에는 Size N 이라는 메모리 공간에 중간중간 여유가 생긴다면
그 여유공간까지 활용하여 push 를 더 많이 할 수 있도록 기존의 큐를 개선하여 보겠다.

그림과 같이 사이즈 5인 큐에 모든 값이 다 들어있는 상황을 생각해보자.
현재 front 는 2이고, back 은 8이다. ( 이전 포스팅에서 작성한 front, back 변수의 의미와 별개이다.)
이 상황에서 Pop을 해보자.

front에 있는 2가 나오고, 0번 인덱스의 값이 비게 된다.
이전 포스팅에서 구현한 큐에서는 이 상황에서도 큐에 데이터를 push 할 수 없었다.
하지만 저렇게 빈 메모리 공간이 있고, 어차피 다음 데이터가 pop 될 위치도 인덱스 1로 결정된 상황에서 빈 메모리 공간을 활용하지 못하는 것은 매우 아쉽다.
이를 해결하기 위해 Circualr Queue 를 구현해볼 것이다.
Circular Queue는 이름에서 나와있듯, Queue 의 첫번째 인덱스와 마지막 인덱스가 연속되어 있다고 생각하는 자료구조이다.
그림으로 표현하면 이런 형태가 된다.
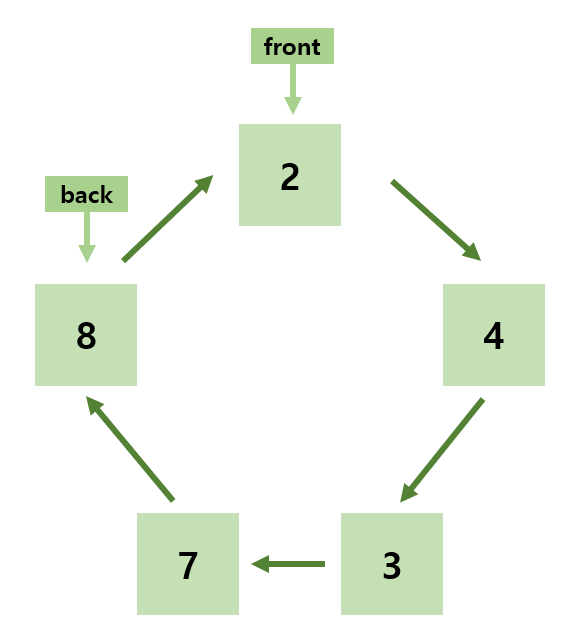
데이터를 pop 할 때는 front 위치의 데이터가 빠져나오고,
데이터를 추가할 때는 back 위치 다음 위치에 데이터가 추가된다.
아래 이미지는 데이터를 pop 하는 경우를 보여준다.

이렇게 circular 형태로 된 큐라면 이 상황에서 back 다음위치에 데이터를 새로 push 하는 것이 어색하지 않다.
그러나 우리는 이 자료구조를 '선형' 자료구조인 배열에서 구현해야 한다.
구현하는 방법은 front, back 변수를 두고 구현하는 기존 구현과 큰 차이가 없다.
우선 기존 구현과 똑같이
front: 현재 데이터가 존재하는 인덱스, front 위치의 데이터를 pop 한다.
back: 앞으로 추가될 데이터가 위치할 인덱스, back 위치에 데이터를 push 한다.
이렇게 정의하고 구현해보자.
그러면 기존 구현과 마찬가지로 front = 0, back = 0 으로 초기화 된다.
Q[N]: Array of size N
init: front, back
front <- 0
back <- 0
우선 선형 자료구조에 하듯 큐의 push 를 구현해보자.
push(x) {
if (back >= N)
OVERFLOW!
Q[back] <- x
back++
}이 구현에서는 큐에 데이터를 추가할 수 있는지 판단할 때 N 을 이용했다.
한번 이렇게 생각해보자.
큐에 데이터를 추가할 수 없다는 의미는 무엇일까?
데이터가 '큐의 사이즈' 만큼 꽉 찼다는 의미이다.
그렇다면 '큐의 사이즈' 는 무엇일까?
우리가 정의한 front, back 변수 의미대로라면 큐의 사이즈는 다음과 같이 정의된다.
size <- abs(back - front)abs 는 절댓값을 취하는 함수이다.
상황에 따라서 front 가 back 을 넘는 상황이 충분히 발생할 수 있다.
따라서 데이터를 넣을 수 있는지 없는지 판단할 때는 이 size 값을 이용해서 판단하면 된다.
데이터의 추가 위치는 어떻게 알 수 있을까?
이는 기존과 동일하다.
back 이 가리키는 위치에 넣고, back 을 +1 하면 된다.
그런데 back 변수는 0 <= back < N 범위에 존재해야 한다.
그렇기에 N을 넘어가게 되면 N으로 나눈 나머지를 저장해주어야 한다.
이를 정리하여 구현하면 아래와 같이 구현된다.
push(x) {
size <- abs(back - front)
if ( size >= N)
OVERFLOW!
Q[back] <- x
back++
back <- back % N
}pop 도 마찬가지로 size 를 이용하면 된다.
먼저 기존에 구현했던 pop 코드를 보자.
pop() {
if (back - front <= 0)
UNDERFLOW!
x <- Q[front]
front++
return x
}아까 size = abs(back - front) 라고 하였다.
위 코드에서도 size 에 대한 부분이 담겨 있으므로, abs 만 해주면 되겠다.
또 front 값이 1 증가하였을 때, N 이상이 될 수도 있으므로, front 값도 나머지 연산을 해주어야한다.
최종적인 pop 코드는 아래와 같이 된다.
pop() {
size <- abs(back - front)
if (size <= 0)
UNDERFLOW!
x <- Q[front]
front++
front <- front % N
return x
}종합한 전체 원형 큐 코드를 보면 아래와 같다.
Q[N]: Array of size N
init: front, back
front <- 0
back <- 0
push(x) {
size <- abs(back - front)
if ( size >= N)
OVERFLOW!
Q[back] <- x
back++
back <- back % N
}
pop() {
size <- abs(back - front)
if (size <= 0)
UNDERFLOW!
x <- Q[front]
front++
front <- front % N
return x
}'CS > 자료구조' 카테고리의 다른 글
| [자료구조 및 프로그래밍] 5. Stack & Queue With Linked List (0) | 2023.10.17 |
|---|---|
| [자료구조 및 프로그래밍] 4. Linked List (0) | 2023.10.12 |
| [자료구조 및 프로그래밍] 2. Queue (implement with Array) - 1 (2) | 2023.09.30 |
| [자료구조 및 프로그래밍] 1. Stack (implement with Array) (2) | 2023.09.21 |
| [자료구조 및 프로그래밍] 0. 주소록 프로그램과 array (배열) (0) | 2023.09.17 |
