그림과 같이 100만개의 랜덤 성생된 정수가 있다.
이 정수를 각 정렬 방법으로 정렬해보려고 한다.
(100만개를 N^2 시간에 정렬하면 시간이 오래 걸려서, 실제로는 100, 200, ..., 900 단위로만 정렬해 볼 것이다.)
정렬을 수행하면서, 비교는 몇번 일어나는지, 정렬을 하기 위해, 기존 배열에 (또는 새로 생성한 배열에) 데이터를 쓰는 행위를 몇번이나 하는지 횟수를 세보고자 한다.

이를 위해 먼저 100만개의 정수가 담긴 데이터를 ' ' 기준으로 끊어 배열에 저장한다.
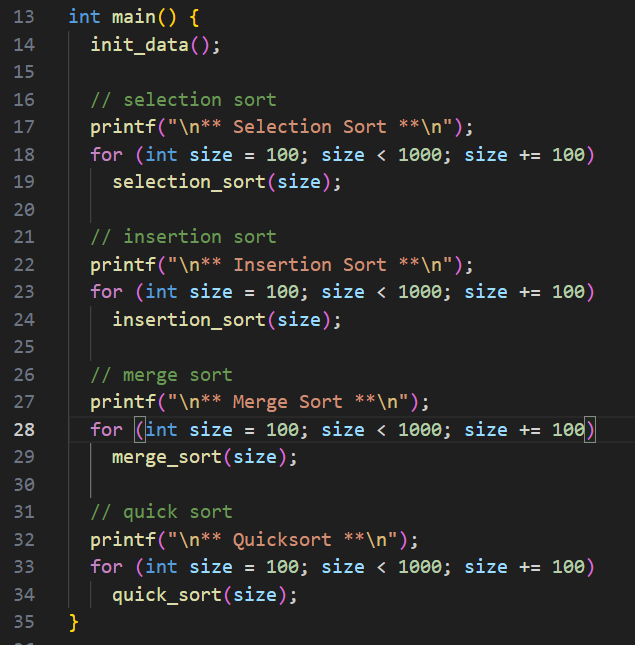
그리고 각 정렬을 수행한다.
정렬은 사이즈가 100, 200, 300, ..., 900 인 상황을 매번 수행해보면서, 그 때의 비교횟수와 데이터 쓰기 횟수를 카운팅한다.
차례대로 정렬을 구현하고, 횟수를 카운팅한 결과를 출력해보자.

이때 그림과 같이 C1 = 키값 비교 횟수, C2 = 정렬을 위해 배열에 데이터를 쓰는 연산을 수행한 횟수를 세었다.
선택 정렬
선택 정렬은 제일 왼쪽 원소부터 하나씩 고르고, 그 원소를 자신보다 뒤에 있는 원소 중 제일 작은 최솟값과 교환하는 방법으로 정렬을 수행한다.
총 N개의 데이터가 있을 때, 자신 뒤에 원소가 없는 맨 마지막 원소를 제외하고 나머지 원소들에 대해서 이를 반복하면 된다.
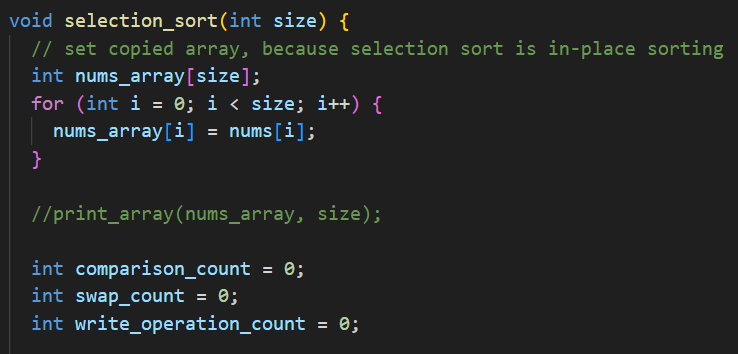
우선 selection_sort 는 in-place 정렬 방식이다.
따라서 기존 데이터를 읽어왔던 초기 배열의 순서를 바꾸지 않기 위해 배열을 따로 임시 공간에 복사해두었다.
이 과정에서 wirte를 수행한 횟수는 카운팅하지 않았다.

선택 정렬의 정렬이 일어나는 코드다.
i 가 실행되는 범위가 size 가 아니라 size-1 보다 작을 때까지 라는 점을 유의하자.
비교 횟수를 카운팅하는 부분은 (min_value > nums_array[i]) 라는 비교를 몇번이나 하는지를 카운팅하는 것이다.
제일 작은 값의 인덱스를 구한 이후 swap 을 수행하면 swap_count가 1 증가한다.
그리고 데이터를 쓴 횟수를 2만큼 증가시킨다. swap 함수로 인해 배열에 값을 2번 쓰기 때문이다.
총 비교 횟수는 N-1 + N-2 + N-3 + ... 1 = N(N-1)/2 만큼 발생하고,
총 데이터를 쓴 횟수는 swap횟수 * 2 이며, swap은 N-1 번 발생하므로 2(N-1) 이다.
프로그램 실행 결과는 아래와 같다.

그림에서는 swap을 언제나 반드시 수행하도록 구현하였는데, 만약 swap 할 필요가 없다면 swap을 생략해도 된다.
그래서 쓰기 횟수는 실제로는 좀 더 줄어들 수 있다.
그래서 강의록에서는 swap 횟수 <= N-1 이라고 표기해두었다.
(하지만 이 경우, swap을 할 필요가 있는지 없는지를 if 문으로 체크해야 하므로 비교를 한번 더 해야 하긴 한다.)

그 경우 이렇게 코드를 작성할 수 있다.
이때 비교는 인덱스를 비교하는 거라서 키값 비교로는 볼 수 없다고 생각해 비교 횟수에 카운팅하지는 않았다.
nums_array[i] != num_array[min_idx] 로 비교한다고 하면 할 말은 없지만.. 일단 굳이 그렇게 안하고 인덱스만으로도 판별이 가능하다.
이 경우 실행결과는 아래와 같이 나온다.

이렇게 데이터를 쓰는 횟수가 조금 감소하였다.
삽입 정렬은 언제나 비교 횟수가 언제나 N(N-1)/2 번으로 고정되어 있다.
그러나, 데이터를 읽고 쓰는 횟수는 데이터의 종류에 따라 바뀔 수 있다.


데이터가 이미 정렬된 채로 들어오는 최선의 경우, 데이터를 쓰는 횟수는 0번이다.
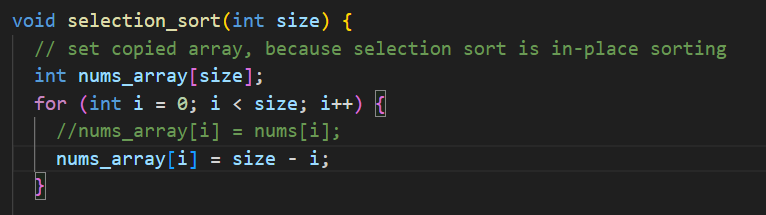

데이터가 모두 역순 정렬된 채로 들어오는 경우, 비교횟수는 고정되어 있고, 쓰는 횟수는 N 과 같다.
마치 최악의 경우처럼 보였지만 2(N-1) 이 되지 않는 이유가 뭘까?
그 이유는 1번째 데이터와 N 번째를 교체하는 순간 1번째 데이터와 N 번째 데이터를 모두 동시에 정렬한 것과 같은 효과가 생겨 N/2 번의 교환만 하면 되고, 이에 따라 쓰기는 N 번만 하면 되기 때문이다.
선택 정렬에서의 최악의 경우는 아래와 같이 데이터가 이미 정렬되어 있는데, 최솟값만 배열의 맨 뒤에 가있는 상황이다.

swap 을 할 때마다 그 다음 최솟값이 맨 뒤로 가는 구조이므로, swap을 정렬이 끝날 때까지 항상 해야만 한다.
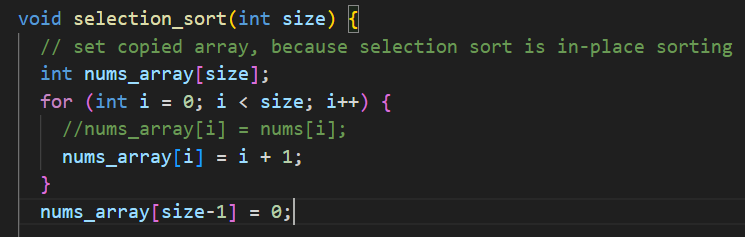
그 경우는, 데이터를 이렇게 세팅할 수 있다.

실행 결과로 최악의 쓰기 횟수인 2(N-1) 이 나온다.
< 선택 정렬 >
in-place : O
비교 횟수 : N(N-1)/2 = O(N²)
쓰기 횟수(최대) : 2(N-1) = O(N)
쓰기 횟수(최소) : 0
삽입 정렬
삽입 정렬의 경우에도, in-place 로 버퍼없이 정렬을 내부적으로 수행한다.

그래서 마찬가지로 기존 배열이 변경되지 않도록 배열을 복사하여 정렬을 수행한다.
삽입 정렬의 알고리즘을 간단하게 복습하면 아래와 같다.
현재 정렬하려는 원소의 왼쪽은 이미 정렬되어 있는 상태라고 가정하고, 현재 원소를 이미 정렬된 원소의 어디에 들어가야 하는지 위치를 찾아 그 곳에 자신을 끼워 넣는다.
배열에서는 중간에 insert 하는 작업을 수행하려면 그 뒤의 원소를 모두 한칸 뒤로 밀어야 하기 때문에 이를 구현하기 위해 자신의 바로 왼쪽 값이 자신보다 크다면 swap 하는 과정을 반복하는 것으로 구현한다.
이를 모든 원소에 대해 반복하면 된다.
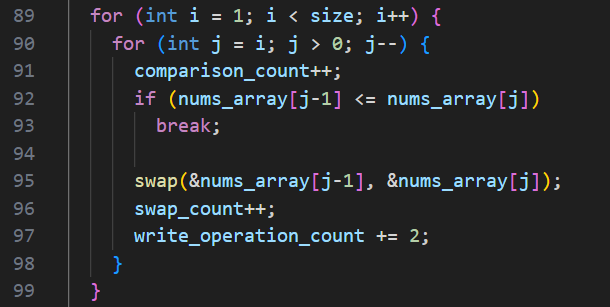
코드로 작성하면 위와 같다.
강의록에 적힌 예제 출력값과 달라서 여러번 검증해봤는데, 카운팅 방식에 문제는 없어보인다.
위에 설명한 알고리즘을 그대로 코드로 구현하였다.
출력값은 아래와 같다.
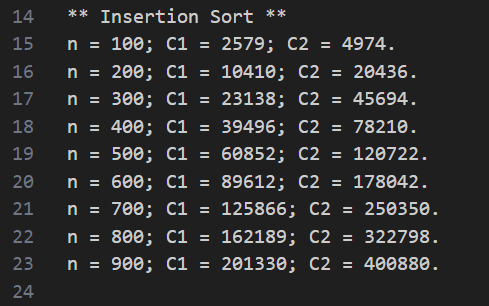
selection sort 와 비교하였을 때, 비교횟수는 거의 절반 가까이 줄어들었다.
그러나 선택 정렬은 비교 결과로 찾아낸 값을 한번만 swap하므로 swap횟수가 매우 적었지만,
삽입 정렬은 비교할 때마다 높은 확률로 swap을 수행하고, 한번 swap을 수행하면 배열에 데이터를 2번 쓰므로 거의 비교횟수의 2배에 가까운 쓰기 연산을 수행한다.

강의록의 비교 횟수와 쓰기 횟수는 이렇게 나왔는데, 데이터 Input 이 다른지 모르겠지만 어떻게 데이터를 쓰는 횟수가 비교 횟수와 비슷하게 나왔는지 모르겠다.
삽입 정렬은 최선의 경우 (이미 데이터가 정렬되어 있는 경우) N-1 번의 비교만 하고 교체는 없으므로 아주 빠르게 정렬을 수행할 수 있다.
최악의 경우 (데이터가 역순으로 정렬되어 있는 경우) N-1 + N-2 + ... + 1 = N(N-1)/2 번의 비교를 수행하고, 매 비교마다 모두 swap 을 수행하므로, 교체 횟수 역시 N-1 + N-2 + .... + 1 = N(N-1)/2 번의 교체를 수행한다.
한번 인풋값으로 최선의 데이터와 최악의 데이터를 넣어보자.

그림과 같이 이미 정렬된 상태의 데이터를 입력으로 설정하였다.

실행 결과, N-1 번의 비교를 수행하고 데이터를 읽고 쓰는 행위는 전혀 없다.
이렇게 정렬된 데이터를 넣는 경우가 최선의 경우이다.
삽입 정렬에서 최악의 경우는 선택 정렬과 다르게 데이터가 역순으로 주어질 때이다.
현재 보고 있는 원소의 왼쪽에 있는 데이터는 언제나 자신보다 항상 큰 원소이므로, swap 을 왼쪽에 있는 데이터의 개수만큼 진행하고, 또 그만큼 비교도 수행하기 때문이다.
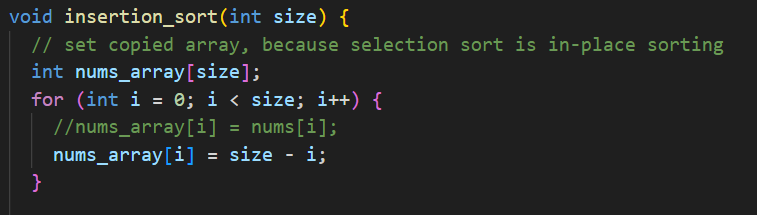
이렇게 역순 데이터를 입력으로 주면

이때는 비교횟수도 선택정렬과 동일하게 N(N-1)/2 번으로 나오는 한편, 쓰기 횟수는 N(N-1)/2 라는 swap 횟수에 2를 곱하므로 N(N-1) 번 쓰기를 수행한다.
결론적으로 삽입 정렬의 비교횟수와 쓰기 횟수는 아래와 같다.
< 삽입 정렬 >
in-place : O
비교 횟수(최대) : N(N-1)/2 = O(N²)
비교 횟수(최소) : N-1 = O(N)
쓰기 횟수(최대) : N(N-1) = O(N²)
쓰기 횟수(최소) : 0
선택 정렬 vs 삽입 정렬
| 선택 정렬 | 삽입 정렬 | |
| in-place 여부 | O | O |
| 비교 횟수 (최대) | N(N-1)/2 = O(N²) | N(N-1)/2 = O(N²) |
| 비교 횟수 (최소) | N(N-1)/2 = O(N²) | N-1 = O(N) |
| 쓰기 횟수 (최대) | 2(N-1) = O(N) | N(N-1) = O(N²) |
| 쓰기 횟수 (최소) | 0 | 0 |
선택 정렬은 비교 횟수가 N^2으로 고정되어 있지만, 쓰기 횟수가 최선과 최악의 경우 모두에 대해 크지 않다는 장점이 있었다.
삽입 정렬은 비교 횟수가 최선의 경우 N-1 이고, 최악의 경우에 가야 N^2 이 되므로, 선택정렬보다 적은 비교횟수를 가지는 장점이 있었다.
그러나 최선의 경우, 최악의 경우 모두 비교할 때마다 거의 swap을 수행하기에 비교 횟수 2배에 가까운 쓰기를 수행해야 했다.
이는 최악의 경우에는 정말 많은 쓰기 연산을 수행해야 하는 점이 단점이 된다.
따라서 삽입 정렬은 비교적 정렬이 잘 되어있는 데이터에 대해 추가적인 정렬을 수행하는 경우, 빠르게 정렬을 수행할 수 있다.
'CS > 자료구조' 카테고리의 다른 글
| [자료구조 및 프로그래밍] 17. 정렬의 최소 시간 복잡도 (0) | 2023.12.12 |
|---|---|
| [자료구조 및 프로그래밍] 16. O(N log N)정렬 방법 별 비교 횟수, 쓰기 횟수 비교 (0) | 2023.12.11 |
| [자료구조 및 프로그래밍] 14. 정렬 (선택정렬, 삽입정렬, 퀵소트, 머지소트, 기수정렬) (0) | 2023.12.09 |
| [자료구조 및 프로그래밍] 13. Binary Search & Sequential Search (0) | 2023.12.05 |
| [자료구조 및 프로그래밍] 12. Hashing & Hash Table (0) | 2023.12.02 |
