정렬의 종류별 알고리즘에 대해 정리할 때, 기수 정렬의 시간복잡도는 O(N)이 나왔었다.
그런데 일반적으로 정렬의 시간 복잡도는 O(N log N) 으로 알려져있다.
어떻게 기수 정렬은 O(N) 시간에 정렬을 할 수 있었을까?
그리고 왜 일반적으로 정렬의 시간 복잡도는 O(N log N) 으로 알려져 있는 걸까?
한번 O(n log n) 시간으로 고정되어있는 merge sort 의 comparison 과정을 tree로 표현해보자.

a, b, c, d 라는 4개의 데이터에 대해 merge sort 를 수행하면, 반씩 쪼개다가 merge 하는 과정에서 비교를 수행한다.
이때 비교를 통해 정렬을 수행하는 모든 경우의 수를 comparison tree 로 그려보자.
제일 먼저 비교가 일어나는 부분은 a, b 이다.
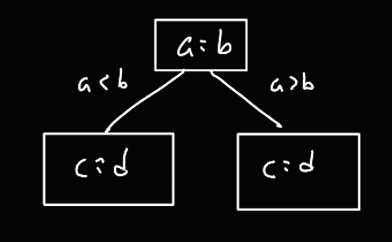
a, b 비교를 한 뒤, 그 결과를 확인하고, 다음으로는 c, d 를 비교한다.
c, d 의 비교 결과 정렬이 되면, < a, b, c, d > 4개를 정렬할 차례가 온다.

a, b 를 비교한 결과가 a < b 이고, c, d 를 비교한 결과 c < d 라고 하자.
그러면 지금 <a, b> <c, d> 이렇게 정렬된 두 배열이 존재한다.
이제 이 배열을 크기가 4인 정렬된 배열로 합친다고 하면, 제일 앞에 있는 원소를 비교하므로 a, c 를 비교 하게 된다.
만약 c, d 를 비교한 결과가 c > d 였다면 <a, b> <d, c> 이렇게 정렬된 두 배열이 존재할 것이고, 각 배열의 제일 앞에 있는 원소인 a, d 를 비교할 것이다.
그래서 위 그림과 같이 비교 트리가 그려진다.
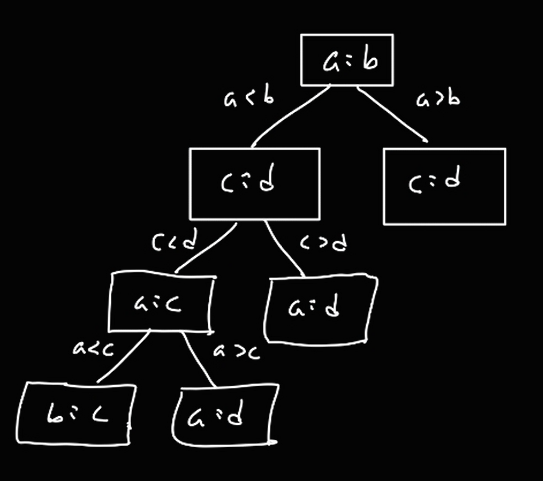
만약 a < c 라면, 그 다음으로 b 와 c 를 비교할 것이다.
merge sort 과정을 머릿속으로 그려보자.
만약 a > c 라면, c 가 정렬된 첫 원소로 들어가고, c 가 들어있던 배열의 c 다음 원소인 d 를 a와 비교할 것이다.
이런 식으로 비교 과정을 경우의 수를 따라 쭉 트리로 그려보면 아래와 같다.

이렇게 마지막에는 정렬 결과가 나온다.
공간상 여유가 없어 나머지 부분은 그리지 않았지만, 이런 comparison tree 는 정렬 방법과, 초기 input 데이터가 주어졌다면, 그 정렬 방법에 따라 tree 를 그릴 수 있다.
그림을 보면 이 comparison tree 의 leaf 노드는 언제나 '정렬된 결과' 를 나타내므로, N개 데이터를 정렬할 때 올바르게 작성한 comparison tree의 leaf node 개수는 N! 개 이다.
그리고 root 노드부터 leaf node까지의 경로는 정렬 결과가 나오기까지 어떤 과정으로 비교를 수행했는지를 나타내며, 이 경로의 길이가 해당 정렬 결과를 내기까지 비교횟수를 나타낸다.
따라서 이 비교 트리의 높이는 이 정렬 알고리즘의 최대 비교 횟수와 동일하다.
이 비교함수 트리는 '키 값 비교' 기반 정렬의 트리로써, 키 값을 비교한 결과는 항상 2가지 경우로 나타나기에 이 트리는 extended binary tree 로 볼 수 있다.
extended binary tree 에서 N 개의 leaf 노드를 가지는 트리의 높이는 최소 ⌈ lg N ⌉ 이다.
따라서 N! 개의 leaf node 를 가지는 트리의 높이는 최소 ⌈ lg N! ⌉ = Ω(n log n) 이므로, 정렬 시간은 O(n log n) 이상 시간이 소요될 수 밖에 없다.
참고로 log(N!) 이 n log n 이 되는 과정은 2가지 방법으로 확인할 수 있다.
첫번째로, e^N < N! < N^N 임이 잘 알려져 있기 때문에, stelling formular 를 이용하여 log(N!) = n log n 이 되는 것을 확인할 수 있다.
두번째는 적분을 이용하는 것이다.
log (N!)
= log N(N-1)(N-1)...(1)
= log N + log(N-1) + ... log(1)

이는 위 그림과 같이 log 그래프에 가로 길이가 1인 간격의 막대그래프를 세워놓고 적분을 하는 것과 같다.
log x 의 적분은 x log x 이므로 n log n 시간이 소요되는 것을 알 수 있다.
그럼 다시 처음의 의문으로 돌아와서, 정렬에는 최소 n log n 시간이 소요되는 것을 증명하였는데,
왜 기수 정렬은 O(n) 시간에 정렬을 할 수 있었던 걸까?
이는 기수 정렬이 '비교 기반' 정렬이 아니기 때문이다.
기수 정렬은 데이터의 종류의 유사성(3자리 숫자가 들어온다)을 가정해 그 유사성을 토대로 범위가 고정되어 있어 선형 시간에 정렬이 가능하다.
'CS > 자료구조' 카테고리의 다른 글
| [자료구조 및 프로그래밍] 16. O(N log N)정렬 방법 별 비교 횟수, 쓰기 횟수 비교 (0) | 2023.12.11 |
|---|---|
| [자료구조 및 프로그래밍] 15. O(N²)정렬 방법 별 비교 횟수, 쓰기 횟수 비교 (0) | 2023.12.10 |
| [자료구조 및 프로그래밍] 14. 정렬 (선택정렬, 삽입정렬, 퀵소트, 머지소트, 기수정렬) (0) | 2023.12.09 |
| [자료구조 및 프로그래밍] 13. Binary Search & Sequential Search (0) | 2023.12.05 |
| [자료구조 및 프로그래밍] 12. Hashing & Hash Table (0) | 2023.12.02 |
