Load Constant
MIPS에서 32bit 상수를 레지스터로 읽어올 때 2가지 방법이 있다.
첫번째는 메모리에 32bit 상수를 저장한 뒤, lw 명령어로 읽어오는 방법이다.
두번째는 lui, ori 2개의 instruction을 사용하여 읽어오는 방식이다.
lui 명령어는 load upper immediate 의 줄임말로, immediate 필드에 있는 16bit 상수를 레지스터의 상위 16bit에 저장하는 명령어이다.
그리고 나머지 하위 16bit 의 상수는 ori 명령어로 bit combine 하여 가져온다.

위 이미지와 같이 1234 를 상위 16bit에 쓰고, 5678을 하위 16bit에 쓰도록 해서 원하는 32bit 크기의 상수를 레지스터에 저장할 수 있다.
Pseudo Instructions
슈도 명령어는 기존 명령어들의 조합으로 실행해야하는 1가지 기능을 명령어 하나로 실행할 수 있도록 만든 일종의 alias 이다. 기존 ISA 에 없는 가짜 명령어인 셈이다.
가령 32bit 크기의 상수를 레지스터에 쓰고 싶을 때, 위 처럼 2가지 명령어를 혼합하여 사용할 수도 있지만, MIPS가 제공하는 li (load immediate) 명령어를 사용하면 명령어 하나로 상수값을 레지스터에 쓸 수 있다.
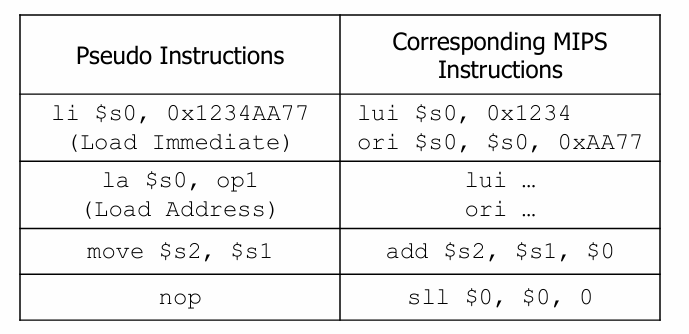
위는 MIPS 의 슈도 명령어 중 일부와, 이 명령어에 대한 실제 ISA 명령어 변환 결과이다.
(참고로 시험에 나오니 위 4개 슈도 명령어를 MIPS 명령어로 바꿀 줄 알아야 한다.)
Branch (분기)
지금까지는 명령어를 순차적으로 하나씩 실행했으나, 프로그래밍을 하다보면 특정 조건에 따라 서로 다른 명령어를 실행하거나, 명령어를 반복적으로 실행하고 싶을 수 있다.
이 말은 decision making 을 위해 PC 의 값이 4씩 증가하는 것이 아니라, 임의의 값으로 바뀔 수 있다는 말과 같다.
따라서 분기 명령어는 PC 값을 조작하는 명령어로 구성되어 있고, 종류에 따라 크게 조건 분기 (conditional branch, 무조건 분기 (unconditional branch) 로 나뉜다.
Conditional branch (조건 분기)
조건 분기는 말 그대로 조건을 확인하고, 조건에 따라 분기가 다르게 일어나는 것을 말한다.
조건 분기 명령어는 아래 2가지가 있다.
beq (branch if equal)
bne (branch if not equal)
조건 분기 명령어는 I-Format 이며 사용법은 아래와 같다.
beq/bne rs, rt, label
rs 레지스터 값과 rt 레지스터 값을 비교해서 같거나 다르면 label 위치로 분기한다.
label 은 해당 명령어가 위치한 메모리 상 주소를 갖고 있다.
이 값은 immediate 필드로 들어가는 상수값이고, 이 값의 의미는 '실제 주소' 가 아니라 현재 명령어 위치로부터 분기할 명령어 위치까지의 명령어 개수가 offset으로 들어간다.
각각의 명령어는 4byte 마다 저장되어 있으므로, 이 값을 통해 실제 이동할 주소를 계산할 때는 offset * 4 , 즉 왼쪽으로 2번 shift 한 값을 사용하게 된다.
또한 현재 명령어 위치의 실제 값은 PC + 4로 들어간다.
명령어를 가져오는 fetch cycle이 실행된 이후 pc 값은 4 증가하였기 때문이다.
따라서 정확하게 이 명령어는 PC + 4 위치를 base 로 하고, immdediate 필드에 들어있는 값을 2번 left shift 한 값을 offset 으로 해서 PC 값을 증가/감소 시키라는 의미가 된다.
이를 하드웨어에서 실제로 실행한다면, immediate 값을 sign-extension 시켜서 레지스터로 가져온 뒤, 왼쪽으로 2번 시프트 하고, PC+4 값과 더해서 새로운 PC 값으로 저장하는 과정으로 동작한다.
하지만 비교할 때는 '같다, 다르다' 같은 동등 비교 말고도, '크다, 작다, 크거나 같다, 작거나 같다' 와 같은 크기 비교도 필요하다.
이를 위해서 MIPS 는 slt 명령어를 제공한다.
이 명령어는 Set on Less Than 의 줄임말로, 두 수를 비교했을 때 더 작다면 레지스터의 값을 1로 세팅한다.
보통 $at 레지스터 (1번 레지스터) 를 세팅하는 용도로 사용한다.
slt 명령어는 R-Format 이다.
unsigned 값을 비교할 때는 stlu, 상수값과 비교할 때는 slti, 상수값과 unsigned 비교할 때는 sltiu 명령어를 사용한다.

포맷은 위와 같다.
이 명령어를 이용하면 크다, 작다, 크거나 같다, 작거나 같다 를 구현할 수 있다.
그리고 이에 대한 슈도 명령어도 blt, ble, bgt, bge 4가지 존재한다.
(이것도 시험에 나오니 4개 모두 slt 로 바꿀 수 있어야 한다.)

그리고 어셈블러가 슈도 명령어를 실제 명령어로 옮길 때는 $at 레지스터를 사용한다.
이 at 레지스터 (1번 레지스터) 의 값과, zero 레지스터의 값을 비교해서 분기 여부를 결정한다.
이 명령어들은 모두 signed 숫자에 대해 적용되며, unsigned 숫자에 대해 비교할 때는 bltu, bleu, bgtu, bgeu 를 대신 사용한다.
Bound Check
sign 넘버에 대해 bound를 체크할 때 sltu 를 이용하면 유용한 점이 있다.
예를 들어 어떤 수 x 가 0 이상 y 미만인지 체크해야 한다고 하자.
원래대로라면, x가 0 이상인지 비교 & x가 y미만인지 비교 이렇게 2번해야한다.
그런데 sltu를 이용하면 x가 0이상인지 비교할 필요가 없다.
만약 음수값이 들어오는 경우, MSB가 1이라서 unsigned로는 매우 큰 수로 인식되기 때문에 반드시 y보다 크기 때문이다.
따라서 sltu를 이용해 y보다 작다는 걸 확인하면 signed 넘버로는 0이상의 수라는 것도 동시에 만족하게 된다.
Unconditional branch (무조건 분기)
무조건 분기는 말 그대로 조건에 신경쓰지 않고 그냥 특정 위치로 분기하는 것을 말한다.
이를 jump 라고 해서 무조건 분기 명령어는 아래와 같은 종류가 있다.
j (jump)
jump 명령어는 J-Format 이라는 새로운 형태의 포맷을 사용한다.
J - Format은 opcode 6 bit, jump target 26 bit 2개 필드로 구성된다.
j 명령어의 포맷은 다음과 같다.
j target
j LLL 이라고 하면, LLL 이라고 하는 레이블로 무조건 분기를 시킨다.
레이블은 어떤 명령어에 붙인 일종의 태그이다.
LLL 이라는 레이블(태그) 가 붙은 명령어의 32bit 위치 정보는 26 bit로 다음과 같이 표현한다.
1. 현재 PC + 4 에 저장된 주소 값의 최상위 4개 bit를 jump할 명령어의 최상위 4개 bit로 사용한다.
(32bit 중 4bit 값을 정했으니 28bit가 남았다.)
2. branch 명령어와 비슷하게 26 bit 정보를 offset (명령어 수) 로 생각한 뒤, 2bit를 left shift 해서 나머지 하위 28 bit 를 결정한다.
즉, 점프할 목적지의 메모리 주소 32bit는 (PC + 4 의 최상위 4개 bit) + (26bit offset) + ( 00 = 명령어 offset을 바이트 주소로 변환하기 위해 left shfit 2번) 으로 계산한다.
branch 명령어에서의 레이블은 16bit 상수값의 오프셋이었다.
따라서 PC + 4 를 기준으로 앞 뒤 16bit 범위의 명령어로 분기할 수 있었다. (대략 앞 뒤로 각 32000개 명령어)
이 범위를 벗어난 범위로의 분기는 명령어 구조상 한번에 할 수 없다.
그런데 j 명령어는 PC + 4 를 기준으로 더하기 빼기를 하는게 아니라, 이 자체를 이용해서 주소값으로 즉시 활용하게 된다.
32bit로 표현할 수 있는 메모리 주소의 가짓수는 2^32 개, 따라서 최대 메모리의 크기는 2^32 byte = 4GB 이다.
J 포맷은 PC + 4의 상위 4개 bit 를 일단 가져다가 사용한다.
이 말의 뜻은, 메모리의 구역을 16등분으로 나눈 뒤, PC + 4 가 속한 그 구역 (256MB의 공간) 안에서만 점프한다는 의미와 같다.
이때의 점프할 수 있는 범위는 명령어 개수 기준으로 6400만 개 이다.
즉, branch 명령어보다 훨씬 넓은 범위에서 점프가 가능하다.
(그러다면 마침 PC + 4가 구역의 경계에 위치하고 있어서, 점프하려는 공간이 인접한 구역, 또는 타 구역에 있다면 어떻게 점프할 수 있을까?)
-> J-format은 그 범위가 PC + 4 기준 양쪽으로 공평하지 않은 것이 문제긴 한데, 그럼에도 불구하고 커버하는 범위가 워낙 넓어서 branch보다 더 파워풀하다고 볼 수 있다.
만약 branch 명령어를 이용해서 64000 범위보다 더 바깥 범위로 분기하고 싶다면 MIPS는 내부적으로 점프 명령어를 이용해서 분기한다.

예제를 보면, 두 레지스터의 값이 같으면 L1 으로 분기하려고 하는데, L1이 너무 멀리 있는 상황이다.
이때는 L1으로 분기할 수 있도록 jump 명령어를 branch 명령어 직후에 사용하고, 만약 두 레지스터의 값이 다르다면 L1으로 점프하지 않도록 L2라는 레이블로 분기하도록 어셈블러가 코드를 바꿔준다.
j 명령어 예제
다음과 같은 while 문 C코드를 어셈블리로 바꿔보자.
int pow = 1;
int x = 0;
while (pow != 128) {
pow = pow * 2;
x = x + 1;
}
128 보다 작은 동안 2를 계속 곱해내가고, x에는 그 횟수를 저장하는 반복문 코드다.
# x = s0
# pow = s1
move $s0, $zero
addi $s1, $zero, 1
addi $t0, $zero, 128
# Loop
LOOP:
beq $s1, $t0, BREAK
nop
sll $s1, 1
addi $s0, $s0, 1
j LOOP
nop
BREAK:나는 이렇게 작성해봤다.
sll 에 적는 상수값은 '시프트 횟수' 이지, 곱하는 값이 아님에 유의해야겠다.
# $s0 = pow, $s1 = x
addi $s0, $0, 1 # $s0 <- 1
add $s1, $0, $0 # $s1 <- 0
addi %t0, $0, 128 # $t0 <- 128
while:
beq $s0, $t0, done
sll $s0, $s0, 1
addi $s1, $s1, 1
j while
done:
강의록에는 위와 같이 작성되어 있었다.
이번엔 for 문을 바꿔보자.
int sum = 0;
int i;
for (i =0; i != 10; i = i+1) {
sum = sum + i;
}
나는 아래와 같이 바꿔보았다.
# sum = $s0, i = $s1
addi $s0, $0, 1
addi $s1, $0, 0
addi $t0, $0, 10
for:
beq $s1, $t0, done
nop
add $s0, $s0, $s1
addi $s1, $s1, 1
j for
done:강의록 코드를 보니 s0, s1 의 매칭만 거꾸로하고 똑같았다.
다음은 다른 for 문을 바꿔보자.
int sum = 0;
int i;
for (i = 1; i < 101; i = i*2) {
sum = sum + i;
}
아까와 비슷한데, 이번엔 i 가 매번 2씩 곱해진다.
# $s0 = sum, $s1 = i
addi $s0, $0, 0
addi $s1, $0, 1
addi $t0, $0, 101
for:
slt $at, $s1, $t0 # i < 101 이면 $at 이 1로 설정됨
beq $at, $0, done
nop
add $s0, $s0, $s1
sll $s1, $s1, 1
j for
done:
나는 위와 같이 작성했다.
jal (jump and link)
jal 명령어는 함수(프로시저)와 관련된 명령어이다.
함수는 실행이 끝나면 다시 호출했던 위치로 돌아와야 하는 구조이다.
따라서 프로그램 카운터의 값이 순차흐름이 아닌 방향으로 바뀌기 때문에 분기라고 볼 수 있다.
함수에는 매개변수 (파라미터, 또는 아규먼트) 가 있을 수도 없을 수도 있다.
매개변수에 값을 넘길 때는 매개변수에 넘기는 파라미터가 어딘가에 저장이 되어있어야 된다.
MIPS 는 최대 4개의 매개변수를 레지스터에 저장할 수 있도록 디자인하였으며, $a0 ~ $a3 레지스터를 사용한다.
함수를 호출한다는 말은 프로그램의 제어권이 메인함수에서 이 함수로 잠시 넘어간다는 뜻이기도 하다.
caller (함수를 호출하는 쪽) 이 가진 제어권을 callee (호출되는 함수) 에게 넘겨주는 것이다.
호출된 함수는 테스크를 수행한 뒤, 결과물을 return 한다. (물론 반환값은 없을 수도 있다.)
이 경우에도 return 값은 어딘가에 저장되어 있어야 한다.
그래야 caller가 이 반환값을 활용할 수 있다.
MIPS는 반환값을 $v0, $v1 두 개의 레지스터를 활용해 저장한다.
만약 곱셈 기능을 수행하는 함수라면 2word (64bit) 크기의 공간이 필요하기 때문에 2개 레지스터를 할당한다.
마지막으로 함수가 호출된 이후에는, 함수를 호출했던 코드의 다음 줄 코드가 실행된다.
이를 위해 다시 돌아갈 함수가 호출되었던 메모리 주소를 어딘가에 저장하고 있어야 하는데, 이 값은 $ra 레지스터에 저장한다. (순서상으로 제일 마지막 31번 레지스터이다.)
다시 jal 명령어로 돌아와서, jal 명령어는 jump and link 의 줄임말로, 점프도 하고 링크도 한다.
(엄밀히는 링크를 먼저하고 = 다시 돌아올 주소를 ra 레지스터에 저장하고, 점프한다.)
다시 돌아올 주소는 PC + 4 이다. 함수 호출 이후 그 다음 줄 명령어부터 실행하기 때문이다.
(사실은 nop 까지 고려해서 PC + 8 이 맞다.)
jal 명령어는 J Format 으로 j 명령어와 동일하게, 점프할 곳의 레이블을 바로 적으면 된다.
jal Label
jr (jump return)
jr 명령어는 ra 레지스터에 저장된 위치로 돌아가는 명령어로 R Format 이다.
ra로 돌아갈 때 사용하긴 하지만 돌아갈 레지스터를 정확히 명시해야 한다.
레지스터 번호는 5bit 이므로 op code 6bit, function 6bit, rs register 5bit 해서 17bit 만 사용한다.
보통 jr $ra 와 같이 사용한다.
함수 호출시 발생할 수 있는 문제
spilling register
메인함수에서 t 레지스터를 사용하고 있었는데, 함수를 호출하면서 레지스터의 공간이 모자라 t 레지스터를 사용하면서 기존 t레지스터 값을 잃는 경우이다.
이렇게 레지스터의 개수제한으로 레지스터의 값이 훼손되는 것을 register corruption 이라고 한다.
이 문제를 해결하기 위해서는 데이터를 레지스터가 아닌 다른 공간에 저장할 필요가 있다.
이렇게 레지스터의 내용을 다른 공간에 백업하는 것을 register spilling 이라고 한다.
레지스터를 백업하는 공간은 '메모리' 를 활용한다.
이때 사용하는 메모리 영역이 '스택' 영역이다. (LIFO, 라이포)
스택 영역은 다른 자료구조와 상충되는 것을 방지하기 위해 일반적으로 높은 주소에서 낮은 주소 방향으로 데이터를 넣도록 컨벤션이 정해져있다.
따라서 스택에서 값을 뺄 때는 낮은 주소부터 읽는다.
우선 스택 메모리 공간을 할당할 때는 $sp 라는 스택 포인터 레지스터의 주소값을 원하는 사이즈만큼 감소시켜서 할당한다. (스택 메모리는 높은 주소에서 낮은 주소로 감소하는 방향으로 할당되므로, 주소값을 감소시켜야 한다.)
다시 스택 메모리 공간을 돌려줄 때는 $sp 라는 스택 포인터 레지스터의 주소값을 할당했던 사이즈만큼 증가시키면 된다.
이 스택 포인터는 29번 레지스터로, 스택의 맨 위, top of the stack 의 주소값을 가리킨다.
다시 함수 호출 이야기로 돌아와서, 함수를 호출할 때 함수에서 사용할 레지스터의 기존 값을 훼손하기 싫다면 새로 스택을 할당한 뒤, 스택 영역에 기존 레지스터값을 백업해두고, 함수 내에서 레지스터를 자유롭게 조작하다가 함수 호출이 끝난 뒤, 스택에 백업해둔 값을 가져와 레지스터에 돌려주고, 스택 포인터를 증가시킨 다음 리턴 주소로 돌아간다.
하지만 매번 이렇게 수동으로 값을 백업하는 것은 귀찮은 일이다.
그래서 MIPS 는 preserved register, non-preserved register로 레지스터의 카테고리를 분류해두었다.
preserved register는 아래 레지스터가 해당된다.
- s 레지스터 (시험에 나옴)
- ra 레지스터
- sp 레지스터
- stack above sp 레지스터
이 레지스터들은 호출된 함수에서 그 값을 보존할 책임이 있다.
non-preserved register 는 아래 레지스터가 해당된다.
- t 레지스터
- a 레지스터
- v 레지스터
- stack below sp 레지스터
이 레지스터들은 호출하는 함수에서 그 값을 보존할 책임이 있다.
t 레지스터는 임시변수이기 때문에 callee 가 마음대로 바꿀 수 있다.
따라서 함수를 호출하기 전에 caller가 직접 백업해야 한다.
만약 t 레지스터값이 훼손되어서 caller 내부에서 문제가 발생한다면 이건 caller가 백업하지 않은 책임이다.
따라서 중요한 값은 t레지스터가 아니라 s레지스터에 저장하고, s레지스터가 모자라다면 caller가 직접 스택을 할당해서 메모리에 저장해둬야 한다.
하지만 s 레지스터는 임시변수가 아니라 caller 가 사용하는 변수이다.
따라서 callee 는 이 변수값을 바꾸는 경우, 자신이 직접 기존값을 백업해서 보존할 책임이 있다.
중첩된 함수 호출
함수중에서 다른 함수를 호출하지 않는 함수를 리프 프로시저 (leaf procedure) 라고 한다.
만약 메인함수에서 A 라는 함수를 호출하면서 매개변수도 넘기고 ra 에 돌아올 주소도 세팅해두었다고 하자.
그런데 A 라는 함수 내에서 B 라는 함수를 또 호출한다고 하자.
그러면 B 함수를 호출할 때 넘길 매개변수, 돌아올 주소값 ra 가 변경될 필요가 있다.
하지만 기존에 저장했던 값을 훼손할 수는 없다.
따라서 이 값들을 모두 스택에 백업해야한다. (호출된 함수, callee가 백업하여 보존할 책임이 있다.)
특히 같은 함수가 자신을 호출하는 것을 재귀 함수라고 한다.
int fact (int n) {
if (n <= 1) return 1;
else return n * fact(n-1);
}그 예제로 팩토리얼 계산하는 위 C 코드를 어셈블리로 옮겨보자.
fact: addi $sp, $sp, -8 # 8 byte 공간 확보 ($a0, $ra 백업)
sw $a0, 0($sp) # backup
sw $ra, 4($sp) # backup
# 함수 코드
lw $a0, 0($sp) # restore
sw $ra, 4($sp) # restore
addi $sp, $sp, 8 # 8 byte 공간 반환우선 함수를 실행할 때, register spilling 을 위해 스택 공간을 할당한다.
함수가 끝나면 할당한 스택 공간을 반환해주어야 한다.
함수가 처음 실행되면, 제일 먼저 argument 로 들어온 n 값이 1 이하인지 확인한다.
1이하면 바로 1을 반환한다.
fact: addi $sp, $sp, -8 # 8 byte 공간 확보 ($a0, $ra 백업)
sw $a0, 0($sp) # backup
sw $ra, 4($sp) # backup
# 함수 코드
addi $t0, $0, 1 # t0 = 1
bgt $a0, $t0, else # a0 > 1 then goto else
addi $v0, $0, 1 # v0 = 1
addi $sp, $sp, 8 # 함수 호출을 안했으니 백업했던 값은 필요가 없다.
jr $ra # return
else:
lw $a0, 0($sp) # restore
lw $ra, 4($sp) # restore
addi $sp, $sp, 8 # 8 byte 공간 반환else로 가는게 아니라면 그냥 1을 v0에 반환값으로 세팅하고, 반환하면 된다.
만약 else로 간다면 다시 재귀적으로 함수를 호출해야 한다.
fact: addi $sp, $sp, -8 # 8 byte 공간 확보 ($a0, $ra 백업)
sw $a0, 0($sp) # backup
sw $ra, 4($sp) # backup
# 함수 코드
addi $t0, $0, 1 # t0 = 1
bgt $a0, $t0, else # a0 > 1 then goto else
addi $v0, $0, 1 # v0 = 1
addi $sp, $sp, 8 # 함수 호출을 안했으니 백업했던 값은 필요가 없다.
jr $ra # return
else: addi $a0, $a0, -1 # n-1
jal fact
lw $a0, 0($sp) # restore
lw $ra, 4($sp) # restore
addi $sp, $sp, 8 # 8 byte 공간 반환
mul $v0, $a0, $v0 # return = n * fact(n-1)
jr $ra위와 같이 함수를 완성할 수 있다.
'CS > 컴퓨터 구조' 카테고리의 다른 글
| [컴퓨터 구조] 8. Computer Performance (0) | 2024.04.16 |
|---|---|
| [컴퓨터 구조] 7. MIPS 명령어 총 정리 (0) | 2024.04.16 |
| [컴퓨터 구조] 5. MIPS Data Transfer Instructions (2) (0) | 2024.04.14 |
| [컴퓨터 구조] 4. MIPS Data Transfer Instructions (1) (0) | 2024.04.06 |
| [컴퓨터 구조] 3. MIPS Arithmetic & Logical Instruction (0) | 2024.04.06 |
