지난 글에서는 뉴럴 네트워크와 역전파에 대해 정리하였다.

뉴럴 네트워크는 기계학습에서 학습시키는 함수의 새로운 형태로, 여러 단위 함수의 중첩함수 형태이다.
뉴럴 네트워크를 학습시킬 때도 로스를 구해서 로스의 값이 줄어드는 방향으로 학습시키게 되는데, 경사하강법을 사용하는 경우 미분 값이 필요하다.
여러 함수들이 합성된 뉴럴 네트워크에서 미분값을 구하기 위해, 데이터를 넣어서 전체 값을 계산하는 추론 과정과, 해당 값을 이용해서 각 레이어의 미분값을 구하는 학습 과정이 일어난다.
학습 과정에서는 역전파를 통해 각 레이어의 미분값을 구해두고, 업데이트 하려는 값에 대해서만 미분값을 활용하여 경사하강법과 같은 방식으로 다음 w 값을 업데이트 한다.
이번 글에서는 CNN 에 대해서 정리해보려고 한다.
사실 딥러닝 이라는 말은 뉴럴 네트워크와 똑같다.
과거에 처음 뉴럴 네트워크가 나왔을 때 단순한 엠니스트 데이터 셋에 대해서만 동작하고 조금 복잡한 데이터는 처리를 못했기 때문에 인식이 안 좋아서 제프 힌튼 교수가 새로 '딥러닝' 이라는 이름으로 리브랜딩했다고 한다.
역전파 기법의 등장으로 뉴럴 네트워크를 학습시키는 방법을 알게 되고, 레이어를 많이 쌓을 수록 그 성능이 올라간다는 것을 알게 된 후로, 많은 사람들이 딥러닝 기법을 연구하기 시작했다.

그리고 연구하면서 Convolutional layer, Pool layer, Fully connected layer, softmax layer 이렇게 4가지 종류의 레이어만 잘 조합해도 괜찮은 성능의 모델을 만들 수 있다는 것을 알게 되었다.
위 그림에서 사람 이미지를 기반으로 이미지를 분류하는 과정을 보면 Conv, Pool, FC, Softmax 레이어들의 조합을 통과해서 결과를 내는 것을 알 수 있다.
이제 각각의 레이어가 무슨 역할을 하는지 정리해보자.
Fully connected layer (FC)

FC 레이어는 위 그림과 같이 M x N x P 크기의 행렬을 받아서 Q x 1 벡터로 바꿔주는 레이어이다.
예를 들어 M x N 크기의 채널 (RGB 같은 것)이 P인 이미지가 FC 레이어를 통과하면 행렬을 쭉 펼쳐서 (M x N x P) x 1 크기의 벡터로 변환한다. 그리고 그 앞에 Q x (M x N x P) 크기의 행렬 W를 곱해서 Q x 1 크기의 벡터로 바꿔준다.
(출력 크기 Q는 우리가 정해준다.)
이때 FC 레이어에서는 Q x (M x N x P) 크기의 행렬 W가 학습 파라미터가 된다.

이미지 관점에서 FC 레이어의 의미를 살펴보면,
이미지의 크기가 200 x 200 이라고 하면, 우선 이미지 벡터를 펼쳐서 40000 x 1 크기의 벡터로 만들 수 있다.
그리고 FC 레이어의 출력값은 임의로 정할 수 있지만, 입력과 똑같이 40000 이라고 해보자.
그러면 입력과 출력을 매핑하는 행렬은 4만 x 4만 = 16억개의 파라미터를 가진다.
Convolution Layer
FC 레이어 하나에 대해 16억개 파라미터를 학습시키는 것은 현재 기술로는 불가능하다.
규모가 너무 커서 연산도 오래 걸리고, 이렇게 큰 파라미터를 학습시키려면 그만큼 많은 데이터가 필요하기 때문이다.
그래서 FC 레이어는 나중에 데이터 크기를 줄이고 나서 붙는 경우가 많다.
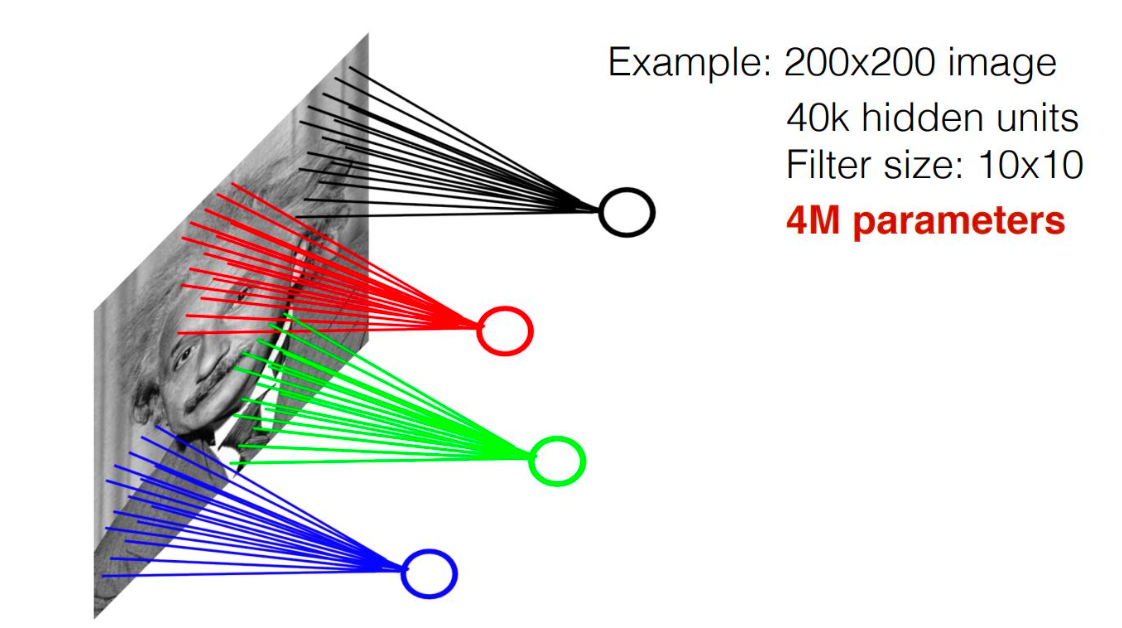
또는 이렇게 필터를 두기도 한다.
파라미터 수를 줄이기 위해 전체를 전부 다 연결하지 않고, 출력값 하나가 이미지의 특정 부분만 연결되도록 하는 것이다.
그러면 이미지 입력 크기의 상관없이 출력이 4만이라면 4만개 출력 각각이 10x10 = 100 개 픽셀과 연결되므로 400만개의 파라미터를 학습시키면 된다.
하지만 이것도 여전히 너무 많다.
그래서 모든 local weight 를 공유하자는 아이디어가 나왔다.
즉, 10 x 10 크기의 w를 모든 위치에 대해 공유한다.
그러면 최종적으로 10 x 10 짜리 필터가 있어서 필터를 이미지 왼쪽 위 모서리에 대고 내적해서 출력값 1개 내보내고, 옆으로 한칸 이동시켜서 출력값 구하고, ... 를 이미지 전체에 대해 반복하여 출력을 구할 수 있다.
이렇게 만들어진 출력값을 가리켜 Convolution 이라고 부른다.
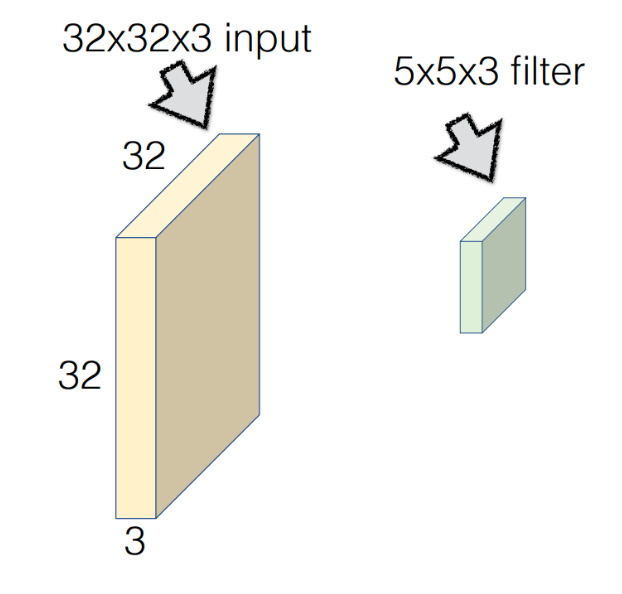
만약 이미지의 크기가 32 x 32 x 3 이고, 필터의 크기가 5 x 5 x 3 이라고 해보자.
(채널(또는 depth)은 3으로 보통 입력과 똑같이 맞춘다.)

이 필터가 왼쪽 위 모서리부터 쓸고 지나가면서 이동하면 이렇게 28 x 28 x 1 크기의 행렬이 만들어진다.
(이 행렬이 convolution 이다.)

기본적으로 쓸고 지나가는 간격은 1칸씩 쓸고 지나가지만, 이 간격도 우리가 자유롭게 정할 수 있다.
이 간격을 stride 라고 부르며, stride = 3 인 경우엔 3칸씩 건너 뛰면서 쓸고 지나간다.

또 convolution 은 기본적으로 크기가 줄어들 수 밖에 없는 연산이다.
이때 크기를 유지하고 싶다면 원본 이미지에 대해 패딩값을 줄 수 있다.
물론 패딩값의 크기를 가로 / 세로를 다르게 주는 것도 가능하다.

그리고 Convolution Layer 에서는 이 5 x 5 x 3 크기의 필터가 학습 파라미터이다.
이렇게 두면 기존의 FC 레이어에서와 달리 학습할 파라미터의 수가 매우 많이 줄어든 것을 알 수 있다.
그리고 위 그림에서 보는 것처럼 필터를 여러개를 사용하여 출력값을 쌓을 수도 있다.
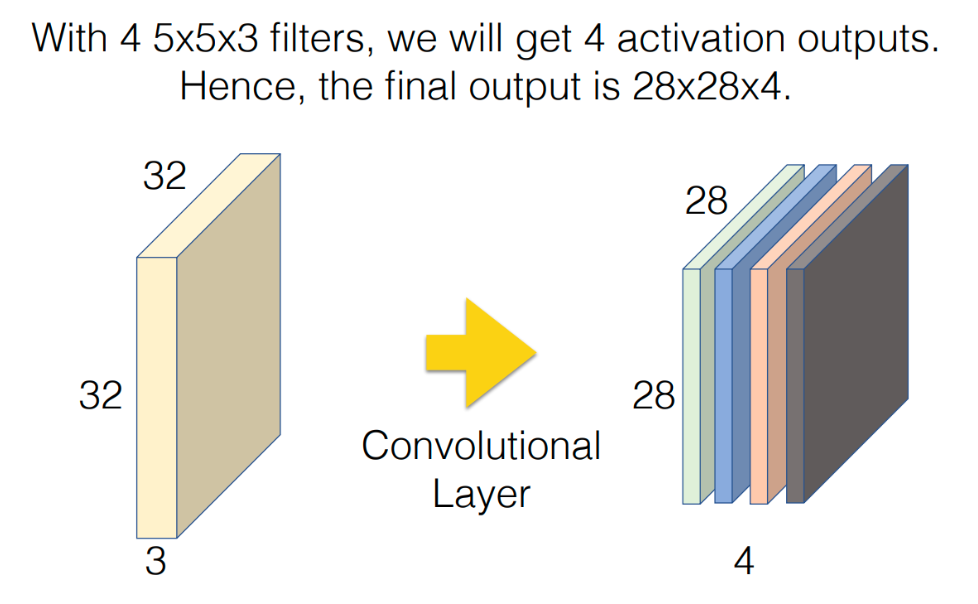
위 그림은 4개의 필터를 사용하여 28 x 28 x 4 크기의 Convolution Layer 를 만든 것을 볼 수 있다.
이때 필터의 크기, 스트라이드, 패딩같은 값들은 하이퍼파라미터로서 우리가 조정하는 값이고, 다만 필터의 채널 크기는 입력 데이터의 채널 크기와 맞춰준다.
그리고 필터 크기는 보통 홀수를 사용한다. (짝수를 사용하면 출력 크기가 홀수가 되고, 출력이 계속 홀수로 남게되면 크기를 나중에 맞추는 것이 힘들어서 보통 짝수로 유지되도록 홀수 크기 필터를 사용한다.)
결론적으로 위 그림과 같이 구성한 Convolution Layer의 학습 파라미터 개수는 5 x 5 x 3 x 4 = 300 개로 줄어든다.
Convolution Layer 를 사용하는 또 다른 이유는 성능과도 관련이 있다.
FC Layer 는 어떻게보면 필터를 이미지 크기와 똑같은 필터를 사용하는 것과 같다.
사람 얼굴을 인식해야 하는데, 첫 이미지와 두번째 이미지가 5픽셀 정도 평행이동한 이미지라고 하면, 첫 이미지로 학습해서 설정한 파라미터로는 두번째 이미지를 올바르게 인식할 수 없다.
반면 Convolution Layer는 여러 레어가 쌓여서 첫번째 레이어는 눈을 인식하고, 두번째 레이어는 코를 인식하고.. 하는 식으로 각각의 레이어의 역할을 나눠서 계산하기 때문에 잘 인식하게 된다.
첫번째 레이어 쪽에서는 필터가 눈을 지날 때 점수가 1에 가깝게 나오고, 눈이 아닌 곳을 지날 때는 점수가 안나올 것이고
두번째 레이어 쪽에서는 필터가 코를 지날 때 점수가 1에 가깝게 나오고, 코가 아닌 곳을 지날 때는 점수가 안나올 것이고
.. 이런식으로 4개 레이어를 사용한다고 하면 총 레이어 점수의 합이 4점 이상이면 얼굴로 본다와 같이 정의해서 얼굴을 인식할 수 있다.
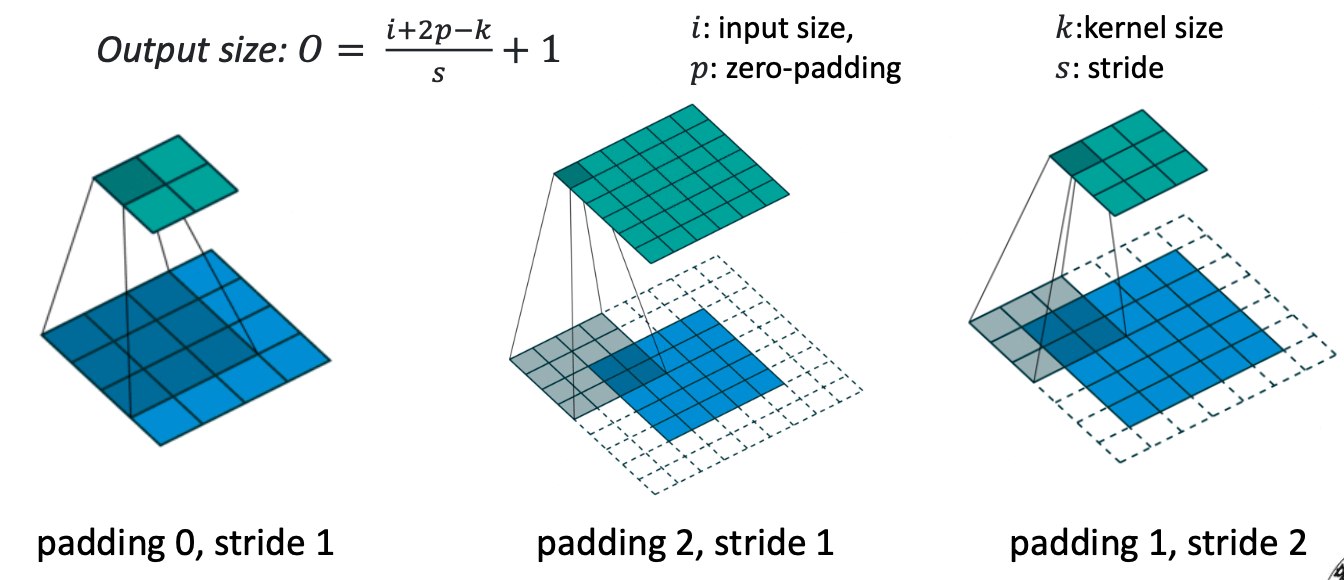
Convolution Layer 에서 필터 크기에 따른 output 행렬 크기는 위와 같이 계산할 수 있다.
위 식은 외워두는게 편하다고 한다..
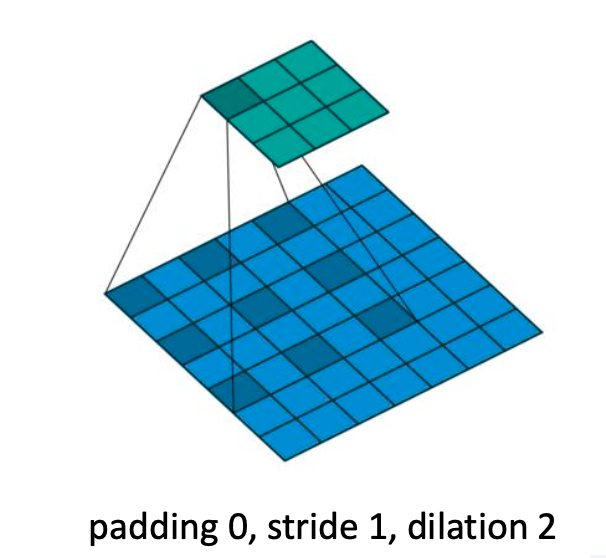
그 외에도 Dilation 이라는 개념이 있다.
이 개념은 3x3 필터라고 할 때 각 원소를 딱 붙여서 적용하는게 아니라 띄워서 적용하는 것을 말한다.
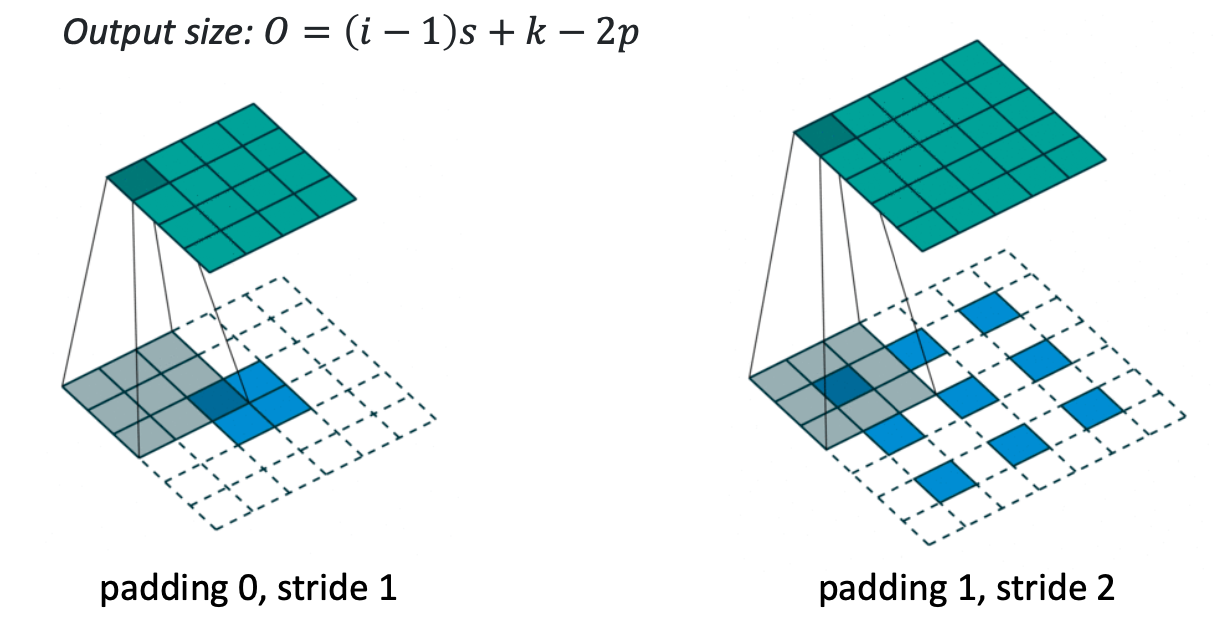
그리고 Transposed Convolution 이라고, convolution 을 거꾸로 적용한 레이어도 있다.
convolution은 기본적으로 크기가 줄어드는 연산인데, Transposed Convolution은 거꾸로 크기가 늘어난다.
패딩을 적용할 때도 원본에 패딩을 주었었다고 치고 연산한다.
convolution 연산을 완전 거꾸로 하는 것이라고 보면 된다.
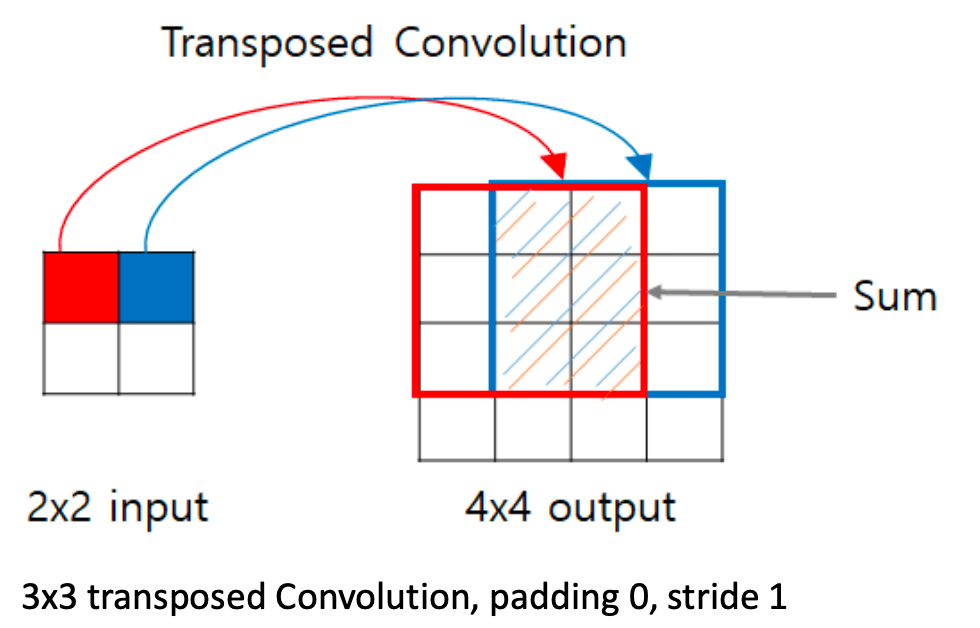
이때 크기가 늘어난 행렬의 값을 채울 때 겹치는 부분은 더해서 계산한다.
Max pooling layer
pooling 은 입력 데이터의 크기를 작게 만들어주는 레이어이다.
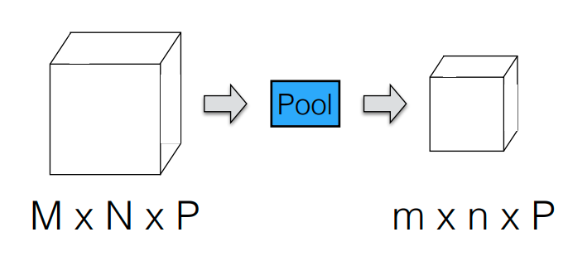
그래서 이렇게 M x N x P 크기의 데이터가 주어졌을 때 pooling layer 를 거치면 m x n x P 크기가 된다.
(채널 크기는 그대로 유지)
pool 도 convolution 과 비슷하게 필터를 사용한다.
이때 max pooling layer 는 필터에서 제일 큰 값을 취한다.

max pool layer의 목적은 딥러닝의 성능은 보전하면서 계산을 효율적으로 하는 것이다.
보통 max pool 을 사용할 때 필터의 크기는 2 x 2 필터에 stride = 2 를 주는 경우가 많다.
이렇게 하면 원본 이미지 크기에서 정확히 반으로 줄어든 이미지가 새로 나오게 된다.
이렇게 하면 원본 이미지가 열화되긴 하지만, 이미지가 갖고 있는 정보는 거의 유지되기 때문에 딥러닝 성능이 저하되지 않는다.
pooling layer 는 여러가지 있지만 max pooling 이 제일 흔하게 쓰이고, average pooling, L2-norm pooling 등도 존재한다.
pooling layer 를 두면 뒷 레이어의 파라미터 수를 줄이기 때문에 overfitting 을 막는 효과가 있다.
Softmax Layer
최종 output 데이터를 확률 기반의 클래스로 분류하는 레이어이다.

예를 들어 output 이 왼쪽과 같이 나왔을 때, 제일 큰 값인 7.2가 있는 쪽의 확률을 크게 키우고 나머지를 크게 낮춰서 타겟 데이터와 비슷하게 맞추는 것이다.
그런데 단순히 max 함수를 사용하기에는 그러면 이 함수가 미분가능하지 않아서 역전파를 사용할 수 없다는 문제가 있었다.
그래서 미분을 할 수 있도록 max 는 max 인데 부드러운 max를 적용하기 때문에 softmax 인 것이다.

우선 최종 결과가 확률이므로 각 원소의 크기는 0~1 사이의 값이며, 벡터 원소의 합은 1이어야 한다.
단순하게 각 벡터 원소값을 전체 합으로 나눠서 정규화를 해도 되지만, 이렇게 하면 큰 값의 비중을 더 크게 만들 수 없다.
그래서 이렇게 지수 함수에 zi (출력 벡터의 i 번째 원소)를 넣어 비율을 구한다.
원소의 값이 클 수록 e 라는 지수함수에서 매우 크게 작용하고, 원소의 값이 작으면 e 라는 지수함수에서 매우 작게 작용하기 때문에 비율을 구하면 큰 값의 영향력이 더 커지게 된다.
Loss function
이렇게 4가지 종류의 레이어를 조합하여 F(X) 를 만들고, softmax 까지 거쳐서 최종적으로 분류하는 모델을 만들었을 때, 이 모델을 학습시키기 위한 Loss 는 어떻게 구할 수 있을까?
Loss 를 구하는 방법 중에서 Cross Entropy Loss 가 있다. (L1, L2 로스를 사용해도 된다.)
이는 확률 분포를 비교하는 개념에서 유도된 loss 이다.

이 로스값은 위와 같은 함수를 통해 구할 수 있다.
확률이 기본적으로 0~1 사이의 값이기 때문에 log 를 취하면 - 부호가 나와서 -를 앞에 붙여주고,
i번째 true value 인 yi 를 곱해서 그 합을 구한다.
예를 들어보자.

이렇게 softmax 결과값과 True lable 이 있을 때, 위 공식에 이 값들을 넣어 loss 를 구해보면
true label = 0 인 곳은 0이 곱해지기 때문에 loss 에 영향이 없다.
따라서 -log(0.98) 이 loss 가 된다.
-log(0.98) = log(100/98) 이고, 이 값은 거의 log(1) 에 가깝다.
log 함수에서 log(1) = 0 이므로, 1에 가까울 수록 loss 는 0에 가까워지게 된다.
반면 예측에 틀리면 0과 멀어지고, log 함수 특성상 이 경우 loss 가 기하급수적으로 커지게 된다.
cross entropy loss 는 log를 사용하다보니 지수함수를 사용하는 softmax 와 주로 함께 다니는 경우가 많다.
Activation Function
지금까지 본 기본적인 뉴럴 네트워크는 linear 함수들의 합성으로 이루어졌다.
그런데 non-linenar 함수가 뉴럴 네트워크에서 굉장히 중요하다.

실제 뉴런을 보면 일정 역치 이상의 전기신호가 오지 않으면 그 신호를 전달하지 않는다.
뉴럴 네트워크에서도 이를 구현하기 위해, 역치와 비슷한 형태의 그래프를 그리는 함수를 적용할 수 있다.
(위 함수를 그대로 사용할 수 없는 것은 미분 불가능하기 때문이다.)

그래서 위 역치 그래프와 비슷하게 생긴 다음과 같은 그래프들을 사용한다.
처음에는 시그모이드 함수를 자주 사용했는데, 시그모이드 함수의 경우, 미분값이 0에 가까운 범위가 너무 많아서 역전파 연산시 방해가 되기 때문에 (vanishing gradient problem) 요즘은 ReLU 또는 Leaky ReLU 를 많이 사용한다고 한다.
다만 ReLU 와 같이 max() 함수를 사용하는 경우, x = 0 일 때 미분가능하지 않은데, 이때의 미분값은 0으로 두고 사용한다고 한다.
'CS > 기계학습심화' 카테고리의 다른 글
| [기계학습심화] 11. 딥러닝 (2) - Neural Network & Back Propagation (2) | 2025.04.21 |
|---|---|
| [기계학습심화] 10. 딥러닝 (1) - 선형 분류 모델 (2) | 2025.04.20 |
| [기계학습심화] 9. PCA (Principal Component Analysis) (3) | 2025.04.19 |
| [기계학습심화] 8. K-Means (0) | 2025.04.18 |
| [기계학습심화] 7. SVM (support vector machine) (1) | 2025.04.18 |
