지난 번에는 맥주축제를 제일 먼저 떠올랐던 이분탐색으로 풀어보았다.
이번에는 학습 목적에 맞게 우선순위 큐로 풀어보고자 한다.
우선순위 큐로 풀 때는 다음과 같은 알고리즘을 사용하였다.
1. 맥주를 도수가 낮은 순으로 우선 정렬하고나서 선호도 순으로 정렬한다.
2. 맥주가 있는 리스트를 돌면서 맥주를 하나씩 뽑는다.
2-1. 뽑은 맥주의 도수를 현재 도수로 한다.
2-2. 뽑은 맥주의 선호도를 우선순위 큐에 넣는다.
2-3. 우선순위 큐에 있는 선호도 합과 기준 합을 비교한다.
2-4-1. 기준 합보다 크거나 같다면 find변수를 True로 바꾸고 현재 도수를 출력한다.
2-4-2. 기준합보다 작다면 우선순위 큐에서 선호도가 가장 작은 원소를 pop한다.
3. 2번과정을 반복한다.
4. 만약 find변수가 false 라면 -1을 출력한다.
여기에서 개인적으로 중요하다고 느낀 것은
기준합보다 작을 경우, 도수를 신경쓰지 않고 선호도의 합 만을 고려하며 제일 작은 선호도를 제거한다는 것이다.
순간 "만약 직전에 넣은 맥주의 도수가 가장 높았는데, 하필 그 맥주의 선호도가 제일 작아
그 맥주의 선호도가 빠지게 되었다면 현재 뽑은 맥주들의 max 도수가 바뀔텐데 괜찮을까?"
라는 생각을 했었다.
다시 생각을 해보니 문제가 없었다. 처음에 맥주의 도수가 낮은 순으로 정렬을 했기 때문에
그 다음에 뽑을 맥주의 도수는 현재 뽑은 맥주의 max 도수보다 크거나 같음이 보장되어있기 때문이다.
이것을 파이썬으로 구현한 코드는 다음과 같다.
''' 맥주 축제 '''
import sys
import heapq
day, sum_taste, kind = map(int,input().split())
l = []
pq = []
heapq.heapify(pq)
for _ in range(kind):
taste, alch = map(int,sys.stdin.readline().split())
l.append((taste,alch))
l.sort(key=lambda x: (x[1],x[0]))
find = False
now_alchol = 0
s = 0
for i in range(kind):
heapq.heappush(pq,l[i][0])
s += l[i][0]
now_alchol = l[i][1]
if len(pq) == day:
if s >= sum_taste:
find = True
print(now_alchol)
break
else:
s -= heapq.heappop(pq)
if not find:
print(-1)처음에는 시간초과를 받았는데,
현재처럼 s 변수로 합을 관리하기보다 직관적이게
sum 함수를 사용했기 때문이다.
sum함수의 시간복잡도는 O(n)이니 당연한 결과였다..
sum함수는 가능하면 사용을 지양하는 것이 좋다는 점을 다시금 되새겼다.
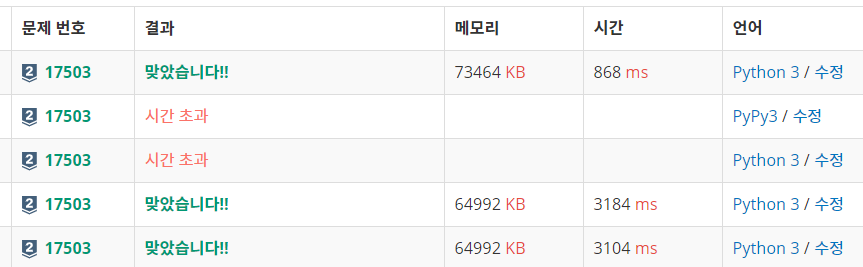
아래의 맞았습니다는 지난 포스팅에서 작성한 이분탐색 코드
위의 맞았습니다는 이번에 작성한 우선순위 큐 코드이다.
코드 길이도 매우 짧아졌지만, 시간차이가 확연히 난다.
'알고리즘 (PS) > BOJ' 카테고리의 다른 글
| [BOJ][Python3/PyPy3] 15553 - 난로 (0) | 2021.01.11 |
|---|---|
| [BOJ][Python3/PyPy3] 5639 - 이진 검색 트리 (0) | 2020.09.18 |
| [BOJ][Python3/PyPy3] 16681 - 등산 (다익스트라) (2) | 2020.09.01 |
| [BOJ][Python3/PyPy3] 17503 - 맥주축제 (이분탐색, 그리디) (0) | 2020.08.27 |
| [BOJ][Python3/PyPy3] 15811 - 복면산?! (0) | 2020.07.17 |
