교내 동아리에서 진행한 알고리즘 스터디의 마지막 수업으로 다익스트라를 배웠다.
연습 문제 중 이 문제가 개인적으로 막힌 부분이 많았고, 그로부터 배운 것들을 정리하고자 한다.
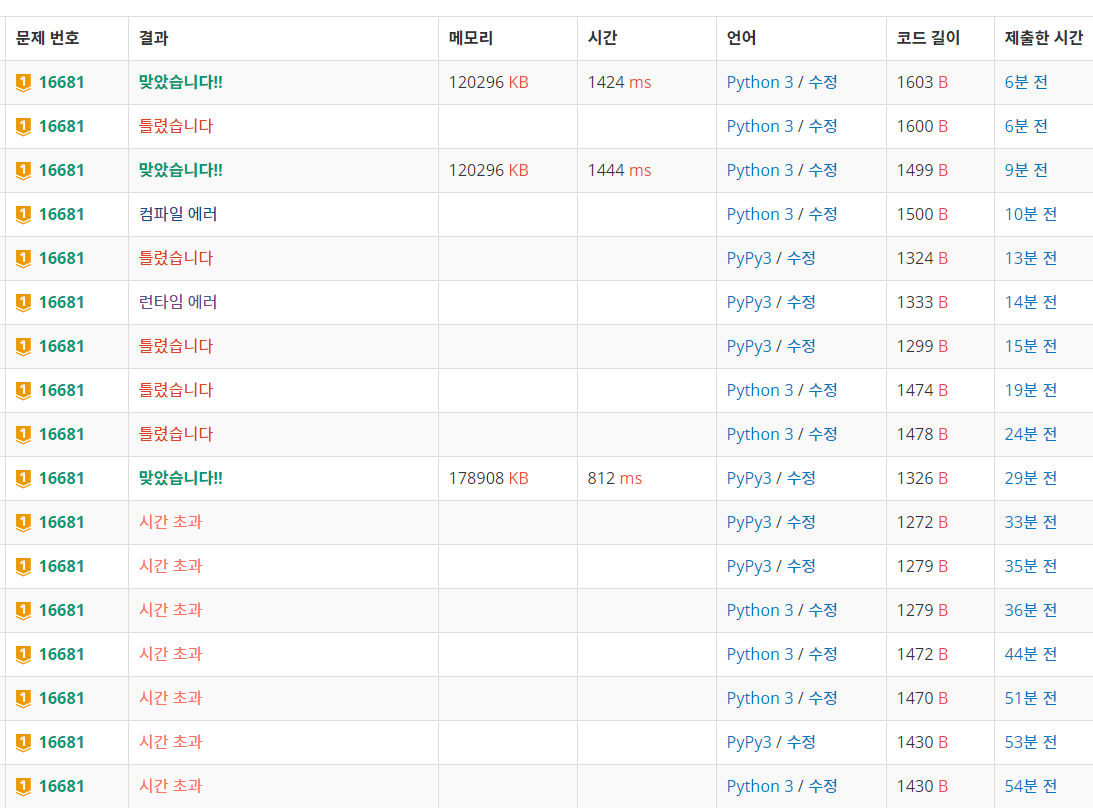
우선 이 문제를 풀기 위한 아이디어도 떠오르지 않았다.
결국엔 동아리 스터디 내용을 통해 아이디어를 얻고, 아이디어를 구현하여 제출하였다.
아이디어는 다음과 같다.
집에서 갈 수 있는 모든 산의 정상들
학교에서 갈 수 있는 모든 산의 정상들
이 두가지를 따로 구한다음 각각에서 구한 산의 정상의 교집합을 취하여 문제가 원하는 방식대로 계산하면 된다.
만약 교집합이 없다면, 답이 없다는 뜻.
나는 다익스트라를 구현하고, 다익스트라의 결과로 나온
집/학교에서 출발 했을 때 갈 수 있는 모든 산의 정상들 (노드) 번호, 각각의 노드로 가는 최단거리
이 두가지를 따로따로 구하여 저장하였다.
그 후 각각의 노드 번호들의 교집합을 취하고
그 교집합 내 원소들을 가지고 기대하는 결과값을 구한다음
결괏값의 최댓값을 갱신하는 과정을 반복하여 구하였다.
그러나 문제가 생겼다.
1. 시간 초과
처음에는 왜 시간초과가 나는지 알 수 없었다.
정답코드를 대충 보았다.
나는 집합을 사용했지만, 정답코드는 집합을 쓰지 않고 구했다.
그래서 나도 집합을 쓰지 않도록 해보았으나 여전히 시간초과였다.
그 원인은 다익스트라 구현과정에서 있었다.
def dijkstra(node):
global n
INF = 9876543210
short = [INF]*(n+1)
short[node] = 0
pq = []; heapq.heapify(pq)
heapq.heappush(pq, (short[node], node))
result = []
while pq:
c, pos = heapq.heappop(pq)
for p in path[pos]:
if height[p[0]-1] > height[pos-1]:
if c + p[1] < short[p[0]]:
short[p[0]] = c + p[1]
result.append(p[0])
heapq.heappush(pq, (short[p[0]], p[0]))
return result, short내가 작성한 다익스트라 코드이다.
난 지금까지 주어진 다익스트라 연습문제를 모두 이 코드의 구성으로 풀었고, 전부 아무 문제가 없었다.
그러나 이 문제에서는 이 코드로는 통과할 수가 없었다.
정답코드는 다음과 같았다.
def dijkstra(node):
global n
INF = 9876543210
short = [INF]*(n+1)
short[node] = 0
pq = []; heapq.heapify(pq)
heapq.heappush(pq, (short[node], node))
result = []
while pq:
c, pos = heapq.heappop(pq)
if short[pos] < c:
continue
for p in path[pos]:
if height[p[0]-1] > height[pos-1]:
if c + p[1] < short[p[0]]:
short[p[0]] = c + p[1]
result.append(p[0])
heapq.heappush(pq, (short[p[0]], p[0]))
return result, short차이점은 딱 하나
if short[pos] < c:
continue
while 문 중간에 이 코드가 있느냐 없느냐 차이였다.
현재 위치한 노드로 오는 최단거리가 힙에 들어있던 그 노드의 최단거리보다 짧다면 무시하는 것.
이 코드가 필요한 이유를 고민해보니 알 수 있었다.
내 노드로 오는 위치의 최단 거리는, 다른 노드에서의 갱신을 통해 바뀔 수 있다는 것.
예를 들어서
1번 노드의 방문 이후, 3번 노드로 오는 최단경로를 10으로,
2번 노드로 오는 최단 경로를 5로 갱신했다고 해보자
우선순위 큐에는 (5,2) , (10, 3) 이 들어있다.
이제 우선순위 큐에서 가장 짧은 경로를 뽑는다.
(5,2)가 될 것이고, 2번 노드에서 3번노드로 가는 최단경로가 1 이라고 해보자.
그렇다면 현재 3의 최단경로인 10 보다. 5 + 1 = 6 이 더 짧으므로
최단 경로는 (6, 3) 으로 갱신되며, 이 튜플이 PQ에 추가된다.
난 계속 '최단경로'를 구하는 것에 목적을 둔 나머지,
현재 순간의 최단 경로를 저장하는 배열 short의 갱신에만 집중하고 있었다.
내가 빼먹은 것은 PQ를 생각하지 않았다는 것이다.
위 예시에서 노드 3까지의 최단경로는 성공적으로 갱신되었다.
그러나 PQ에는 아직 (10, 3) 인 최단경로 10이었을 적의 데이터가 남아있다.
만약 저 continue 문을 뺀다면
이 10이라는 데이터에 대해 이 값을 최단 경로로 보고 노드3과 연결된
다른 노드들에 대해 반복문을 돌릴 것이다.
결과적으로 틀리지는 않는다.
언젠가 6으로 갱신된 최신의 데이터가 PQ에서 뽑힐 것이고,
그 값으로 반복문을 돌면 최단경로는 전부 갱신될테니까
대신 의미없는 작업을 하게 된다.
그래서 시간초과가 난 것이다.
이 문제를 통해서 내가 구현한 다익스트라 알고리즘의 허점을 하나 발견하고 채울 수 있었다.
2. 틀렸습니다.
분명히 시간초과는 해결했는데, 그럼에도 불구하고 틀렸습니다가 나왔다.
정답코드와 비교해봐도 다익스트라 알고리즘 자체의 문제는 아니었다.
그렇다면 메인 부분에서의 문제인데..
from_home, home_short = dijkstra(1)
from_school, school_short = dijkstra(n)
from_home = set(from_home).intersection(set(from_school))
answer = []
if from_home:
want = -9999999999
for conn in from_home:
want = max(want, height[conn-1]*a - (home_short[conn] + school_short[conn])*h)
print(want)
else:
print('Impossible')틀렸습니다를 받았던 코드의 메인 부분이다.
교집합 내 원소들에 대해 반복문을 돌면서
매 순간순간의 최댓값을 갱신하는 코드이다.
정답인 코드는 다음과 같았다.
home_short = dijkstra(1)
school_short = dijkstra(n)
answer = []
for i in range(1,n+1):
if home_short[i] != INF and school_short[i] != INF:
answer.append(height[i-1] * a - (home_short[i] + school_short[i]) * h)
print(max(answer) if answer else 'Impossible')정답인 코드는 집합을 사용하지 않고,
그냥 각각에 대해 최단경로 리스트를 따로 받은다음
동일 인덱스 값에 대해 둘다 경로가 존재한다면,
그 경로에 해당하는 결과값을 계산하고, answer 리스트에 삽입
최후에는 answer 리스트의 최댓값을 구하는 것이다.
교집합을 쓰느냐, 모든 리스트를 받아서 일일히 비교하느냐의 차이가 있고
정답 후보를 모두 저장하고, 거기서 max 를 구하느냐, 매 순간 순간의 max 를 구하느냐의 차이가 있다.
두가지 차이점 중 무엇이 문제인지 검증해보았다.
정답코드를 집합을 사용하되, 정답은 모두 모았다가 한번에 max를 구하도록 바꿔보았다.
=> AC를 받았다
그렇다면 집합을 쓰느냐, 두개 리스트를 놓고 비교하느냐는 문제가 아니다.
(따라서 틀렸던 코드에서 집합대신 리스트 비교를 써보게 하는 것은 의미가 없다.)
이번엔 정답코드의 답 도출방식을 매 순간 max 값을 구하도록 바꿔보았다.
=> WA 를 받았다.
여기가 문제였다.
그런데 이해가 되질 않았다.
정답을 모아놨다가 한번에 max값을 구하나, 매 순간 최적인 max값을 구하나 무슨 차이가 있는 걸까
결국 알아낸 원인은 다음과 같았다.
want = -9999999999
초기 want값은 다음과 같다.
그 말인 즉슨 모든 테스트 케이스에서 나올 수 있는 모든 결괏값이
적어도 이 값보다는 클것이라는 전제가 있었다.
그러나 그렇지 않았다.
결국
want = -9999999999999
정도로 want 값을 더 작게 설정하여 맞추었다.
이 문제를 통해 배운 점 두번째는
max, min 을 구하기 위해 비교할 기본 값을 어느정도로 작게 해야할 지 계산이 안되거나 감이 오지 않는다면
매 순간순간에서의 비교보다는 모든 답을 저장했다가 그 답들을 후보로 max min 을 구하는 것이 낫다는 점.
(물론 답들이 너무 많이 나와서 메모리 초과가 우려된다면, 매 순간에서 비교해야하겠지만 말이다)
또 하나 배운 점 세번째는
print 문에서도 리스트 축약같은 저 표현식을 쓸 수 있다는 걸 처음 알았다 ㅋㅋ
쓸데없는 파이썬 기교지식이 하나 추가되었다.
'알고리즘 (PS) > BOJ' 카테고리의 다른 글
| [BOJ][Python3/PyPy3] 15553 - 난로 (0) | 2021.01.11 |
|---|---|
| [BOJ][Python3/PyPy3] 5639 - 이진 검색 트리 (0) | 2020.09.18 |
| [BOJ][Python3/PyPy3] 17503 - 맥주축제 (우선순위큐, 그리디) (0) | 2020.08.29 |
| [BOJ][Python3/PyPy3] 17503 - 맥주축제 (이분탐색, 그리디) (0) | 2020.08.27 |
| [BOJ][Python3/PyPy3] 15811 - 복면산?! (0) | 2020.07.17 |
