Trnasformation
객체의 위치를 옮기거나 모습을 변형하는 것 (이동, 회전, 크기 변경)
변환을 할 때는 행렬을 사용하는 것이 효율적이다.
OpenGL 에서 사용할 때는 Shader 의 input vertex 를 변환하는 것으로 적용한다.
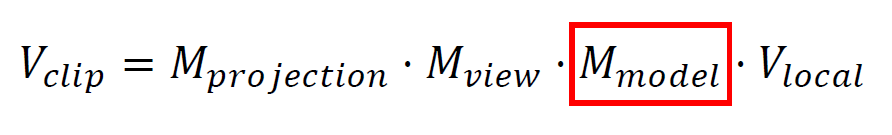
다음이 OpenGL 에서 사용하는 변환의 큰 과정이다.
대문자 V 는 vertex 정점을 의미하고, M 은 matrix 행렬을 의미한다.
V clip 이라는 정점을 얻기 위해 V local 이라는 정점에 model 행렬, view 행렬, projection 행렬 순으로 변환을 적용한다는 의미이다.

이를 OpenGL 방식 코드로 보면 이렇게 된다.
입력 정점으로 V local 이 들어오면, 여기에 model 행렬을 곱해 변환하고, view 행렬을 곱해 변환하고, projection 행렬까지 곱해서 최종 변환해 정점이 화면에 출력될 위치를 정하는 것이다.

이 그림을 보면 저 과정을 다 이해할 수 있다.
먼저 우리가 원하는 목표를 생각해보자.
우리의 목적은 이 세상에 존재하는 3차원 물체를 스크린에 사람이 보는 관점의 느낌으로 띄우려고 하는 것이다.
그러려면 먼저 3차원 물체를 3차원 좌표계로 묘사를 해야한다.
3차원 물체는 각자 자신을 중심으로한 좌표계를 기준으로 자신을 묘사하고 있다.
예를 들어 이미지의 정육면체의 한 가운데 중심이 (0, 0, 0) 이라고 하자
그러면 정육면체의 각 꼭짓점은 저 정육면체의 가운데 중심 원점 (0, 0, 0) 을 기준으로 위치값을 나타낼 수 있을 것이다.
여기에서 '정육면체' 를 가리켜 '모델' 이라고 하고, 정육면체가 자신을 구성하는 정점의 위치를 표현하기 위해 사용한 자신만의 좌표계를 '모델 좌표계' (Model Coordinate System) 이라고 한다.
하지만 실제 World 에는 정육면체 하나만 있는게 아니다.
위 이미지를 기준으로 한다면 정육면체도 있고, 사각뿔도 있다.
그리고 사각뿔도 하나의 모델로서, 자신의 형태 (자신을 구성하는 정점) 를 묘사할 때, 자신만의 모델 좌표계를 사용한다.
이때 실제 World에 이 모델들을 나타내는 각각의 정점 위치를 나타내려면 이들의 좌표계가 아닌 World의 좌표계를 사용하여 나타내야한다.
구체적인 숫자를 예시로 들어보자.
만약 정육면체의 꼭짓점 하나의 좌표를 나타낼 때, 정육면체 중심을 원점으로 하는 모델 좌표계를 기준으로 (1, 0, 0) 이었다고 해보자.
과연 이 (1, 0, 0) 이라는 좌표를 World 에 정육면체를 배치한 이후에도 그대로 사용할 수 있을까?
만약 정육면체의 중심을 world 좌표계의 (0, 0, 1000) 위치에 배치했다면, 정육면체 모델 좌표계 상에서 (1, 0, 0) 이었던 점의 world 좌표계 상 좌표값은 다르게 나올 것이다. (최소한 z 값에 뭔가 변화가 크게 있지 않을까?)
그래서 모델의 정점을 묘사하기 위해, 모델 좌표계를 기준으로 작성한 정점의 좌표값을, world 좌표계 기준으로 나타낸 좌표값으로 변환할 필요가 있다.
이때 사용하는 것이 Model Matrix 다.

위 수식 이미지에서 이 부분이 그 뜻이다.
vec4 는 Model Coordinate System (MCS) 위의 점이고, 이 점에 대해 model matrix를 적용하여 변환을 가하면 World Coordinate System (WCS) 위의 점으로 변환된다.

이제 View Matrix 부분을 보자.
세상 (world) 은 3차원 공간이다.
사람은 3차원 공간의 한쪽 면을 골라 바라보며, 그 면을 2차원으로서 인식한다.
이렇게 사람이 3차원 공간에서 바라보고 있는 방향을 '뷰' 라고 한다.
위 이미지에서도 자세히보면 '카메라' 가 위에서 아래로 바라보고 있는 것을 알 수 있다.
이렇게 3차원 공간을 2차원 공간으로 바라본 결과물을 알고 싶을 때 view matrix 를 사용한다.
위 이미지에서는 카메라가 녹색 축 위에서 바라보고 있으므로 아래와 같이 보일 것이다.

이렇게 보면 정육면체의 정점은 상단 꼭짓점 4개만 보이고,
사각뿔의 정점은 아래 4개, 윗 꼭짓점 1개의 5개 정점만 보인다.
그리고 이들의 좌표는 3차원이 아니라 2차원으로 묘사될 것이다.

그게 이 과정이다.
WCS (World Coordinate System) 상에서 정의된 정점에 view matrix를 곱해서 VCS (View Coordinate System) 으로 변환한다.
만약 카메라의 위치가 바뀌면, 카메라에서 보이는 scene도 똑같이 바뀌면서 2차원 영역에 찍히는 정점도 다르게 찍힐 것이다.
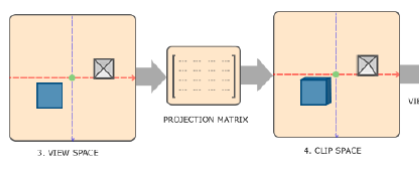
마지막 변환은 뷰에서 프로젝션을 하는 것이다.
프로젝션 (투사) 과정을 거치면 원근감이 부여된다.
또 카메라의 렌즈에 따라 왜곡이 들어가기도 하고, 광각이 되기도 하는 등 여러 필터 효과가 생길 수 있다.
이를 적용하는 것이 투사이다.
이렇게 투사까지 완료된 좌표계 공간을 CLIP Space 라고 한다.
그리고 이 Clip Space 위의 각 정점들을 V clip 으료 표현할 수 있다.

이제 이 수식을 다시보면 이해가 된다.
모델 좌표계를 기준으로 묘사된 정점에 대해 모델 행렬을 곱해 월드 좌표계상 점으로 바꿔주고, 여기에 뷰 행렬을 곱해 뷰 좌표계 상 점으로 바꿔준다. 여기에 투사 행렬을 곱해 클립 좌표계 상으로 정점으로 바꿔주는 것이다.
이렇게 하면 모델의 정점을 우리가 원하는 2차원 평면상 위의 점으로 표현하는 것은 끝났다.
하지만 한가지 과정이 더 남아있다.
이렇게 계산한 2차원 평면은 무한히 넓은 2차원 평면이다.
하지만 사람이 한번에 볼 수 있고, 컴퓨터가 모니터상에 한번에 띄울 수 있는 2차원 영역은 한정적이다.
이렇게 실제로 눈에 보여줄 2차원 영역을 ViewPort 라고 한다.

이 이미지의 마지막 단계가 CLIP SPACE 의 모습에서 일부 화면을 똑 따내서 뷰 포트를 적용하여 SCREEN SPACE 상 점으로 보여주는 모습이다.
이때는 Viewport Transfromation 이 적용된다.
직교 좌표계 vs 동차 좌표계
이제 지금까지 정리한 모델 변환 행렬, 뷰 변환 행렬, 투사 행렬을 만들기 위한 기초 변환 행렬을 알아보자.
행렬 변환을 정리하기 전에 좌표계에 대해 먼저 정리한다.
그래픽스에서는 힝렬 변환시 우리가 자주 사용하는 직교 좌표계 대신 동차 좌표계를 사용한다.
직교 좌표계
우리는 수학에서 직교 좌표계 (데카르트 좌표계) 를 주로 사용한다.
영어로는 orthogonal coordinate system 이라고 한다.
이 좌표계는 원점 위치와 축 방향, 축 눈금 간격을 이용해 특정 점의 위치를 표현한다.
또 같은 점이라도, 좌표계의 기준점에 의해 그 점의 위치를 나타내는 좌표값은 달라질 수 있다.
직교 좌표계는 벡터와도 관련이 있다.
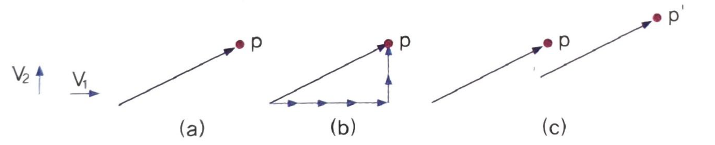
이렇게 어떤 점을 나타내는 벡터를 2개의 직교하는 벡터로 표현할 수 있다.
이 두 벡터를 기반 벡터 (basis vector) 라고 한다.
기반 벡터는 자기들 끼리는 서로 linearly independent 하다는 특징이 있다.
즉, 3차원 공간에서 서로 직교하는 벡터들은 서로 linearly independent 하다.
동차 좌표계
보통은 (나도 멀티미디어응용수학 배울 때) '호모지니어스 좌표계' 라고 부른다.
어떤 점을 나타낼 때, 그 점 좌표 마지막에 원소를 하나 추가한다.
0을 추가하면 벡터가 되고 (이건 잘 안쓴다), 1을 추가하면 점을 나타내게 된다.
보통 1을 추가해서 점으로 사용한다.
컴퓨터 그래픽스에서는 모든 좌표를 동차 좌표로 표시하며, 그래픽스 하드웨어도 이에 맞춰 한 번에 4개 요소 (3차원 위의 점은 4개 요소를 가지므로) 를 입력하고 처리할 수 있도록 설계한다.
동차 좌표계를 쓰면 행렬 연산 시 이점이 있다.
또 고차원에서 저차원으로 투사하는 projection 을 위해서 사용하는 것도 있다.
이동 변환 (Translational Transformation)
이동 변환은 물체를 직선 방향으로 이동하는 변환이다.
직교 좌표계라면 아래와 같이 작성할 수 있다.

하지만 그래픽스에서는 행렬 덧셈을 하지 않는다.
오직 행렬 곱셈만을 할 뿐니다.
이 이동변환을 행렬 곱셈으로 표현할 때 동차좌표계가 사용된다.

2차원 점은 이런 형태의 변환 행렬을 곱한다.
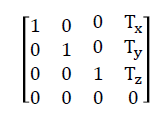
3차원 점이라면 이런 형태의 행렬을 곱한다.
이 행렬 오른쪽에 변환하기 전 정점을 (x, y, z, 1) 형태로 넣어 곱하면 그 결과로 (x + tx, y + ty, z + yz, 1) 형태의 이동된 정점이 나온다.
회전 변환 (Rotational Transformation)

파이만큼 회전된 위치에 존재하는 어떤 좌표를 추가적으로 세타만큼 회전했을 때, 그 위치가 위와 같은 공식으로 나타난다.

기하학적으로는 이렇게 된다.
3차원 회전의 경우, 축에 대해 회전한다면 2차원과 비슷하게 아래와 같이 나타낼 수 있다.
1. z 축 중심 회전
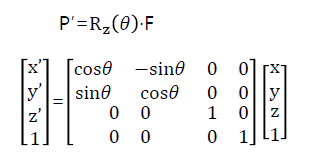
2. x 축 중심 회전
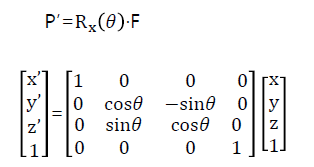
두 회전 모두, 회전하려는 축의 성분을 1로 놓고, 나머지 성분에 대해 c, -s, s, c 순으로 작성하면 된다.
3. y 축 중심 회전

y 축 중심 회전은 위와 같이 표현된다.
주의할 점은 c, s, -s, c 순으로 sin 함수의 부호가 x, z 와 서로 반대라는 것이다.
크기 변환 (Scaling Transformation)

위에 모든 내용이 기술되어 있다.
저 행렬을 곱해서 계산해보면 x' = Sx * x 와 같은 꼴로 각 성분이 계산된다.
만약 Sx, Sy, Sz 가 모두 같다면 균등 크기 조절, 하나라도 다르면 차등 크기 조절이라고 한다.
지금까지 행렬 변환에 대해 정리하였다.
다음 글에서는 각 변환들을 서로 복합적으로 섞어 사용하는 복합 변환에 대해 정리한다.
그리고 이 변환을 gl 에서 할 수 있는 수학 라이브러리인 glm 에 대해서도 정리한다.
'CS > HCI 윈도우즈프로그래밍' 카테고리의 다른 글
| [OpenGL] 15. Transformation (3) - GLM 사용하기 (0) | 2024.04.19 |
|---|---|
| [OpenGL] 14. Transformation (2) - 복합 변환 (0) | 2024.04.18 |
| [OpenGL] 12. Shader (8) - 여러 Texture 생성하기 (0) | 2024.04.14 |
| [OpenGL] 11. Shader (7) - Texture Wrapping, Filtering, MipMaps (1) | 2024.04.12 |
| [OpenGL] 10. Shader (6) - Texture (0) | 2024.04.11 |
