이제 지금까지 정리한 변환을 실제 코드로 구현해보려고 한다.
OpenGL 과 관련하여 행렬 연산을 간편하게 지원하는 glm 라이브러리를 사용하면 편하게 행렬을 만들고 연산할 수 있다.
GitHub - g-truc/glm: OpenGL Mathematics (GLM)
OpenGL Mathematics (GLM). Contribute to g-truc/glm development by creating an account on GitHub.
github.com
우선 위 깃허브에 가서 최신버전의 glm 을 다운받는다.
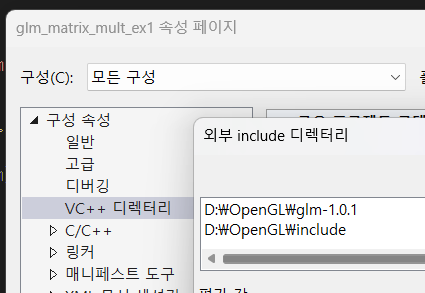
다운받은 glm 파일은 외부 include 디렉터리로 꼭 등록해주자.

이제 glm 을 사용하여 행렬연산을 할 수 있다.
이때는 위와 같은 헤더를 include 해주어야 한다.
우선 glm 을 사용하기전에 한 가지 주의할 점이 있다.
OpenGL 의 행렬은 column - major 방식으로 사용한다.

위 이미지에서 m[0] 은 0번째 '행' 이 아니라 0번째 '열' 을 의미한다.
내 개인적인 추측으로 이렇게 사용하는 이유는 1차원 배열을 열벡터로 사용하려고 하는 것 같다.
따라서 m[x][y] 라고 사용하면 x열 y 행의 데이터를 읽겠다는 의미이다.

위와 같이 선언하면 오른쪽 행렬로 인식된다고 한다.
보통 저렇게 사용하면 왼쪽부터 x, y, z, 1 순으로 읽는게 일반적이니까 위에서 아래로 내리듯 쓰는 걸 4번 반복한다고 생각하면 될 것 같다.
행렬 생성
이제 본격적으로 행렬을 사용해보자.
우선 glm에서 행렬 객체는 아래와 같이 선언한다.
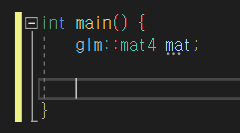
glm 네임스페이스 에정의된 mat4 클래스를 불러온다.
mat4는 4x4 행렬이다.
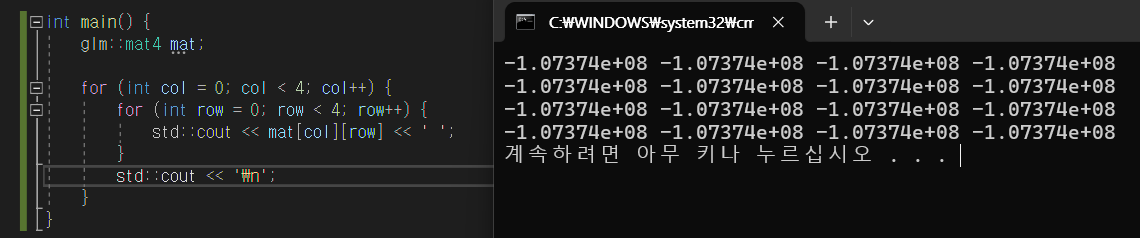
초기화를 안하고 출력하면 쓰레기 값이 들어있다.
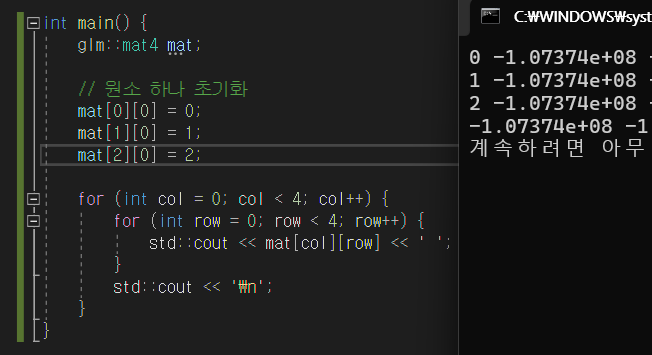
2차원 배열을 다루듯이 값을 수정할 수 있다.

지금을 출력을 저렇게 해서 그렇지 실제로는 위와 같이 col major 방식으로 동작할 것이다.

값을 초기화 하는 다른 방법으로, 하나의 열을 1차원 벡터를 이용해 한번에 초기화할 수도 있다.

마지막 열이 모두 3으로 초기화되었다.
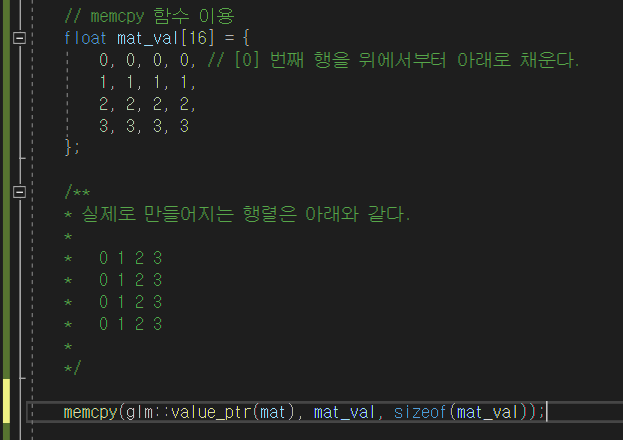
마지막으로 memcpy 함수를 이용해서 1차원 배열을 이용해 초기화 할 수도 있다.

실행결과 잘 채워졌다.
변환 행렬 생성
위의 내용은 임의 행렬을 직접 만드는 방법을 정리한 것이다.
Open GL에서는 Transport, Rotate, Scale 같은 기본 변환 행렬을 만드는 함수를 제공한다.
이런 기본 변환 행렬은 정해진 포맷이 있기 때문에 함수를 사용하는 것이 더 편하다.
이동 행렬
glm::translate() 함수를 이용한다.
변환할 4차원 행렬, 3차원 공간에서의 이동량을 vec3 형태로 넣으면 된다.

이렇게 단위행렬을 입력으로 주고, 이동 변환을 적용해보았다.
단위행렬은 아래와 같이 생성할 수도 있다.
glm::mat4(1.0); // 생성자로 1.0 만 넘기기
glm::mat4 mat(1.0);

예상한 대로 결과가 나온다.
회전 행렬
glm::rotate() 함수를 사용한다.
변환할 4차원 행렬, radian 단위의 회전 각도, 회전축 벡터를 넣어주면 된다.
회전축을 임의로 지정할 수 있는 걸 보면 쿼터니언을 쓰는 것 같다.
라디안값은 glm::radians() 함수를 사용해서 degree 를 radian 으로 변환할 수 있다.

radians 함수에 degree 값을 넘길 땐 뒤에 f 를 붙여서 float 로 써야한다.
회전 축은 z축을 사용한다는 의미로 (0, 0, 1) 벡터를 입력했다.

기존 translate 행렬에 회전까지 적용하면 위와 같이 출력된다.
sin, cos 45도는 2분의 루트2 이므로, 대략 0.7의 값이 나왔다.
크기 변환 행렬
scale 변환은 scale() 함수를 사용한다.
변환할 4차원 행렬과, x, y, z 축 방향으로 몇 배씩 크기를 조절할지를 vec3 형태로 넘기면 된다.

스케일 변환은 헷갈리지 않도록, 기존 translate 행렬에 대해서 적용했다.
이렇게 기존 변환 행렬을 또 가져다가 사용할 수 있는 장점이 좌표계 변환 방식의 장점인 것 같다.

실행결과는 위와 같다.
복합 변환

위에서 본 것처럼 변환 행렬을 이어서 써주면된다.
기존 행렬을 재사용하지 않으려면 이렇게 덮어쓰듯 함수를 호출하면 된다.
아래는 전체 예제 코드이다.
#include <stdio.h>
#include <iostream>
#include <glm\glm.hpp>
#include <glm\gtc\matrix_transform.hpp>
#include <glm\gtc\type_ptr.hpp>
#define GLM_ENABLE_EXPERIMENTAL
#include <glm/gtx/string_cast.hpp>
void print_mat4(glm::mat4& mat);
int main() {
glm::mat4 mat;
// 원소 하나 초기화
mat[0][0] = 0;
mat[1][0] = 1;
mat[2][0] = 2;
// 열 벡터로 초기화
mat[3] = glm::vec4(3.0, 3.0, 3.0, 3.0);
// memcpy 함수 이용
float mat_val[16] = {
0, 0, 0, 0, // [0] 번째 행을 위에서부터 아래로 채운다.
1, 1, 1, 1,
2, 2, 2, 2,
3, 3, 3, 3
};
/**
* 실제로 만들어지는 행렬은 아래와 같다.
*
* 0 1 2 3
* 0 1 2 3
* 0 1 2 3
* 0 1 2 3
*
*/
memcpy(glm::value_ptr(mat), mat_val, sizeof(mat_val));
// print_mat4(mat);
//////////////////////////////////////////////////////
glm::mat4 origin;
float origin_mat_val[16] = {
1, 0, 0, 0, // [0] 번째 행을 위에서부터 아래로 채운다.
0, 1, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
};
std::cout << "origin\n";
memcpy(glm::value_ptr(origin), origin_mat_val, sizeof(origin_mat_val));
print_mat4(origin);
// 이동 행렬 적용
std::cout << "\norigin * T\n";
glm::mat4 translate = glm::translate(origin, glm::vec3(1, 2, 3));
print_mat4(translate);
// 회전 행렬 적용
std::cout << "\norigin * T * R\n";
glm::mat4 rotated = glm::rotate(translate, glm::radians(45.0f), glm::vec3(0, 0, 1));
print_mat4(rotated);
// 스케일 변환 적용
std::cout << "\norigin * T * S\n";
glm::mat4 scaled = glm::scale(translate, glm::vec3(2, 2, 2));
print_mat4(scaled);
}
void print_mat4(glm::mat4& mat) {
for (int row = 0; row < 4; row++) {
for (int col = 0; col < 4; col++) {
std::cout << mat[col][row] << ' ';
}
std::cout << '\n';
}
}셰이더와 함께 쓰기
이렇게 만든 변환 행렬은 결국 정점에 곱해지기 위해 존재한다.
따라서 행렬을 최종 활용하려면 셰이더로 행렬을 넘겨야 한다.

당연히 행렬은 uniform 변수로 넘긴다.
4차원 매트릭스 타입의 uniform 변수를 생성하고, 위와 같은 방식으로 만든 행렬의 포인터를 넘겨준다.
물론 저렇게 안하고


이런 방식으로 넘길 수도 있다.
넘어온 행렬은 결국 화면에 그릴 정점의 최종 위치를 결정하는데 사용되기 때문에 vertex shader에서 사용하면 된다.

위 그림과 같이 행렬에 정점의 좌표 (모델좌표) 를 동차좌표계 방식으로 바꾼 형태를 쓰면 된다.
다음 글에서는 실제 셰이더로 정점을 찍은 다음, 해당 정점을 행렬 변환을 이용해 위치를 옮기는 실습을 정리하겠다.
'CS > HCI 윈도우즈프로그래밍' 카테고리의 다른 글
| [OpenGL] 17. Transformation (5) - Projection & Perspective Normalization (0) | 2024.04.20 |
|---|---|
| [OpenGL] 16. Transformation (4) - 셰이더에 행렬 변환 적용하기 (1) | 2024.04.19 |
| [OpenGL] 14. Transformation (2) - 복합 변환 (0) | 2024.04.18 |
| [OpenGL] 13. Transformation (1) - 변환의 기본 개념 (0) | 2024.04.17 |
| [OpenGL] 12. Shader (8) - 여러 Texture 생성하기 (0) | 2024.04.14 |
