곱셈

초등학교때 배운 곱셈 방식을 이용하면 이렇게 곱셈을 한다.
컴퓨터에서도 같은 방식으로 곱셈한다.
위에 곱하는 1000 을 곱해지는 수 ( = 피승수, multiplicand ) 라고 하고
아래에 곱하는 1001을 곱하는 수 ( = 승수, multiplier ) 라고 한다.
곱셈은 그 특성상, n bit 수와 m bit 수를 곱했을 때, 최대 n + m bit 수가 나올 수 있다.

MIPS 의 경우, 32bit 수와 32bit 수를 곱해 최대 64 bit 수가 결과로 나올 수 있다.
이 수는 레지스터 하나에 저장할 수 없기 때문에 2개 레지스터를 사용하여 저장한다.

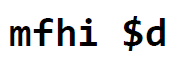

그래서 곱셈과 관련된 명령어는 위와 같이 사용한다.
mult 는 r, s 레지스터의 값을 곱한다. 결과는 hi, low 라는 별도 공간에 따로 저장된다.
결과물을 가져와서 레지스터에 저장할 때는 mfhi (move from hi) mflo (move from low) 명령어를 사용하여 직접 레지스터에 값을 옮긴다.
구체적인 이진수 곱셈 과정

위 이미지에서 곱셈하는 과정을 보면,
1000 과 1 을 곱하고
1000 과 0 을 곱하고
1000 과 0 을 곱하고
1000 과 1 을 곱하는데
결과물은 각각 한 칸씩 뒤로 밀리면서 더해진다.
결과물을 한칸씩 미는 것은 비트 시프트 연산과 같다.
따라서 아래와 같은 과정으로 계산을 할 수 있다.
1. 승수의 가장 오른쪽 bit 가 1이면 결과물에 피승수를 더한다.
2. 피승수를 왼쪽으로 1 시프트 한다. (자리수 증가), 승수는 오른쪽으로 1 시프트 한다.
3. 1, 2를 32번 반복한다. (승수의 bit 수 만큼 반복)
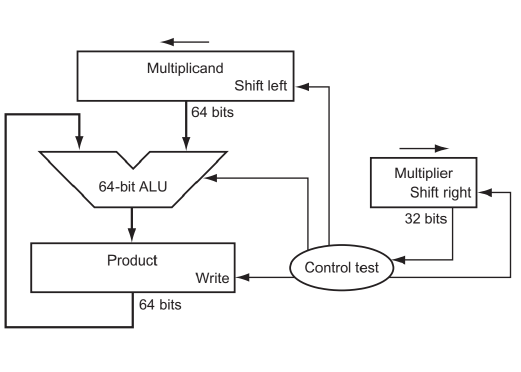
이를 회로도로 나타내면 위와 같다.
회로에서 제일 먼저 시작하는 곳은 'control test' 이다.
컨트롤 테스트는 제일 먼저 승수의 가장 오른쪽 비트를 관찰한다.
만약 이 값이 1이라면 현재 피승수를 product 에 더한다.
(위 이미지에서 product 에 대한 wrtie 는 write enable 신호를 준다는 뜻이고, 실제 결과는 ALU 에서 나온 출력값이 들어간다.)
덧셈이 끝나면 피승수를 왼쪽으로, 승수를 오른쪽으로 1칸 shift 한다.

플로우 차트로는 위와 같다.
부동 소수점
매우 작거나 매우 큰 정수가 아닌 실수를 표현하는 방식이다.
반대 개념으로 고정 소수점 방식이 있다.
고정 소수점 방식은 정수부와 실수부를 나눠서 따로 이진수로 저장하는 방식이다.
소수점의 위치가 고정되어 있어 '고정 소수점' 방식이라고 부른다.
이 방식은 표현 가능한 수의 범위가 부동 소수점보다 작다는 단점이 있다.
부동 소수점은 어떻게 소수를 표현하는지 살펴보자.

소수를 표현할 때, 과학적인 notation으로는 위와 같은 형식으로 표현한다.
정수부를 1자리로 고정하고, 나머지 소수부로 유효숫자를 결정한 뒤, 실제 자리수는 10의 거듭제곱꼴로 표현한다.
그리고 이렇게 과학적 notation 정의가 지켜진 형식을 '정규화된' 형식이라고 한다. (normalized)
부동 소수점 방식에서 정수부에는 1이상의 수가 들어와야 한다. 0이 들어오면 정규화가 필요한 대상이다.
이진수는 숫자가 0과 1로만 구성되어 있으므로 정수부가 반드시 1로 고정된다.
따라서 아래와 같은 형식으로 소수를 표현하 수 있다.

따라서 저 x 와 y 값만 결정하면 소수를 나타낼 수 있다.

위에서 x에 해당하는 부분이 Fraction, y에 해당하는 부분은 Exponent 라고 한다.
이와 같은 부동 소수점은 IEEE std 754-1985 에 정의되어있다.
그리고 크기에 따라 Single Precision, Double Precision 방식이 있다.
Single Precision은 32bit 데이터로 소수를 표현한다.
MSB 1bit는 부호를 나타내는 bit 이다.
이후 8 bit 는 Exponent 를 나타내는 bit 이다.
1 + Fraction 한 값을 significand 라고 한다.
fraction 값이 0이상 1 미만의 값이므로, significand 값은 1 이상 2 만의 값이 나온다.
Exponent 는 원래 순수하게 지수값을 의미해야하지만, 부동 소수점 방식에서는 음수 지수를 나타내기 위해 Bias를 사용한다.
Sigle precision 에서는 bias 값이 127 이고, double 에서는 1023 이다.
8bit exponent 값은 unsigned 기준 0부터 255 사이의 값을 가진다.
이때 0과 255는 특수한 의미를 가지기 때문에 1부터 254를 사용할 수 있다.
따라서 127을 빼면 -126부터 127 사이의 지수를 표현할 수 있다.
이를 종합하면 single precision 의 표현 범위를 알 수 있다.
제일 작은 값은 exponent 가 1 일 때의 실제 지수 -126, Fraction 이 0 일 때 Significand 1.0 으로
1.0 * 2 ^ -126 = 1.2 * 10 ^ -38 의 값을 표현할 수 있다.
제일 큰 값은 exponent 가 254 일 때의 실제 지수 127, Fraction 이 11111... 이라 Significand 가 1.11111 = 10진수로 2다.
2.0 * 2 ^ 127 = 3.4 * 10 ^ 38 의 값을 표현할 수 있다.
그렇다면 exponent 가 0과 255 일 때는 각각 어떤 의미를 가질까?

이 그림을 보면 된다.
만약 exponent 가 0 인데, fraction 도 0 이라면, 실수 0 을 의미한다.
만약 exponent 가 0 인데, fraciton 이 0이 아니라면, 매우 작은 수를 표현하는 subnormal 이 된다.
기존 floating point 가 1.0 + fraction 을 한 값에 지수를 곱했다면,
subnormal 은 0.0 + fraction 을 한 값에, 지수는 가장 작은 2^-126 을 곱한 값을 사용한다.
만약 exponent 가 255 인데, fraction 이 0이라면, 무한대를 의미한다.
만약 exponent 가 255 인데, fraction 이 0이 아니라면 실수 체계로 표현할 수 없는 수 (NaN) 를 의미한다.
Example
-0.75 를 이진수 부동 소수점 방식으로 표현해보자.
우선 음수이므로 sign 비트는 1
0.75 = 0.5 + 0.25 = 2^-1 + 2^-2
따라서 이진수로 나타내면 0.11 이 되고, 이를 normalize 하면 1.1 ^ 2 ^ -1
따라서 Fraction 은 10000..00, exponent 는 -1 + 127 = 126 으로 01111110
따라서 32bit 로 나타내면
1 01111110 100000...000
가 된다.
거꾸로 11000000101000000...00 을 십진수 소수로 바꿔보자.
우선 부호는 1 이므로 음수이다.
Exponent 는 10000001 로 129 를 나타낸다.
따라서 실제 exponent 는 129 - 127 = 2
Fraction 은 010000..00 이므로 significand는 1.01 과 같다.
이제 이를 조합하면 -1.01 * 2^2 = 101 = -5.0 (십진수) 이 된다.
부동 소수점 덧셈
IEEE 754 포맷으로 표현된 두 소수점을 더한다고 하자.
두 소수를 더할 땐 아래 과정을 거쳐야 한다.
1. 자릿수를 맞춘다. ( 지수를 맞춘다 )
2. significand 부분을 더한다.
3. 결과를 다시 normalize 한다. 또 overflow, underflow 를 체크한다.
4. 반올림하고, 필요하면 다시 정규화한다.

10진수에 대해서는 위와 같다.
사실 유효숫자 개념으로 접근하면 처음에 10.015가 나온 순간 이미 연산이 끝나야 한다고 생각해는데, 정규화하면서 유효 숫자가 훼손된 느낌이라 이상하다고 생각했다.

이진수에 소수에 대한 부동소수점 덧셈이다.
1.111 + 1.100 에 대한 덧셈시, overflow, round 에 대해 처리하는 방식이 궁금해졌다.
내일 질문하고 들은 답변을 토대로 다시 정리해봐야겠다.
1. 위 덧셈은 32bit 체계에서 1.111, 1.100 을 표현한 것을 가정했는가 아니면 3bit fraction 으로 표현한 것을 가정한건가
→ 위 덧셈은 fraction 이 3bit 인 것으로 가정했다.
2. 부동 소수점 체계를 사용할 때는 정수부가 1 일 때를 가정하고 연산하는데, 위처럼 10.011 인 상태가 중간에 표현가능한가
→ 별도 하드웨어에 캐리를 저장하는 방식으로 구현할 수 있다.
3. 10.011 로 연산한 상태에서 right shift 해서 노말라이즈를 하면 LSB 가 버려지면서 1.001 이 되는 것 아닌가?
이 경우, round 는 할 필요가 없지 않은가?
→ 버리는 방식의 round도 있긴 한데, 다른 방식으로 round 한다면 별도 하드웨어에 버려지는 LSB를 모아서 저장해두고, 이 값을 이용해서 round 할 수 있다.
4. 십진수에서 round 하는 방식은 이해가 되는데, 이진수는 잘 이해가 안된다. 어떻게 이진수의 round를 하는가?
→ 이진수의 round 방법은 방식이 다양하다. 그래서 파이썬의 round 와 엑셀의 round 방식도 실제로 다르다.
시험에서는 round 할 일이 있을 경우, 어떻게 하라고 지정해줄 것이다.
Overflow & Underflow
부동 소수점에서의 오버플로우 / 언더플로우는 지수와 관련이 있다.
결국 정수부가 아무리 커져도 normalize 한 뒤 이를 지수에 반영하면 되기 때문에, 정수부 자릿수가 1을 넘어가는 것은 상관없다.
Single Precision Floating Point 에서의 Overflow 는 양의 지수로 표현가능한 2^127 를 넘어가는 지수를 가질 때 오버플로우가 발생한다.
반면 같은 기준의 Underflow 는 음의 지수로 표현가능한 2^-126 을 넘어가는 더 작은 지수를 가질 때 언더플로우가 발생한다.

참고로 실수 덧셈하는 유닛을 FP Adder 라고 한다.
이 하드웨어의 구조는 위와 같다.
단계가 여러개로 나눠져 있는 만큼, 덧셈보다 더 많은 사이클을 필요로 해서 파이프라이닝을 적용하기도 한다.
'CS > 컴퓨터 구조' 카테고리의 다른 글
| [컴퓨터 구조] 11. Single Cycle MIPS - Fetch (0) | 2024.04.19 |
|---|---|
| [컴퓨터 구조] 10. Single Cycle MIPS - 개요 (0) | 2024.04.18 |
| [컴퓨터 구조] 8. Computer Performance (0) | 2024.04.16 |
| [컴퓨터 구조] 7. MIPS 명령어 총 정리 (0) | 2024.04.16 |
| [컴퓨터 구조] 6. MIPS Branch Instructions (0) | 2024.04.15 |
