Language
우리가 사용하는 자연어나 프로그래밍 언어에는 공통점이 있지만, 이를 명확하게 규정하는 것이 쉽지 않다.
따라서 우리가 사용하는 언어를 더 쉽고 엄밀하게 다루기 위해서, 언어를 수학을 통해 추상화 해보려고 한다.
그리고 이렇게 추상화된 언어를 Formal Language 라고 한다.
alphabet
알파벳 ∑ = symbols 로 구성된 공집합이 아닌 유한집합
∑ = {a, b} => 이 알파벳을 사용하여 만드는 언어는 a, b 로만 구성될 수 있다.
∑ = {0, 1} => 이 알파벳을 사용하여 만드는 언어는 0, 1 로만 구성될 수 있다.
String
유한한 길이를 갖는 symbols의 나열 (무한히 나열한 것은 아니다.)
위 예시에서의 알파벳을 사용하여 문자열을 구성한다면 다음과 같은 문자열을 만들 수 있다.
u = abaaa
v = 011010
문자열과 관련된 연산, 성질에 대해서는 다음과 같이 정의한다.
w = a1a2a3...
v = b1b2b3...
과 같은 알파벳의 나열일 때,
concatenation : 두 문자열을 이어붙인다.
wv = a1a2a3....b1b2b3...
reverse : 문자열을 뒤집는다.

length : 문자열의 길이. 문자열이 갖는 심볼의 개수를 말한다.
|w| 와 같은 형태로 사용한다.
이때 심볼 하나의 길이 |a| = 1 이며, 기존 문자열에 심볼을 하나 추가하면 |wa| = |w| + 1 이다.
empty string : 비어있는 문자열은 람다 기호를 사용하여 나타낸다.

substring: 문자열 w 내에 존재하는 '연속된 심볼' 문자열을 말한다.
prefix : 어떤 문자열에서 맨 앞에서부터의 연속된 부분 문자열
suffix : 어떤 문자열에서 맨 뒤에서부터의 연속된 부분 문자열

Language
심볼, 알파벳, 문자열로부터 언어 (language) 에 대한 정의를 내릴 수 있다.

어떤 문자열 w에 대해서, 이 문자열을 n 번 concatenate 한 문자열을 위와 같이 거듭제곱 형태라 작성할 수 있다.
이때 이 문자열을 0 번 concatenate 한다고 하면, 빈 문자열을 나타내게 된다.
(이 표현은 매우 자주 나오므로 익숙해지자.)

알파벳을 표현할 때는 시그마 기호를 이용하여 나타낸다.
이때 시그마 기호 위에 * 첨자를 붙이면, 주어진 알파벳을 0번 이상 사용하여 만들 수 있는 모든 문자열을 나타낸다.
이렇게 * 첨자를 붙인 것을 star closure 라고 부른다.
만약 * 대신 + 를 붙이게 되면, 주어진 알파벳을 1번 이상 사용하여 만들 수 있는 모든 문자열을 의미한다.
이 기호는 positive clousure 라고 부른다.
두 기호로 나타내는 문자열들의 집합은 모두 무한집합이다.
이때 언어(Language) L 은 어떤 알파벳의 star closure 에 대한 부분집합을 말한다.
즉, 어떤 알파벳으로 만들 수 있는 모든 문자열의 집합 중 부분 집합을 말한다.
(어떻게 보면 당연하다)
그리고 언어 L 의 문장(sentence)은 L 에 속해있는 문자열을 말한다.

예를 들어, 어떤 언어의 알파벳이 {a, b} 로 구성되어 있다고 해보자.
L1 이라는 언어는 a, aa, aab 라는 3개의 문자열로 구성된 유한 집합이다.
그리고 특별하게 이 문자열들을 L1 의 sentence 라고 부른다.
L1은 이 알파벳 집합의 스타 클로저의 부분집합이므로 충분히 언어가 될 수 있다.
L2는 a와 b를 모두 동일하게 n번 concatenate 한 문자열로 구성된 무한 집합이다.
(심볼 하나도 문자열이며, 이 문자열에 n 승을 취하면 그 문자열을 n번 concatenate 한 것이다.)
이 언어에 속하는 문자열은 빈 문자열, ab, aabb, aaabbb, 와 같은 문자열들이 있을 것이다.
이렇게 언어를 정의하는 집합은 보통 무한집합의 형태로 표현하는 경우가 많다.
formal language 에서 언어는 결국 '문장의 집합'이다.
그렇다면 이 언어에 대해서도 집합과 비슷한 연산들이 수행할 수 있을 것이다.
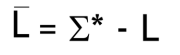
어떤 언어에 대한 여집합은 이렇게 알파벳의 star closure 에서 언어 집합을 뺀 나머지이다.
L의 정의가 알파벳의 star closure의 부분집합이므로 자명하다.

어떤 언어의 reverse 는 그 언어를 구성하는 모든 문장에 대한 reverse 와 같다.

두 언어 L1, L2 에 대한 concatenation은 각 언어의 문장을 concatenate한 문장의 집합이다.
그러면 무수히 많은 문장 조합이 가능할 것이다.
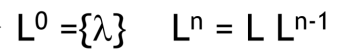
이때 자기 자신을 concatenate 하는 경우에 대해 L의 거듭제곱 형태로 아래와 같이 표현할 수 있다.
L의 0승은 L에서 어떤 문장도 가져오지 않고 '덧붙인 것' 이므로 공집합이 아니라 빈 문자열로 구성된 집합이 나온다.
덧붙이는 시작점은 빈 문자열이고, 빈 문자열에 대해 각 언어에서 문장을 꺼내 조합하여 붙이는 것과 같다고 생각하면 된다.
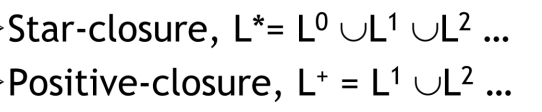
그리고 각 concatenate 조합을 합하여 언어에 대해서도 star closure, positive closure를 만들 수 있다.
연습 문제
L = { a^n b^n : n >= 0 } 이라고 해보자.
L^2 은 어떻게 쓸 수 있을까?
L^2 = 각각의 L에서 꺼낸 문장들의 concatenate 집합이므로, { a^n b^n a^m b^m : n >= 0, m >= 0 } 으로 나타낼 수 있다.
L^R 은 어떻게 쓸 수 있을까?
L^R 을 집합으로 표현한다면, L을 구성하는 모든 문장을 뒤집으면 되므로, { b^n a^n : n >= 0 } 으로 표현할 수 있다.
Grammar
formal language 의 문법 이전에 우리가 사용하는 언어의 문법을 먼저 생각해보자.
영어라는 언어 역시 다양한 문장들의 집합으로 나타낼 수 있다.
하지만 규칙이 너무 다양하고 복잡하기 때문에 set notation으로 표현하기란 쉽지 않다.
그래서 이 언어를 표현하는 방법으로 '문법' 이라는 방법이 등장했다.
예를 들면 영어의 문법 일부를 아래와 같이 나타낼 수 있다.

문장은 명사절과 동사절의 concatenate 이라고 정의하고,
명사절은 관사와 형용사와 명사의 조합, 동사절은 동사와 형용사의 조합이라고 정의한다.
관사는 A, The 라는 문자열 중 하나가 되고, 형용사, 명사, 동사, 부사도 각각이 변환될 수 있는 문자열이 있다.
이렇게 위와 같은 표현으로 정말 다양한 영어 문장들을 표현할 수 있게 되며,
그 문장들을 원소로 하는 영어 언어를 표현할 수 있게 된다.
이제 수학적으로 문법을 표현해보자.
문법은 언어를 나타내는 규칙, 메커니즘이라고 생각할 수 있으며, 다음 4가지 요소로 구성된다.

V 는 문법을 정의하는데 사용한 변수의 유한집합
T 는 각 변수가 최종적으로 변화될 터미널들의 유한집합
S 는 시작 변수
P 는 각 변수가 다른 변수/터미널로 어떻게 변화할 수 있는지를 나타낸 규칙(프로덕션)들의 집합
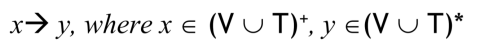
이때 프로덕션은 위와 같이 화살표로 나타낸다. x -> y 라고 하면, x는 y를 produce 한다고 말한다.
이때 x 는 비어있지 않은 V, T 의 합집합에 속하고, y는 변수와 터미널의 합집합의 star closure 이다.
또한 V, T 는 서로 겹치지 않는 서로소 집합인 동시에, 두 집합 모두 공집합이 아닌 집합이다.
위에서 본 영어 문법으로 본다면
sentence (위에서 다룬 sentence와 이름만 같다. 여기서는 변수 이름으로 사용된 것이다.)
noun-phrase 와 같이 검은 글씨로 작성된 부분이 모두 '변수' 이다.
T는 파란 글씨로 작성된 문자열들이 터미널이다.
S는 시작 변수로, sentence 라는 변수가 해당한다.
이 변수로부터 시작해야만 언어를 구성하는 온전한 하나의 문장이 만들어지기 때문이다.
P는 화살표로 표기된 모든 생산 규칙(프로덕션) 집합을 말한다.

이 외에도 w 가 z를 유도한다 (derives) 라고 하면 위와 같은 기호로 나타낼 수 있다.
이때 유도한다는 것은 실제 문장이거나, 문장으로 마무리 될 수 있는 sentential form 을 말한다.
만약 w 가 uxv 의 형태이고, z 가 uyv 의 형태일 때, x → y 라는 프로덕션을 이용하면 uxv 가 uyv 형태로 바뀔 수 있으므로 이 전체적인 sentential form 의 변환을 유도라고 하는 것이다.

'문장' 은 '언어' 라는 집합의 원소로서, 위 영어 문법 기준으로는 'The large dog runs fast' 와 같이 터미널로만 구성된 것을 말한다. 하지만 변수로부터 확장하는 과정에서 파란색(터미널)과 검은색(변수)이 섞여있는 부분은 '문장' 이라고는 할 수 없다. 하지만 프로덕션 (규칙) 을 적용하면 잠재적으로 문장이 될 수 있는 형태이기 때문에 sentential form 이라고 부른다.
start variable 도 sentential form 이다.
다시 '유도' 로 돌아온다면, 만약 어떤 것이 다른 것을 유도(derives)한다면, 이는 sentential form 이 다른 sentential form 또는 sentence를 유도한다는 것을 말한다.
(프로듀스는 '규칙' 에 대해서만 말하는 것이다. 유도는 규칙을 실제로 적용하는 과정에서 사용하는 것으로 이해했다.)
예를 들면, article 은 The 라는 터미널을 produce 하지만, article 자체는 문장이 될 수 없으므로 sentential form 이 될 수 없다. 따라서 이때는 '유도한다' 라는 말을 쓸 수 없다.
다른 변수나 터미널을 produce하는, 주어진 프로덕션들을 잘 활용해서 sentential form 을 다른 sentential form 이나 문장으로 바꾸는 과정을 'derivation' 이라고 하는 것이다.

정리하면 sentential form 또는 sentence 인 w 에 대해 위와 같이 나타낼 수 있다.
먼저 S 라는 시작 변수에서부터 w1, ...., wn 을 거쳐 w라는 sentential form 또는 sentence를 유도한다.
이때 이 중간 과정을 생략하고 '1개 이상의 여러 단계를 거쳐서 유도했다' 라는 것을 말할 때 * 첨자를 사용하여 밑의 표현처럼 쓸 수 있다.
마지막으로 언어와 문법 사이의 관계를 다시 생각해보자.
언어는 심볼의 집합인 알파벳들의 star closure로 나타낸 집합의 부분 집합으로,
이 알파벳으로 만들 수 있는 정해진 문자열 (문장) 의 집합을 말한다.
이때 이 문장들의 집합을 일반적인 집합 notation으로 표현하기 힘든 경우도 많기 때문에 '문법' 의 형태로 언어를 표현할 수 있다.
만약 어떤 문법 G = (V, T, S, P) 가 어떤 언어 L 을 생성한다면 (generate) 그 언어는 다음과 같이 표현한다.

집합 기호를 보면, 각 문장들은 터미널 집합의 star closure, 즉 각각의 터미널들의 조합(concatenate)으로 문장이 만들어지는데, 이 문장들은 반드시 S 라는 시작 변수로부터 시작해서 임의 횟수의 derivation을 거쳐 만들어지고, 이 문장들의 집합이 바로 L 이라는 의미이다.
연습 문제

이 문법으로부터 만들어지는 L 을 집합으로 표현해보자.
먼저 문법에서 사용된 모든 변수는 S 하나밖에 없다. (그러면 당연히 시작변수 역시 S 일 것이다.)
문장을 구성하는데 사용되는 터미널은 a, b 2개이며, production 은 S → aSb | 람다 라는 규칙이 있다.
시작변수는 aSb 라는 sentential form 또는 람다라는 sentence를 produce 하는 것이다.
(즉, 2개의 production 이라고 말할 수 있다.)
정답은 간단하다 L = {a^n b^n : n >= 0 } 을 문법으로 표현한 것이다.
이 언어의 문장은 빈문자열, ab, aabb, aaabbb 와 같은 문장이 있을 것이다.
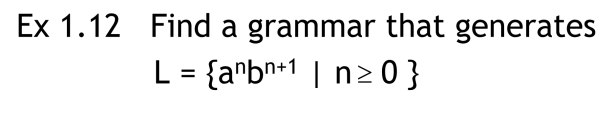
이번엔 거꾸로 언어에 대한 집합 표현이 주어졌을 때, 이를 문법(grammar) 표현으로 바꾸어보자.
이전 예제에서 b가 항상 a보다 1개 더 많은 상황이므로 다음과 같이 나타낼 수 있다.
G = (V, T, S, P)
G = ( {S}, {a, b}, S, { S → aSb | b } )
위의 정의에서 S가 produce 하는 부분을 aSb 또는 b로 정의하면 위 언어를 구성하는 문장을 만들 수 있다.
교수님과 수업을 들을 당시 나의 풀이는 다음과 같았다.
G = ( {S, V}, {a, b}, S, { S → Vb, V → aVb | λ } )
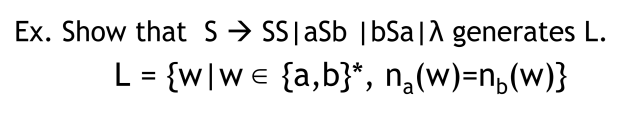
이번 문제는 그림과 같은 문법을 통해 만들어지는 언어에 대해, 이 언어를 집합으로 표현하면 위와 같은 형태가 되는 것을 증명하는 것이다.
이때 문법은 G = (V, T, S, P) 형태에서 P 만 적은 형태로 간단하게 나타내었다.
지금 그림에서 보는 P 는 총 4개의 productions 로 이루어진 집합이다.
이때 production 중에 SS 가 있는 이유는 abba 와 같은 문장을 생각해보면 알 수 있다.
만약 SS 가 없다면 양 끝이 같은 문자열을 만들 수 없을 것이다.
언어 L의 집합 표현식을 보면, 이 언어는 w 라는 문장으로 구성된 집합이다.
이때 w 는 {a, b} 의 star closure 이므로 알파벳으로 a, b 로 만들 수 있는 모든 문자열에 속하는 것이 첫번째 조건이고,
두번째 조건은 이 문자열의 a, b 의 개수가 동일하다는 것을 의미한다. (n_a(w) = w 안의 a의 개수를 말한다.)
이제 이를 귀납법으로 한명 증명해보자.
우선, 첫번째 문법을 통해서 표현되는 언어의 집합을 L(G) 라고 하자.
그러면 우리는 L(G) = L 임을 증명하면 된다.
이때 두 집합이 같다는 것을 보일 때는 두 집합이 서로의 부분집합으로 들어간다는 것을 보이면 된다.
먼저 L(G) ⊆ L 을 보이는 것은 저 문법을 통해 유도되는 문장은 a, b 의 개수가 같을 수 밖에 없음을 보이면 된다.
다음으로 L ⊆ L(G) 를 보이는 것은 L 에 존재하는 임의의 문장을 꺼냈을 때, 이 문장을 G 라는 문법을 통해서 유도할 수 있음을 보이면 된다.
1. L(G) ⊆ L
만약 주어진 문법을 통해서 a를 하나 만들고 싶다고 해보자.
그러면 주어진 production 중에서 어떤 것을 사용해도 a를 추가하려면 aSb, bSa 를 사용해서 만들어야 하므로 b가 반드시 생기게 된다.
반대로. b 에대해서도 b를 하나 만들고 싶다고 하면 반드시. a 도 하나 추가할 수 밖에 없다.
따라서 이 문법을 통해 유도된 문장은 언제나 같은 개수의 a, b를 가지므로 L의 원소이기도 하다.
2. L ⊆ L(G)
이 부분은 한번 직접 귀납법을 사용해서 증명해보자.
우선 a, b 의 개수가 같다는 것은 문자열의 길이가 짝수라는 것을 의미한다.
여기에서 착안해서 문자열의 길이가 2 x 1 일때 성립함을 보이고, 만약 2 x i 에 대해 i = 2 .. N 까지 성립한다고 가정할 때 N+1도 성립한다는 것을 증명하면 귀납법을 통해 증명할 수 있다.
- basis
먼저 주어진 문법 G로 L에 속하는 길이가 2x1 이하인 문장을 만들 수 있다.
L 안에는 길이가 2 이하인 문장이 3개 있으며, 문법 G를 사용하여 다음과 같이 3개의 문장을 각각 유도할 수 있다.

- assumption
G를 사용하면 L 내에 있는 길이가 2 x i 인 문장을 만들 수 있다고 가정해보자.
- reduction
그러면 L 내에 있는 길이가 2 x (i+1) 인 문장을 만들 수 있음을 증명해보자.
먼저 2i + 2 길이를 갖는 문장을 다음과 같이 4가지로 분류해볼 수 있다.
1. a ... b
2. a ... a
3. b ... a
4. b ... b
그리고 이 4가지를 i 까지 모두 주어진 문법을 통해 만들 수 있다고 가정할 때 추가적으로 만들 수 있음을 보이면 된다.
먼저 1, 3 번은 매우 쉽다.
i 까지 주어진 문법을 통해 만들었다면 그 다음에는 또 다시 주어진 문법의 production 중 aSb, bSa 를 사용하면 만들 수 있기 때문이다.
어려운 부분은 2, 4 번을 증명하는 것인데, 먼저 간단하게 길이가 6인 경우를 생각해보도록 하자.
만약 길이가 6이라면 a, b 의 개수가 모두 3개로 동일할 것이다.
이때 한번 다음과 같은 변수를 만든다고 해보자.
이 변수의 초기값은 0이며 a를 만나면 +1, b를 만나면 -1 이 된다.
이제 길이가 6인 문자열을 구성하는 심볼을 하나씩 훑으면서 이 변수 값의 변화를 따라가보자.
만약 abbaab 라는 문장을 읽는다면 0 -> 1 -> 0 -> -1 -> 0 -> 1 -> 0 과 같은 형태로 변화할 것이다.
L에 속해있는 어떤 문장에 대해 이 변수값의 변화를 따진다면 이 변수값은 0에서 시작해서 최종적으로는 0으로 돌아올 것이다.
이때 이번엔 증명하고자 하는 2번 문장을 생각해보자.
2번 문장은 a 에서 시작해서 a로 끝나므로, 이 변수값의 변화는 반드시 0 -> 1 -> .... -> -1 -> 0 의 형태가 되어야 한다.
이 변수 값의 변화를 그래프로 나타내보면 아래와 같이 나타낼 수 있다.

이때 이 값의 변화는 반드시 연속적이라서, +1 에서 시작한 값이 -1을 찍었다가 0으로 돌아오려면 그 중간에 반드시 적어도 1번은 0을 찍어야만 한다.
그 시점을 위 그림과 같이 점선으로 표현했을 때, 이 점선을 기준으로 왼쪽도 0 ... 0 이 되는 지점이 있고, 오른쪽도 0...0 이 되는 지점이 있다.
즉, a에서 시작해서 a로 끝나는 문장은 반드시 S -> SS 라는 production을 사용하여 나타낼 수 있다.
이때 이 프로덕션을 사용하여 생산한 각 S 는 반드시 길이가 2i 보다는 짧기 때문에, 우리가 한 가정에 의해 G를 이용하여 L에 속하는 문장으로 만들어낼 수 있다.
S -> SS 역시 G를 구성하는 문법이므로 최종적으로 G를 이용하면 a ... a 형태의 2 x i 길이의 문장을 만들 수 있음을 보이게 되었다.
b ... b 역시 같은 이치로 성립하므로 우리는 귀납법을 통해 주어진 문법이 주어진 언어를 나타낼 수 있음을 증명하였다.
'CS > 오토마타' 카테고리의 다른 글
| [오토마타] 6. FA 에서 state 개수 줄이기 (0) | 2024.10.22 |
|---|---|
| [오토마타] 5. NFA (Nondeterministic Finite Accepter) (0) | 2024.10.20 |
| [오토마타] 4. DFA (Deterministic Finite Accepter) (0) | 2024.10.17 |
| [오토마타] 3. 오토마톤 (0) | 2024.10.17 |
| [오토마타] 1. 기본적인 수학적인 지식 (1) | 2024.10.12 |
