NFA
Nondeterministic Finite Accepter
DFA와 마찬가지로 유한한 저장공간을 가지며, 답을 yes / no 로만 내는 기계를 말한다.
다만 Nondeterministic 이므로, 현재 상태에서 특정 인풋이 주어졌을 때, 다른 상태로 넘어갈 수 있는 길이 여러개가 있거나 없을 수 있는 기계를 말한다.
구성요소 자체는 DFA와 동일하므로 DFA와 유사하게 정의된다.


이때 𝜹 에 들어갈 수 있는 transition function는 DFA와 다르다.
델타에는 DFA와 마찬가지로 𝜹(Qx, a) = Qy 로 표기할 수 있다.
다만 이때 Qy가 하나의 상태가 아니라 여러 개의 상태 집합일 수 있으며, 입력 심볼에도 빈 문자열 람다가 들어올 수 있다.
위 정의에서 말하는 2^Q 는 power set을 말하며, 어떤 집합이 가질 수 있는 모든 부분집합의 집합을 말한다.
{1, 2} 라는 집합의 파워셋은 {φ, {1}, {2}, {1, 2}} 이렇게 4개의 집합을 원소로 갖는다.
즉, NFA의 공역에는 모든 종류의 상태집합이 아무거나, 공집합도 포함해서 들어올 수 있는 것이다.
DFA보다는 조금 더 제약이 없는 형태이지만, 어쨌든 결국 NFA도 엑셉터로써 어떤 문자열이 주어졌을 때 이 문자열이 문장인지 아닌지 판별만 해주면 된다.
NFA에서 주어진 문자열이 문장인지 판별할 때는 해당 문자열의 입력으로부터 final state 로 갈 수 있는 walk가 존재하는지 여부로 판별한다.
DFA에서는 하나의 문자열 입력에 대해서는 하나의 walk 만 존재했지만, NFA 에서는 walk가 여러개 있을 수도 있고 없을 수도 있다.
하지만 몇 개의 walk 든 간에, 1개라도 final state로 갈 수 있다면 해당 문자열은 문장이 된다.

예를 들어 위와 같은 트랜지션 그래프를 보자.
위 그래프는 q0 에서 a 라는 심볼을 읽었을 때 갈 수 있는 상태가 2가지가 있다.
따라서 결정적이지 않으므로 NFA 이다.
이 NFA는 aa 라는 문자열이 주어지면 이 문자열을 문장으로 판단한다.
q0 → q4 → q5 라는 walk를 따라가면 final state에 존재하기 때문이다.
q0 → q1 → q2 라는 walk를 따라가면 non-final state 에 존재하긴 하지만, final state로 갈 수 있는 walk가 적어도 1개 존재하므로 문장으로 받아들여질 수 있다.

이 그래프도 NFA의 트랜지션 그래프를 나타낸다.
모든 각각의 상태에 대해 0, 1 에 대한 트랜지션이 존재하지 않으며, 람다라는 트랜지션도 존재하기 때문이다.
이 기계는 01 은 문장이 될 수 없지만, 10은 문장이 될 수 있다.
빈 문자열은 꼭 트랜지션을 타지 않고 q0에 머물러도 괜찮으므로 역시 문장이다.

NFA 역시 extended transition function 을 가질 수 있다.
만약 𝜹(qi, w) = { qj, ... } 로 표현할 수 있는 트랜지션 함수가 있다면 qi → qj 로 가는 walk 가 존재하며, 그 반대도 마찬가지이다.
DFA 와 다르게, 함수의 결과가 집합으로 표현만 되었으며, 이 명제는 어떻게보면 당연하다.

이 그래프를 봤을 때 다음 트랜지션 함수는 올바른 트랜지션 함수일까?

q1 상태에서 몇 번의 함수를 적용하든 갈 수 있는 상태들을 나열해보면 q0, q1, q2 모두 갈 수 있다.
(이 그래프는 사이클을 이루고 있으니 다른 상태에 대해서도 트랜지션 함수를 여러번 적용한다면 어느 상태로든 갈 수 있다.)

NFA 역시 그 NFA가 문장으로 판별하는 문자열들을 대상으로 '언어' 를 표현할 수 있다.

한번 이 NFA가 만들어내는 문장을 생각해보면
빈 문자열
10
1010
101010
....
으로 표현할 수 있다.
따라서 L = { (10)ⁿ : n >= 0 } 이라고 표현할 수 있다.
만약 누군가 q2 상태에서 0을 입력받으면 어디로가는가? 라고 묻는다면 트랜지션 함수는 𝜹(q2, 0) → φ 이므로, 정의되어있지 않다고 말할 수 있다. 이를 undefined 또는 deconfiguration 라고 말하기도 한다.
NFA 와 DFA
그런데 NFA는 뭔가 더 복잡하기만 한 것 같은데 Nondeterministic 한 기계가 왜 필요한지 의문이 들 수 있다.
나중에 결론을 내리겠지만, 모든 NFA는 사실 DFA로 바꿔서 표현할 수 있다.
하지만 그럼에도 불구하고 NFA가 유용한 상황도 있다.

다음과 같은 예시를 보자.
언어 역시 결국은 문장들의 집합이므로 두 개 집합의 합집합으로도 표현할 수 있다.
이 예시를 나타낼 때 DFA, NFA 어떤 것이 더 편할까?
이 언어가 갖는 문장은 a의 개수가 3개이거나, 짝수 개이다.
이 문장은 DFA, NFA 모두 다 표현이 가능하지만, 간단하게 생각하면 NFA로 표현하는 것이 더 편하다.

NFA로는 위 그림과 같이 간단하게 표현할 수 있다.
Equivalent
두 Finite Accepter M1, M2 에 대해서, (DFA, NFA는 상관이 없다)
만약 L(M1) = L(M2) 로 두 기계가 만들어내는 언어가 동일하다면 두 기계는 equivalent 하다고 말할 수 있다.

예를 들어, 이 NFA 와 동일한 DFA를 그린다면, 빈 문자열, 01, 0101, 010101, ... 을 표현하는 DFA를 그리면 되므로 아래와 같이 그릴 수 있다.

그리고 이 기계가 만들어 내는 언어는 위 NFA 기계가 만드는 언어와 동일하므로, 두 기계는 서로 equivalent 하다.
equivalent 라는 성질에 대해서 한 가지 정리가 성립한다.
위에서 잠깐 적었던 정리로, 모든 NFA 는 equivalent 한 DFA로 변환할 수 있다는 것이다.
(수학적으로는 모든 NFA에 대해, 각 NFA는 그와 equivalent 한 DFA가 존재한다고 표현한다.)
이때 NFA를 DFA로 변환하는 방법은 다음과 같다.
1. NFA의 init state = q0 일 때, equivalent 한 DFA 의 init state 를 {q0} 라고 하자.
(집합 기호처럼 표현이 되어있는데, 그냥 이름을 중괄호를 껴서 지은 이름이라고 생각하자)
2. 다음 과정을 DFA의 속성 (각 state는 모든 종류의 symbol에 대해 outgoing edge를 가져야 한다)을 만족할 때까지 반복한다.
2-1. DFA를 구성하는 모든 종류의 state 에 대해, 각 상태마다 extended trasition function 즉, 𝜹*(state, symbol) 을 NFA를 보고 구한다.
2-2. 그 결과 어떤 {qi, qj, qk, ...} 라는 이름의 state에서 a라는 심볼을 받았을 때 {qi', qj', ...} 이라는 state로 갈 수 있다고 할 때, 이 state가 아직 DFA에서 정의되지 않았다면 이 state 를 추가한 뒤, 간선을 연결하고 a를 라벨링한다.
3. NFA의 final state를 참고하여, DFA의 final state를 적절하게 표시한다.
4. 만약 λ가 NFA에서 문장이었다면 DFA에서도 init state를 final state로 만든다.
예시를 살펴보자.

주어진 그래프는 NFA 그래프이다. 이 그래프를 DFA로 고쳐보자.
1. NFA의 init state를 기반으로 DFA의 init state를 { } 기호로 표시한다.

2. DFA가 되기 위해서는, 이 state로부터 나가는 모든 심볼에 대한 outgoing 간선이 있어야 한다.
outgoing 간선을 찾기 위해 NFA를 참고해보면,
q0 에서 0을 만났을 때는 q1 으로 가거나 자기 자신에게 되돌아 올 수 있고,
q0에서 1을 만났을 때는 반드시 q1로 간다.

이를 그래프로 나타내면 위와 같이 나타낼 수 있다.
위에서 저런 집합 기호로 표기한 상태를 만들었다는 것은, 그런 종류의 새로운 상태를 정의하겠다는 것과 같다.
(state 의 이름을 집합 기호로 표시했다고 봐도 좋다.)
이제 새로 추가된 state에 대해서 반복하자.
각 state에 대해서 0, 1 로 나가는 간선이 있어야 DFA가 될 수 있다.
{q0, q1} 이라는 종류의 state 에서 0을 입력받았을 때 가능한 경우의 수를 NFA를 보고 찾으면,
(q0 에서 0을 입력받았을 때 결과) + (q1 에서 0을 입력받았을 때 결과) 와 같다.
q0에서 0을 받으면 q0 또는 q1
q1에서 0을 받으면 q2로 가므로
{q0, q1} 에서 0을 받으면 {q0, q1, q2} 로 가게 된다.
이런 종류의 state는 없으므로 새로 추가하고, outgoing 간선에 0을 라벨링한다.
그러면 아래와 같이 만들어진다.

{q0, q1} 에 대해서 1이 입력으로 들어오면 {q1, q2} 가 될 수 있다.
이 과정을 DFA가 만들어질 때까지 반복하면
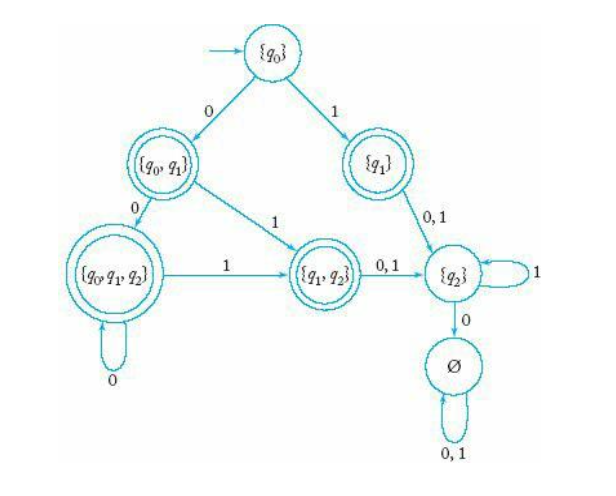
이런 그림이 만들어진다.
이 그림에서는 3번 과정인 final state 표현까지 적절히 된 상태이다.
q1이 final 이므로 q1을 포함하는 집합 표현을 가진 state들을 모두 final state 로 만들면 된다.
4번 과정으로 λ를 받을 수 있다면 init state도 final state로 만들어주면 끝이다!
또 다른 예시도 살펴보자.

이 NFA 와 equivalent 한 DFA를 만들어보자.
DFA를 만들 때는 각 상태를 NFA의 상태를 이용해서 정의한다고 생각하면 좋다.
초기 상태는 DFA, NFA가 모두 동일하므로 {q0} 로, NFA의 q0 상태를 유일한 원소로 갖는 집합을 상태로 정의한다.

이제 이 state에 대해 a, b 를 고려해주자.
먼저 NFA에서 q0일 때 a라는 입력을 받으면 갈 수 있는 상태는 q1 과, λ를 추가적으로 거쳐서 간다면 q2도 갈 수 있다.
(λ는 DFA에서 고려하지 않으므로, NFA에서 갈 수 있는 상태를 따질 때는 이동 횟수에 상관없이(𝜹*) a라는 입력을 한번만 쓴 것과 동일한 효과로 갈 수 있는 모든 상태를 생각하면 된다.)
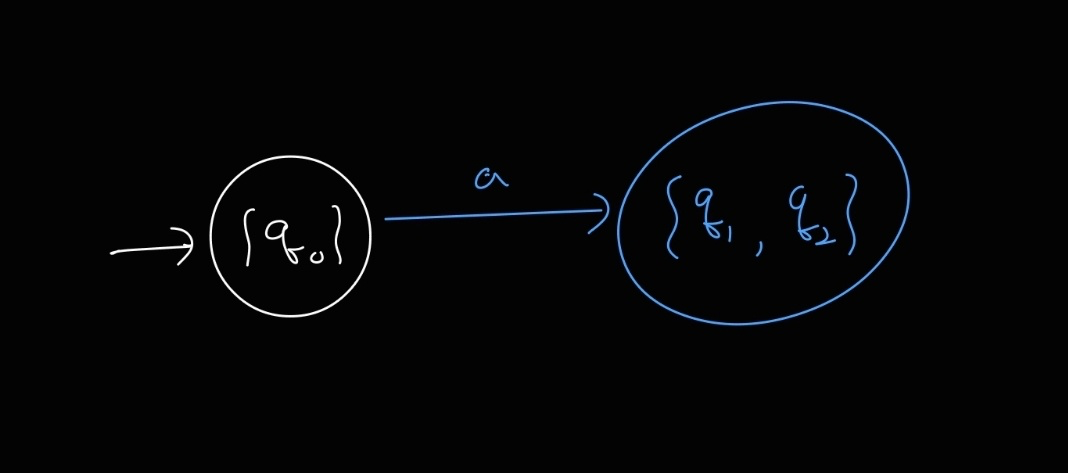
이번엔 q0 상태에서 b 라는 입력을 받을 때 갈 수 있는 모든 경우를 고려해보자.
NFA 그래프를 보면 갈 수 있는 상태가 없다. (정의되어 있지 않다.)
하지만 DFA 에서는 상태로 만들어야 하므로, 이런 상태를 공집합 기호로 나타내서 만든다.
(NFA에서 트랜지션 함수는 상태 집합의 파워셋, 따라서 공집합 기호를 가질 수 있다는 것을 생각하면 자연스럽다.)

간단하게 공집합만 생각해보면, 공집합은 NFA 에서 정의되어 있지 않으므로, 공집합 state에서 a, b로 나가는 간선은 그대로 공집합으로 돌아온다. (따라서 공집합 state는 trap state 라고 생각하면 된다.)

이번엔 {q1, q2} 상태에 대해서 입력이 a가 들어올 때를 생각해보면,
NFA 에서 q1 상태일 때 a가 들어오면 q1 으로 갈 수 있고, λ를 또 거쳐서 q2 로도 갈 수 있다. (람다는 매번 고려하자!)
반면 q2 상태일 때 a가 들어오면 갈 수 있는 곳이 없으니 공집합이다.
이 둘의 합집합을 생각하면 {q1, q2} 즉 기존에 만들었던 상태로 그대로 되돌아간다.

이번엔 b를 고려해보면, q1에서 b로 가도 q0, q2에서 b로 가도 q0로 가게 된다.
그런데 {q0} 는 이미 존재하는 상태이므로 다음과 같이 작성할 수 있다.

이제 모든 상태에 대해 a, b 모든 심볼의 아웃고잉 엣지가 있으므로 간선은 더 이상 필요하지 않다.
이제 final state 를 결정해주자.
기존의 NFA에서 q1 이 final state 였으므로, q1을 포함하는 state를 final state로 만들어준다.

마지막으로 init state 가 final state 인지 판별하면 된다.
기존의 NFA 에서 λ 입력이 주어졌을 때 final state로 가지 못하므로, q0 는 final state가 아니다.
따라서 위 그래프가 최종적으로 변환한 DFA이다.
이렇게 모든 NFA를 DFA로 변환할 수 있다.
그리고 이로부터 한가지 추가적인 사실을 유추할 수 있다.
지난 글에서 어떤 언어가 regular 하다 라는 것의 정의를 '이 언어를 DFA로 나타낼 수 있다' 라고 하였다.
(즉, DFA가 만드는 언어는 regular 하다.)
그런데 NFA 는 반드시 DFA로 바꿀 수 있으므로,
NFA에 의해 정의되는 언어, NFA가 만드는 언어 역시 regular 하다고 말할 수 있음을 알 수 있다.
'CS > 오토마타' 카테고리의 다른 글
| [오토마타] 7. Regular Expression (0) | 2024.10.23 |
|---|---|
| [오토마타] 6. FA 에서 state 개수 줄이기 (0) | 2024.10.22 |
| [오토마타] 4. DFA (Deterministic Finite Accepter) (0) | 2024.10.17 |
| [오토마타] 3. 오토마톤 (0) | 2024.10.17 |
| [오토마타] 2. Language, Grammar (0) | 2024.10.14 |
