암호학 : 비밀 메세지를 보내는 기법
사이퍼 (chiper) : 원문 메세지의 내용을 훼손하지 않고 메세지의 각 문자를 다른 문자나 기호로 바꾸는 방법
시저 암호
알파벳을 특정 key 숫자만큼 자리 이동시켜 재배열한 글자로 대체

3글자씩 뒤로 밀어서 abby를 deeb로 변환하였다.
이를 문자대신 숫자로 매칭해볼 수도 있다.

그러면 이렇게 3을 더한 값을 사용할 수 있다.
물론 27은 범위를 벗어났으니 26으로 나눈 나머지를 취해서 1로 사용할 것이다.

키 값이 3이라는 것을 서로 알고 있다면, 복호화할 때는 역으로 그 값을 빼서 알파벳을 매칭시킨다.
만약 음수가 나오면 26을 더한 값을 취하면 된다. (-1 + 26 = 25)
시저 암호를 사용하여 비밀 메세지를 주고 받을 때는 2가지 정보를 알아야 한다.
1. 알고리즘 : 알파벳을 이동하는 '시저 암호' 방식을 사용할 것이라는 것
2. 키 : 알파벳을 움직일 칸 수

위와 같은 암호문이 있다고 할 때, 키 값을 모르고 시저암호 방식을 적용하여 복호화할 수 있을까?
지금 공백이 들어있는데, 맨 첫글자는 한글자 쓰고 띄어쓰기가 되어있다.
영어에서 한글자를 쓰고 띄어쓰기를 하는 경우는 관사 a 를 생각할 수 있다.
그러면 결국 키 값을 유추할 수 있으므로 보안상 좋지않다.

그러면 이렇게 띄어쓰기를 없애버리면 어떨까?
이때는 통계적으로 자주 등장하는 알파벳 순으로 매칭해서 복호화를 시도해볼 수 있다.
위 문자열에서 제일 많이 등장한 알파벳과, 통계적으로 제일 많이 등장한 e를 매칭해서 key값을 유추해보는 것이다.
대체 암호

그런데 결국 시저암호는 알파벳의 상대적 순서는 유지된 채로 칸만 이동하므로 키 값만 알아내면 내용을 알아내는 것이 어렵지 않다.
그래서 위 그림과 같이 무작위로 알파벳을 매핑시키는 방법을 사용할 수도 있다.
이때는 키 값이 존재하지 않으므로, 이런 매핑 표 자체를 상대방과 안전하게 공유해야하는 문제가 발생한다.
키워드 암호

그래서 이렇게 키워드를 사용한 방법을 쓰기도 한다.
이 방법은 DAN 이라는 키워드와 이 키워드가 어디서부터 시작할 지 offset을 나타내는 키 문자를 공유한다.
그리고 해당 키 문자에서부터 DAN을 한칸씩 적고, 그 뒤에서부터는 아직 사용되지 않은 알파벳을 순서대로 나열한다.
기존의 단순한 시저암호는 사실 26개의 offset 키를 모두 시도해보면 어렵지 않게 문제를 풀 수 있지만,
이 방법은 키워드와 키 값을 모두 알아야만 해독이 가능하므로 보안이 더 좋아졌다.
비즈네르 암호

비즈네르 암호는 시저암호를 여러 번 적용하는 암호화 알고리즘이다.
먼저 DOG 라는 키워드를 하나 정하고 암호화하려는 문장 위에 나열한다.
처음으로 W 위에 쓰인 D는 a를 d 에 맞춘 것으로 보고 key = 3 으로 암호화한다.
그러면 W가 Z로 암호화된다.
뒤에 있는 모든 문자들도 D에 매핑된 문자들은 key = 3으로 암호화한다.
같은 방식으로
e 위에 쓰인 O 는 A를 O에 맞춘 것으로 보고 암호화하고
l 위에 쓰인 G는 A를 G에 맞춘 것으로 보고 암호화한다.
이 방법은 전체 암호문에 대해서는 빈도 분석이 잘 통하지 않는다는 장점이 있다.
하지만 만약 키워드의 길이를 알면, 첫 번째 문자를 기준으로 암호화된 문자들을 추릴 수 있고,
이 문자들에 대해 '빈도를 활용한 기법' 또는 '브루트 포스'로 26가지를 시도해보면서 키 값을 맞추는 방법을 사용할 수 있다.

키워드의 길이가 모를 때는 반복적으로 등장하는 키워드들의 거리를 통해 키워드의 길이를 유추할 수 있다.
위 그림에서 원문의 the 를 ROT로 암호화 한 문장을 보면 반복적으로 KVX가 나오는 것을 알 수 있다.
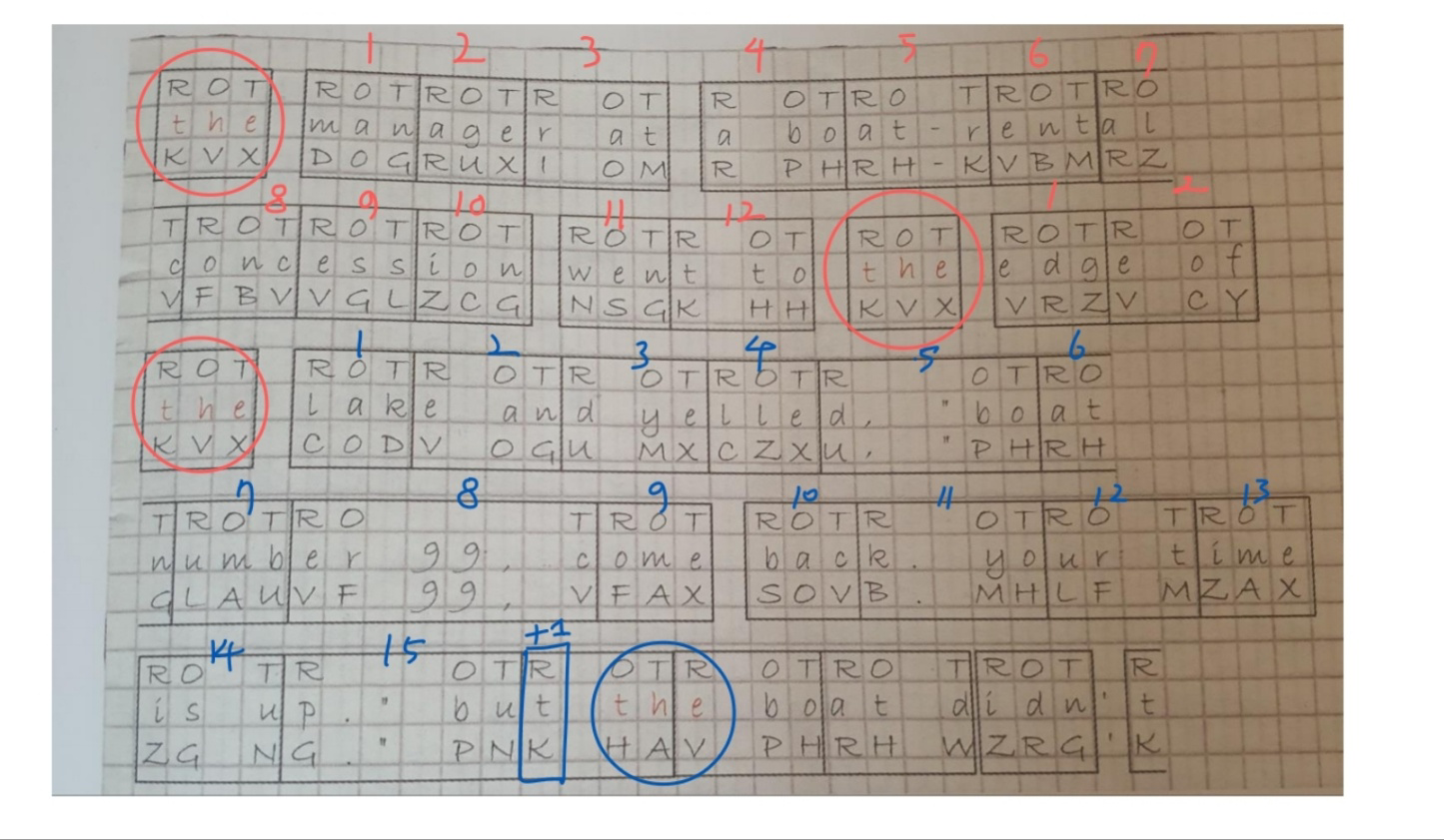
먼저 첫번째 the를 암호화한 KVX 뒤에 동일하게 the를 암호화한 KVX가 나올 때 까지의 거리는 큰 네모 기준 12칸이다.
즉, 36개 문자가 존재한다.
그 다음으로 the를 암호화한 KVX 가 나올 때까지는 2칸 = 6개 문자가 존재한다.
이 둘은 모두 기워드의 길이인 3의 배수이므로 키워드의 길이가 3이라는 것을 계속해서 의심할 수 있다.
즉, 자주 등장하는 암호문의 키워드 간의 간격을 구하고, 이 간격의 공약수를 통해 키워드 길이를 유추할 수 있다.
모듈러 합동

37과 13은 모두 12로 나눈 나머지가 1로 같다.
이렇게 나머지가 같은 두 정수에 대해 mod 12에 대한 모듈러 합동이라고 말한다.
만약 음수에 대해 mod 연산을 한다면, 그때는 양수에 모듈러를 취하고 음수로 바꾼 뒤, 나누는 수를 더해주면 된다.
예를 들어 -20 mod 11 은
20 mod 11 = 9
-9 + 11 = 2
이렇게 나머지를 구한다.
곱 암호
이번엔 모듈러 연산을 이용한 암호화 알고리즘을 알아보자.
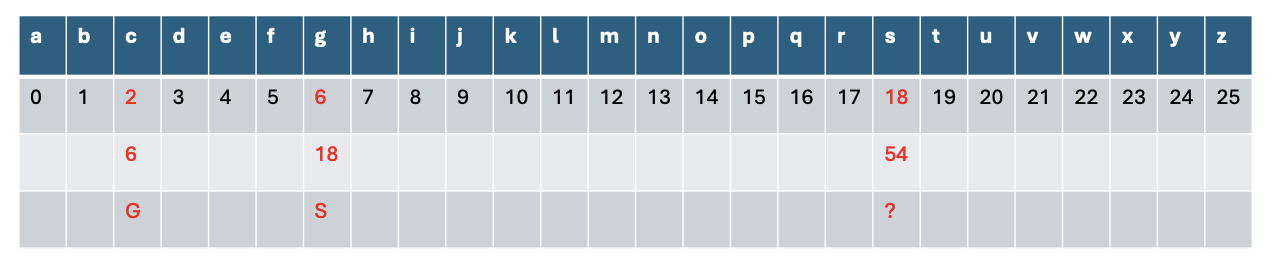
위 그림은 3곱 암호를 보여준다.
알파벳에 0부터 25까지 번호를 매기고, 암호화할 때는 이 수에 3을 곱해서 암호화한다.
만약 위 그림에서 본 것처럼 18과 같이 큰 수라면 26으로 나눈 나머지를 취해준다.
이 나머지 값과 54는 mod 26에 대한 합동으로 같은 수로서 취급하는 것이다.
이때 어떤 수를 곱하는지에 따라 좋은 암호가 될 수도 있고, 나쁜 암호가 될 수도 있다.
위 예시처럼 3곱은 26개 문자에 대해 모두 서로 다른 수가 매핑되므로 좋은 암호이다.
하지만 만약에 2를 곱하면 어떻게 될까?

그림에서 보는 것처럼 M과 U가 모두 중복해서 등장하여 매핑되므로 복호화하기가 어렵다.
따라서 2곱 암호는 좋은 암호가 아니다.

여기에서 '좋은 키'에 대한 고민을 할 수 있다.
좋은 키는 26과 서로소인 값이다.
서로소가 아니라면 위 예시에서 보듯 중복된 매핑이 발생하여 복호화에 문제가 생길 수 있기 때문이다.
하지만 3 mod 26 을 사용한 방법은 영어에만 적용이 가능하고, 다른 문자 체계의 암호화에는 사용할 수 없다.
(당연한 것 아닐까 싶기도..)
그렇다면 곱 암호를 어떻게 해독할 수 있을까?
만약 3곱 암호를 적용한 암호문이 DYSDAS 라고 해보자.
이 값을 숫자로 매핑하면 다음과 같다.
3 24 18 3 0 18
암호화 과정은 3을 곱하고 26으로 나눈 나머지를 취했으므로,
복호화 할 때는 3을 나눠주면 그만이다.
그러면
1 8 6 1 0 3
이 값을 기존 문자로 매핑하면
BIGBAG 이 되어 원래 문자를 알아낼 수 있게 된다.
그런데 만약 FQT와 같은 문자가 들어왔다고 해보자.
F는 숫자로 치환하면 5인데, 3으로 어떻게 나눌 수 있을까?
이제 여기에서 모듈러를 '되돌리는' 방법을 알아야 한다.
암호화 과정에서 숫자에 3을 곱하고 26을 모듈러 취했으니,
복호화 할 때는 26 모듈러를 되돌리고, 3으로 나눠주면 되는 것이다.
여기에서 '모듈러 역원' 의 개념이 등장한다.
즉, 원래의 수 x에 3을 곱하고 26으로 나눈 수가 5일 때, x를 알아낼 수 있으면 되는 것이다.
어떤 수 n의 모듈러 역원 N은 다음을 만족한다.
n x N ≡ 1
따라서 3의 모듈러 역원은 3 x N ≡ 1 을 만족하는 N을 찾는 것이다.
그리고 이를 찾는 간단한 방법은 1부터 26까지 다 대입해보는 것이다.

그 과정은 위와 같다.
따라서 3의 모듈러 역원이 9라는 것을 알 수 있다.
이제 모듈러 역원을 사용해서 암호문을 풀어보자.
어떤 원래의 값이 4였고, 3곱 암호를 적용했더니 12가 되었다.
12로부터 원래의 값을 알아내는 과정은 아래와 같이 연산하면 된다.
12 x 9 = 108
108 % 26 = 4
암호화된 숫자에 역원을 곱하고 26으로 모듈러 연산을 취하는 것이다.
먄약 원래의 값이 5 였다면, 3곱 암호화를 적용하면 15가 되고
15를 다시 5로 복호화 할 때는, 3의 모듈러 역원인 9를 곱해서 26으로 나누면 되므로
15 * 9 mod 26 = 135 mod 26 = 5
로 원래의 값을 얻을 수 있다.
즉, 모듈러 역원이 복호화의 키가 되는 것이다.

모듈러 역원은 이렇게 기존의 3곱 암호표를 사용하여도 구할 수 있다.
암호화 결과가 1이 되는 원래의 숫자가 모듈러 역원이다.
이제 3 이라는 키를 모를 때 어떻게 암호문을 해독할 수 있을지 알아보자.
암호문을 빈도 분석해봤더니 t 라는 문자가 r 로 매핑될 수 있을 것 같다고 해보자.
t = 19
r = 17
따라서 암호화를 할 때는
키 x 19 mod 26 = 17 이었다는 뜻이다.
다르게 표현하면
키 x 19 ≡ 17 (mod 26)
19 에 대한 mod 26 모듈러 역원을 구하면 11 이다.
따라서 키에 19를 곱한 효과를 없애주기 위해 모듈러 합동식 양변에 11을 곱해준다.
키 x 19 x 11 ≡ 17 x 11 (mod 26)
모듈러 연산은 양변에 덧셈, 뺄셈, 곱셈을 해도 합동이 유지된다.
즉, (키 mod 26) x (19 x 11 mod 26) = (17 x 11 mod 26) 이다.
이때 19 x 11 ≡ 1 (mod 26) 이므로
키 ≡ 187 (mod 26)
키 ≡ 5 (mod 26)
로 따라서 키는 5이다.
아핀 암호
아핀 암호는 곱 암호를 한번 더 복잡하게 만든 암호화 알고리즘이다.
원문 숫자 x 에 대해 26과 서로소인 값 m을 곱하고, b 를 더한다.
암호화 키는 (m, b) 이고, 복호화를 할 때는 암호문에서 b를 뺀 뒤 m의 모듈러 역원을 곱하고 mod 26을 취하면 된다.
RSA
소수를 활용한 암호화 알고리즘으로, 어떤 큰 수가 소수인지 아닌지 판별하는데 오래 걸리는 점을 활용한다.
소수 판별
소수를 판별하는 제일 간단한 방법은 2부터 자기 자신까지 나눠보는 것이다.
하지만 이렇게 하면 시간이 너무 오래걸린다.
정수론 개념을 이용하면 이를 조금 더 최적화 할 수 있다.
어떤 수가 1이외의 약수를 갖는다면 모든 약수는 a - b 쌍으로 되어 있기 때문에 a < b 라면 a는 반드시 어떤 수의 제곱근 이하의 수이다.
따라서 소수를 판별할 때는 2부터 자기 자신의 제곱근까지만 나눠보면 소수를 판별할 수 있다.
특히 나눠보는 수가 합성수라면 그 수로는 나눠볼 필요가 없다.
합성수로 나누어 떨어진다면, 그 합성수를 구성하는 소수로 나누어 떨어졌어야 하기 때문이다.
이를 정리하면 소수 판별 방법은 다음과 같다.
어떤 소수를 제곱한 값이 확인하려는 수보다 처음 커지는 소수를 찾는다.
확인하려는 수가 2부터 해당 소수까지의 소수들 중 나누어 떨어지는 소수가 있는지 확인한다.
예를 들어 113이 소수인지 판별해보면
113보다 처음 커지는 소수의 제곱의 11의 제곱이다. (121 > 113)
113은 11, 7, 5, 3, 2로 나누어 떨어지지 않으므로 소수이다.
또 다른 예로 1019가 소수인지 판별해보자.
만약 소수가 아니라면 소인수를 가질 것이다.
40 x 40 > 1019 이므로, 소인수가 있다면 그 소수는 40보다 작을 것이다.
30 x 30 < 1019 이므로, 소인수가 있다면 그 소수는 30보다 클 것이다.
30과 40 사이의 소수는 31과 37이 있으므로 시도해보면
37 x 37 > 1019 이므로 37은 소인수가 아니다.
31 x 31 < 1019 이므로 소인수가 있다면 31보다 크다.
그런데 31부터 37 사이에는 소수가 없으므로 1019를 확인할 때는 31보다 작은 소수에 대해서만 확인하면 된다.
사실 소수는 무한히 많다.
어떤 수 N이 2 x 3 x ... x 37 이런 식으로 소수들이 증가하는 순의 곱으로 구성된 수라고 해보자.
그러면 N+1 은 지금까지 구성된 모든 소수로 나누어 떨어질 수 없다.
따라서 N+1 은 새로운 소수가 된다.
알고리즘
이제 RSA 암호화의 알고리즘을 살펴보자.
먼저 2개의 소수 p, q를 선택한다.
그리고 p-1, q-1 과 모두 서로소인 e를 선택한다.
그러면 n = p x q 라고 할 때, (n, e) 가 공개키가 된다.
예를 들어 2개 소수로 5, 11 을 골랐다면
5-1, 11-1 과 모두 서로소인 e 로 7을 고를 수 있다.
그러면 공개키는 (55, 7) 이 된다.
< 암호화 >
암호화는 원본 메세지가 m 일 때 공개키를 사용하여 다음과 같이 수행한다.
m^e mod n
만약 m = 9 였다면 (알파벳 J에 해당)
9 ^ 7 mod 55 = 4 (알파벳 E에 해당)
< 복호화 >
복호화는 암호 메세지가 C 일 때, 해독키 d에 대해 다음 연산을 수행한다.
C^d mod n
d 는 복호키로서 나 혼자만 알고 있어야 하는 값이다.
이 값은 공개키에 들어있는 e와 mod (p-1)(q-1) 에 대한 모듈러 역원이다.
즉 ed ≡ 1 (mod (p-1)(q-1)) 이다.
한번 e = 7 과 p = 5, q = 11 값을 알고 있을 때 d 를 구해보자.
7d ≡ 1 (mod (5-1)(11-1))
7d ≡ 1 (mod 40)
d에 1부터 쭉 대입해보면 23일 때 7 x 23 % 26 = 1 이 된다.
따라서 D = 23 이다.
아까 위 예시에서 4로 암호화한 값을 복호화해보자.
복호화 공식에 대입하면
4^23 mod 55 = 9 로 원문의 9가 얻어진다.
RSA 암호화의 핵심은 공개키 (n, e) 로부터 n을 구하는데 썼던 p, q를 쉽게 알아낼 수 없다는 것이다.
만약 이를 쉽게 알아낼 수 있다면 복호화 키 d를 위와 같이 계산해낼 수 있게 된다.
이때 (p-1)(q-1) 값에 대해서 모듈러 역원 d를 구할 때, 이 값이 쉽게 구해지지 않을 수 있다.
가령 e는 7 이었는데, (p-1)(q-1) = 180 이었다고 해보자.
그러면 1부터 쭉 d에 대입해서 계산해볼 때 한참동안 안구해질 수 있다.

위와 같은 상황에서 빠르게 역원을 구할 때는 mod 180 의 값이 1이 되는 어떤 수를 찾고, 그 값에 7을 곱했을 때도 여전히 mod 180의 값이 1인이 확인하는 방법으로 빠르게 구할 수 있다.
mod 180 이 1 이라는 이야기는 이 수가 180*Q + 1 꼴이라는 것이다.
이때 180*Q + 1 가 7의 배수라면 180*Q + 1 이 7d 의 꼴로 표현되는 1에 대해 모듈러 합동이므로
이 수를 7로 나누면 우리가 찾는 d 값이 된다.
이제 Q를 1씩 대입해보면서 찾아보자.

구하다보면 180*4 + 1 를 구할 수 있다.
이 수를 7로 나눈 103이 우리가 찾는 역원이 된다.
(이는 중국인의 나머지 정리에서 나온 방법이라고 한다.)
'CS > 기초데이터베이스' 카테고리의 다른 글
| [데이터베이스] 29. RAID (3) | 2024.12.10 |
|---|---|
| [데이터베이스] 28. 보안 응용 (0) | 2024.12.09 |
| [데이터베이스] 26. 정규화 (1NF ~ 5NF) (0) | 2024.12.08 |
| [데이터베이스] 25. 동시성 제어 & 장애 복구 (0) | 2024.12.07 |
| [데이터베이스] 24. 트랜잭션 & 직렬 가능성 (0) | 2024.12.07 |
