흐름을 다시 정리해보면 어떤 문장이 CFG에 포함되는지 판별하기 위해서 파싱을 활용할 수 있는데,
CFG는 너무 자유도가 높아서 파싱 시간이 오래걸리고, 심지어 끝나지 않을 수도 있다.
따라서 이 문제를 해결하고자 지난 글에서는 CFG의 문법을 단순화하기 위해
λ-production, unit-production, useless production 순으로 필요없는 프로덕션을 제거하였다.
이번 글에서는 CFG의 특수한 형태를 갖는 노말 폼 형태의 문법을 통해 간단하게 파싱할 수 있도록 표현하는 방법을 정리한다.
Chomsky Normal Form
모든 production 이 다음 형태를 가지면 참스키 노말 폼이다.
1. A → BC ( A, B, C 는 변수)
2. A → a (a는 터미널)

예를 들어 6.7 예제에서 위의 형태는 참스키 노말 폼이다. (생성하는 2개 변수가 같거나 다른 것에 대한 조건은 없다.)
반면 아래는 변수 하나에서 변수 3개를 생성하거나, 변수 1개가 터미널 2개를 생성하고 있으므로 참스키 노말 폼이 아니다.
이때 모든 λ-free 언어를 생성하는 CFG는 동등한 참스키 노말 폼 형태의 문법을 가질 수 있다.
이는 다음과 같이 변환하면 된다.
1. 기존의 문법을 다음 형태의 프로덕션만 갖는 문법으로 표현한다.
A → a 또는 A → CDE...
이는 지난 글의 simplify 방법을 적용했다면 화살표 오른쪽에 1개만 남는 경우 그것은 반드시 터미널 심볼이고,
여러 개의 터미널과 변수가 뒤죽박죽 섞여 있다면, 터미널 심볼 하나하나를 다 새로운 변수 하나가 produce하도록 고쳐서 변수만 남도록 만들 수 있다.
2. A → CDE ... 형태를 변수를 추가하여 변형한다.
A → CA2
A2 → DA3
A3 → EA4
A4 → ...

예제로 위와 같은 문법을 CNF로 바꿔보자.

이렇게 바꿀 수 있다.
Greibach Normal Form
GNF는 모든 문법의 프로덕션이 다음 형태를 만족하면 된다.
A → aX (이때 X는 0개 이상의 변수나열)
S-grammar랑 유사하지만, S-grammar와 달리 (A, a) 조합이 유일해야 한다는 조건은 없다.

위 문법은 GNF인지 확인하고 아니라면 바꿔보자.
예제 6.9는 GNF이 아니다. S→AB 에서는 터미널이 없기 때문이다.
이는 다음과 같은 형태로 바꿔줄 수 있다.

A가 프로듀스하는 것들을 A자리에 대신 써주면 된다.
이렇게 작성하면 이 문법은 GNF 형태를 만족한다.
하지만 S-Grammar는 아니다.
A 에서 b를 읽었을 때 갈 수 있는 선택지가 2가지, S에서도 b를 읽었을 때 갈 수 있는 선택지가 2가지 있기 때문이다.
예제 6.10 도 GNF가 아님은 쉽게 알 수 있다.
이는 새로운 변수를 추가하면 아래와 같이 쓸 수 있다.

CNF에서 한 것 처럼, 터미널 하나를 변수로 바꿔주면 위처럼 표현할 수 있다.
GNF는 CNF와 마찬가지로 λ-free language를 만드는 CFG에 대해, 모든 CFG를 같은 언어를 만드는 GNF형태의 문법으로 바꿀 수 있다.
CYK 알고리즘
이제 어떤 문장이 CFG 문법으로 표현한 언어에 속하는지 판별하기 위해 파싱하는 방법중 하나인 CYK 알고리즘을 알아보자.
CYK 알고리즘의 전제 조건은 문법이 참스키 노말 폼 형태여야 한다는 조건이 있다.
그리고 이 조건을 만족하려면 앞서 정리한 글의 방법을 사용하여 문법을 simplify 하고, 그 문법을 CNF 형태로 변형해주면 된다.
CYK 알고리즘을 표현하기에 앞서 아래와 같은 정의를 사용한다.
w_ij : 어떤 문자열의 i~j 에 해당하는 substring
V_ij : w_ij를 유도할 수 있는 변수 집합
CYK 알고리즘이 문장을 판별하는 방법은 어떤 문장의 길이가 N 일 때, V_1N 에 S가 들어있는지 확인하는 것이다.
w_1N은 첫번째 문자부터 마지막 문자까지의 서브스트링, 즉 내가 판별하려는 문장 그 자체를 말한다.
따라서 V_1N은 내가 판별하려는 문장 그 자체를 '유도할 수 있는' 변수들 집합에 S라는 시작 변수가 있다면 유도 가능한 것이고, 없다면 유도가 불가능 한 것으로 판단한다.
그렇다면 V1N을 어떻게 확인할 수 있을까?
이 방법은 DP를 사용해서 바텀업 방식으로 점점 키워나가듯 테이블을 채워서 구한다.

예제 6.11 에 해당하는 문장과 문법에 대해 CYK 알고리즘을 적용해보자.
먼저 주어진 문법은 CNF 형태로 되어있어야 하며, 위 예제 문법은 CNF를 만족한다.

먼저 첫번째 단계로 V_ii 를 확인한다.
CNF에서 화살표 오른쪽에 1개의 단위만 존재하는 경우, 그것은 반드시 터미널이므로, 첫 단게는 싱글 터미널을 뽑아내는 변수를 찾겠다는 것과 같다.
먼저 V_11 을 보면 w_11 은 a 이므로, a를 유도할 수 있는 변수 A가 추가된다. S, B는 유도할 수 없다.
같은 방법으로 V_55까지 채우면 아래와 같다.
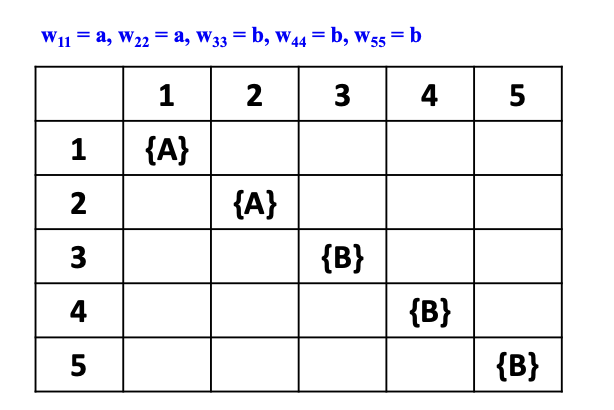
다음 단계로 V_ij 을 확인해보자.
V_ij 에 속하는 변수를 찾는다는 것은
V_ik 에 속하는 변수가 X 이고, V_(k+1)j 에 속하는 변수가 Y 일 때,
A→XY 라는 문법이 존재한다면 V_ij 에는 A가 들어가는 식이다.
이제 스텝 2부터는 간격이 1 차이에서부터 시작하여 점점 증가한다.
먼저 간격이 1 차이일 때는 V_ij = V_i(j-1) 에 있는 변수와 V_jj 에 있는 변수의 조합을 나타내는 변수가 있는지 확인하면 된다.
예를 들어보자. V_12 의 뜻은 w_12를 유도하는 시작 변수들의 집합이라는 뜻이다.
이는 V_11 에 있는 변수와 V_22에 있는 변수에 대한 모든 조합을 살펴보고, 각 조합에 맞는 sentential form을 생성하는 변수가 있는지 확인하면 된다.
위 그림에서 보면 V_11 에는 A 만 들어있고, V_22 에도 A만 들어있다.
이제 V_12를 확인할 때는 X → AA 인 X가 있는지 주어진 프로덕션에서 확인해보면 된다.
그런 production은 없으므로 V_12 에는 공집합이 들어간다.
AB가 바뀌는 경계 V_23을 확인해보자.
V_23 은 V_22 V_33 을 확인해보면 되며, 이는 X → AB 에 해당하는 X가 존재하는지 프로덕션을 확인하면 된다.
그리고 S, B가 X에 해당하므로 V_23 = { S, B } 이다.

그러면 위와 같이 표를 채울 수 있다.
정리하면 V_ij 에 대해서 문자열을 2조각으로 나눠 왼쪽 조각을 유도하는 변수와 오른쪽 조각을 유도하는 변수 집합에 대해
X → <왼쪽 조각><오른쪽조각> 에 해당하는 X 가 있는지 확인해서 변수 집합에 추가하면 되는데,
문자열을 2조각으로 나누는 방법은 문자열의 길이가 n 일 때, n-1 가지 존재하므로
모든 경우의 수를 다 해보면서 체크하면 된다.
수식으로는 V_ij 의 원소는 V_ik V(k+1)j 의 모든 콤비네이션 중 하나라도 생성한다.
이때 k의 범위는 i .. j-1 이다.

스텝 3에서는 이렇게 1개 / 2개 를 유도하는 경우와 2개 / 1개를 유도하는 경우의 수를 조합해보면 된다.
노란색 끼리 조합해보면 X → AS , X → AB 를 하나라도 만족하는 X를 다 찾아서 집합에 추가하면 되며,
AS는 생성하는 변수가 없고 AB는 { S, B } 가 생성하므로 위 그림과 같이 추가할 수 있다.

스텝 4에서는 이렇게 3가지 경우의 수를 해보면 되고

최종 스텝 5는 이렇게 4가지 경우의 수를 해서 변수 집합을 구성하면 된다.
그리고 이렇게 구성된 변수 집합에 시작 변수 S가 들어있다면 이 문자열은 문장이고, S가 없다면 문장이 아니다.
이 알고리즘의 시간복잡도를 계산해보면, 먼저 문자열의 길이가 w일 때, 구성해야 하는 테이블의 크기는 w² 이다.
이때 테이블의 원소 하나를 확인할 때는 1단계에서는 1번, 2단계에서는 1번, ..., w 단계에서는 w-1 번의 확인이 필요했다.
따라서 각 칸을 채우는 단계는 최대 w 번 확인한다고 상한을 그어두면, 이 알고리즘의 빅-O 노테이션은 O(w³) 이다.
'CS > 오토마타' 카테고리의 다른 글
| [오토마타] 19. NPDA & CFL (0) | 2024.12.12 |
|---|---|
| [오토마타] 18. NPDA (0) | 2024.12.11 |
| [오토마타] 16. 문법 변환 - Simplify CFG (0) | 2024.12.08 |
| [오토마타] 15. Parsing (0) | 2024.12.08 |
| [오토마타] 14. CFG & Derivation (0) | 2024.12.04 |
