먼저 결론부터 말하자면,
모든 NPDA로 만들어지는 언어는 CFL이고,
모든 CFL은 그 언어를 만드는 NPDA가 존재한다.
즉, nondeterministic pushdown automata 와 CFL은 equivalent 하다.
이번 글에서는 이를 한 쪽씩 증명해볼 것이다.
CFL → NPDA
CFL의 문법을 normal form 으로 변환하는 과정에서 살펴본 폼중에 GNF가 있었다.
CNF는 파싱하는데 도움을 주었고, CYK 알고리즘에 사용되었다면
GNF는 CFL을 NPDA로 나타내는데 도움이 된다.
모든 λ-free CFL은 그 문법을 GNF 형태로 변환할 수 있다.
GNF로 변환된 문법은 다음과 같이 NPDA로 나타낼 수 있다.
GNF에서 사용되는 프로덕션 A → xB 에 대하여 다음과 같이 표현할 수 있다.
현재 스택의 top에 있는 A 라는 스택 심볼은, x를 읽었을 때, B로 대체될 수 있다.
(즉, A를 빼고 B를 넣을 수 있다.)
이렇게 sentential form에 있는 변수를 스택으로 관리하고
최종적으로 모든 문자를 다 읽었을 때 스택이 비어있으면서 final state에 존재하면 문장이라고 판단할 수 있는 것이다.
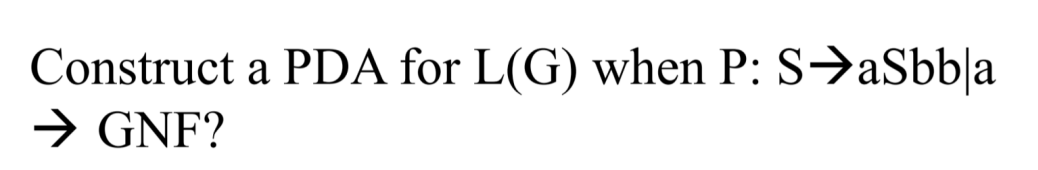
예시를 살펴보자.
위 예시에서 주어진 문법은 GNF 형태를 따르고 있지 않으므로, 먼저 GNF 형태로 고쳐야 한다.

그러면 이렇게 고쳐야 한다.
다음으로 할 일은 스택에 S를 넣어야 한다.

수업시간에는 이렇게 z라는 스택 심볼로 시작해서 S를 추가하는 것으로 표현하셨다.
(그런데 그냥 z대신에 처음부터 S를 갖고 있었다면 어떨까)

나는 이렇게 작성해보았다.
S 에서 aST_bT_b 로 가는 것은 a를 읽었을 때, S를 빼고 대신 ST_bT_b를 넣는 것과 같다고 표현했다.
S 에서 a로 가는 것은 스택에서 S를 뺀 뒤에 아무것도 넣지 않는 것과 같다.
T_b에서 b를 produce 하는 것은 b를 읽었을 때 스택에서 T_b를 뺀 뒤 아무것도 넣지 않는 것과 같다고 표현하였다.
문법을 계속해서 produce 하는 과정은 상태를 유지하도록 하였다.

마지막으로 모든 input symbol을 다 읽었을 때, 스택에 아무런 변수도 남아있지 않다면 문장으로 판별할 수 있다.
(그래서 초기 스택 심볼에 S 대신 z를 넣은 것 같다. S로 시작해서 S가 남았다고 과연 문장을 다 읽었다고 할 수 있는지는 알 수 없기 때문)
이 과정을 거치면 어떤 GNF 형태의 문법이라도 NPDA로 표현할 수 있으므로,
모든 CFL은 같은 언어를 만들어내는 NPDA가 존재함을 증명할 수 있다.

instantaneous description 과 Move를 사용한 표현으로는 위와 같이 표현할 수 있다.

참고로 교수님은 나와는 다르게 풀어주셨다. (GNF를 다르게 만드심)
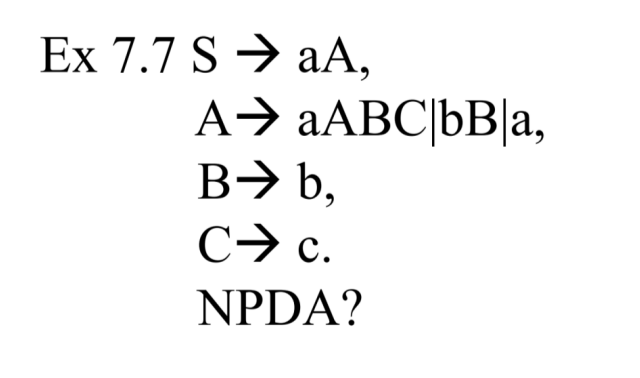
연습문제를 하나 더 풀어보자.
NPDA를 만드는 과정은 다시 정리해보면
1. GNF 로 변환하기
2. S를 추가하는 트랜지션 함수 추가하기
3. 모든 프로덕션에 대한 트랜지션 함수 추가하기
4. 모든 심볼을 읽었을 때 문장인지 판별하는 트랜지션 함수 추가하기
와 같은 과정으로 변환하면 된다.

나는 이렇게 풀었다.
이제 aaabc 라는 문장을 이 문법이 어떻게 처리하는지, derivation 형태와 instantaneous description 형태로 적어보면

이렇게 적을 수 있다.
instantaneous descripton 방식으로 표현할 때, input symbol 이 λ 가 남았더라도 state가 final 이 될 때까지 move를 해주도록 주의하자.
derivation 과정을 살펴보면 GNF의 특징상 leftmost drivation 방식을 사용한다고 했을 때, 센텐셜 폼에서 언제나 왼쪽에는 터미널만, 오른쪽에는 변수만 존재하는 형태이다.
터미널만 존재하는 부분은 terminal prefix 라고 표현하기도 하셨는데, terminal prefix는 기계가 이미 읽은 부분으로 input file에 존재하는 내용이고, 나머지 부분(unprocessed part)은 앞으로 기계가 처리해야 하는 부분으로 스택에 저장되어 있는 (또는 저장될) 부분이라고 생각할 수 있다.
NPDA → CFL
이번에는 임의의 NPDA 기계로부터 CFL을 만들 수 있는지 따져보자.
CFL에서 NPDA를 만들 때, 우리는 상태를 크게 신경쓰지 않고 스택과 input symbol 만 신경써서 만들었기 때문에 크게 복잡하지는 않았다.
하지만 임의의 기계로부터 CFL을 유도할 때는 단순히 거꾸로 하기가 힘든 것이, 기계를 만든 사람이 다양한 상태에 의미를 부여해서 만들었을 수도 있기 때문이다.
이제 기계로부터 CFG를 만들기에 앞서, 편의를 위해 2가지 가정을 먼저 하기로 한다.
1. 스택이 비어있다면 final state로 진입하며, 이때 final state 는 유일하다. (final state는 여러 개 존재할 수 있지만)
이런 가정을 해도 괜찮은 이유는 final state 가 여러 개라면, 이들을 non-final state로 만들고, 새로운 하나의 final state를 만들어서 그곳으로 가는 λ-transition 을 만들어버리면 1번 조건을 만족시킬 수 있기 때문이다.
2. 한번의 transition을 거친 후에는 스택에 있는 원소의 개수가 1개 감소하거나 1개 증가해야 한다.
(즉, 심볼을 푸시하지 않거나, 2개 푸시해야 한다. 하나만 푸시하는 경우는 없다.)
이렇게 가정해도 괜찮은 이유는, 스택에 푸시하는 양의 경우 여러 트랜지션으로 나누면 위 조건을 만족하도록 조절할 수 있기 때문이다.
(하나만 푸시하는 경우에는 0개를 푸시하고 (1개 감소) - 2개를 푸시하는 (1개 증가) 방법으로 나누면 될 것 같다.)
먼저 NPDA에서 CFG를 만들 때 중요한 아이디어는 모든 상태와 스택의 내용을 변수로 만드는 것이다.
이때 한 가지 알아두면 좋은 점은, 문법에서 '변수' 는 특정 시점을 나타내지 않고, 모든 문장을 내포한다.
예를 들어서 S → AB 라는 production이 있다면 이 프로덕션은 단순히 S 라는 변수를 AB로 바꾸는 것이 아니다.
만약 S 라는 변수가 시작변수라면, 이 시작변수 하나는 센텐셜 폼으로써 '문장을 구성하는 모든 문자열' 을 내포하고 있다.
마찬가지로 AB 역시, 둘로 나눠져 있기 때문에 A는 문장의 왼쪽 영역 문자열, B는 문장의 오른쪽 영역 문자열을 내포하고 있다.
이를 생각하면서 다음 내용을 이해해보자.

이제 기계를 나타내는 표현들을 사용하여 production을 만들 때, 그 의미를 이해해보자.
(q0 z qf) →* w 에서 (q0 z qf) 가 통으로 하나의 변수처럼 여겨진다고 생각하자.
위 표현은 q0 상태에서 qf 로 가는 동안 w를 읽었더니, 스택에서 z가 사라졌다는 의미와 같다.
이때 NPDA에서 q0 는 시작 상태, z는 스택의 시작 심볼, qf는 최종 상태이므로 위 말을 해석하면
초기 상태에서 w를 읽어 최종 상태로 갔는데, 그때 (중간에 스택이 어떻게 변화했는지는 모르겠지만) q0 에 분명 z 가 들어있었는데, qf 시점에 가보니 z가 하나 사라져있다고 한다면 위와 같이 production 으로 표현할 수 있다는 것이다.
(q0 z qf 라는 표현이 어떻게 q0 → qf 라는 상태의 이동을 나타내는지는 모르겠어서, 그냥 이렇게 표현한다고 외워야 될 것 같다..)
그림으로는 아래와 같이 표현할 수 있다.

q0 상태에서 스택에는 z가 들어있는 상태로 시작해 w 를 읽었고 모든 인풋 심볼을 다 읽는 move를 거쳤다면,
그때는 qf 상태이고 스택은 텅 비어있었다고 해보자.
이 말은 S 라는 시작변수에서 뭔가 어떻게 derive 했더니 문장이 나왔다는 뜻과 같다고 볼 수 있다.
(시작 상태에서 문자 w만큼 읽는 무브를 거쳤더니 어쨌든 final state로 갔고, 스택도 마침 다 비어있었다.
final state로 갔다는 것 자체가 이미 w가 문장이라는 뜻이지만, 특히 문법으로 표현할 때는 변수를 스택에 저장했었기 때문에 스택이 비어있는 것 역시 문법 관점에서는 중요하다. 또는 위에서 2가지 가정을 할 때, 첫 번째 가정에서 final state로 진입했다는 것은 스택이 비어있을 때 진입하므로 비어있어야 한다고 말할 수도 있다.)

이를 조금 더 일반화 해보면, (qi A qj) 라는 변수에서부터 u 를 유도할 수 있다는 것은,
qi 상태에서 qj 상태로 가는 동안 u를 읽었더니 스택에서 A를 지웠다고 표현할 수 있다.
GNF → NPDA 변환 과정을 살펴보았을 때, A → u 라는 표현을 기계로 나타내면 u라는 심볼을 읽었을 때 스택에서 A를 제거하는 것과 같았다.
그렇다면 (qi A qj) → u 라는 표현은 u 라는 심볼을 읽었을 때 스택에서 (qi A qj) 를 제거하는 것과 같은데,
NPDA 에서 qi, qj 는 상태이므로 스택에 들어있지 않기 때문에, 이 셋 모두를 제거한다는 말은 곧, qi 상태, A 라는 스택 데이터, qj 라는 상태 3가지가 모두 사라진다는 것과 같다.
'상태가 사라진다'는 것을 '상태의 변화'로 이해하면, qi 상태에서 A를 스택에서 팝 했을 때 qj 상태로 변화한다고 볼 수 있다.
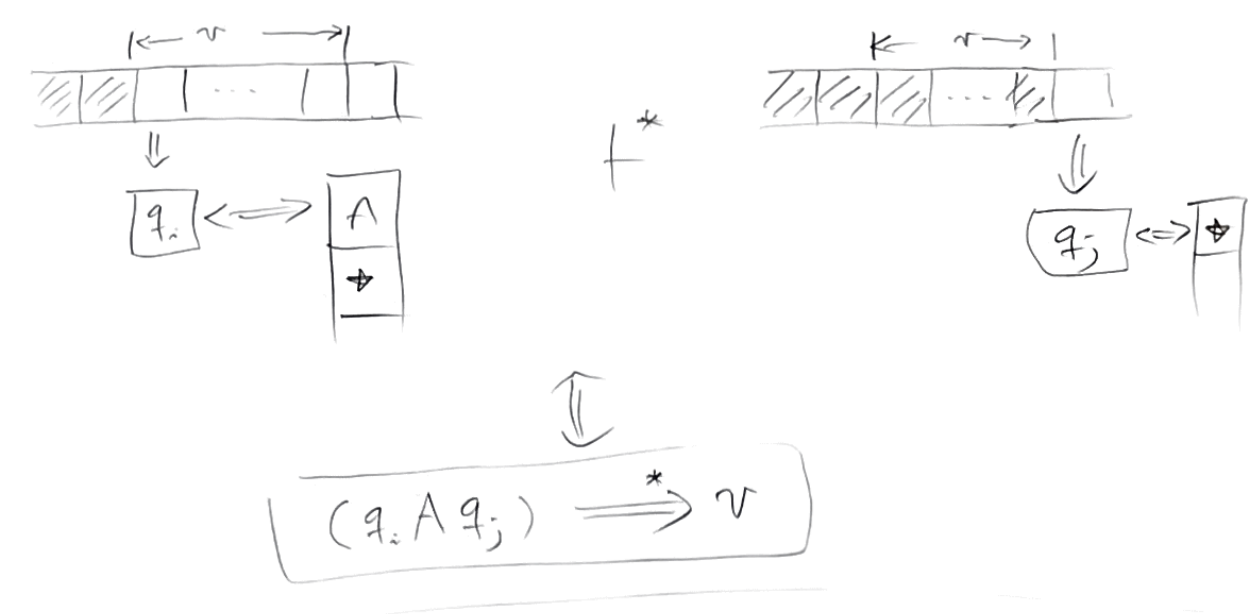
그림으로는 이렇게 표현할 수 있다.
qi 상태, 스택에는 A가 들어있는 상태에서 input symbol 로 v 를 읽었다고 해보자.
몇 번의 move를 거친 최종 결과는 v를 읽고 난 이후의 포인터를 가리키고 있고,
상태는 qj 이며, 스택에는 A하나가 빠진 상황이라는 것이다.
이를 이용하면 트랜지션 함수들만으로도 문법의 production을 정의할 수 있다.

먼저 위의 2가지 가정 중 2번째 가정에 따라, 모든 트랜지션 함수는 스택에 데이터를 푸시하지 않거나, 2개를 푸시한다.
각각의 트랜지션마다 생성하는 문법은 다음과 같다.
1. 스택에 푸시하지 않는 트랜지션 (스택이 1만큼 감소)
qi 에서 a를 읽었을 때, A라는 변수를 스택에서 없애고 qj 상태로 간다.
즉, qi, A, qj 가 사라지는 대신 a 라는 터미널을 읽어냈다고 생각하면
이런 형태는 qi A qj → a 형태로 터미널을 반환하는 문법으로 만들 수 있다.
2. 스택에 2개를 푸시하는 트랜지션 (스택이 1만큼 증가)
qi 에서 a를 읽고 A라는 변수를 팝했을 때, qj 상태로 이동해서 BC를 추가한다.
a 라는 터미널을 얻기 위해서 qi, qj, A를 잃었으며, B C 가 오히려 생겨난 상황이다.
그런데 B C가 생겨났을 때, 이 B, C는 어떤 상태와 함께 없애야 사라질지 모른다. 따라서 모든 상태에 대해서 다 표현을 해준다.
이때 한가지 확실한 점은 트랜지션에서 qi, qj, A 를 잃는 과정에서 현재 상태는 qj 가 되었기 때문에, 스택의 top 에 있을 B를 뺄 때는 qj 상태에서 뺄 것이다.
따라서 B를 제거할 때는 (qj, B, 임의의 상태) 가 사라질 것이다.
그리고 C를 제거할 때는 (임의의 상태, C, 새로운 임의의 상태) 가 사라질 것이다.
그리고 이 과정을 거쳤다는 것은 C를 제거하고 나면 '새로운 임의의 상태' 가 되었다는 뜻이므로
A 라는 변수를 완전히 BC로 대치하고 나면 그때의 상태는 '새로운 임의의 상태' 가 되었을 것이다.
따라서 임의의 상태를 ql, 새로운 임의의 상태를 qk 라고 하면
스택에 2개를 푸시하는 트랜지션 함수는 qi A qk → a (qj B ql) (ql C qk) 형태로 고칠 수 있다.
그리고 qk, ql 은 가능한 모든 상태에 대해 표현해야 추가해야 한다.
(왜 화살표 왼쪽이 qi A qj 가 아닐까?
이는 트랜지션과 produce의 차이에서 발생한다고 이해해보았다.
트랜지션을 통해 스택에서 A라는 변수를 빼고 BC를 넣은 것과, 문법에서 A라는 변수를 제거하고 BC로 바꾼 것은 다르다.
왜냐하면 기계의 트랜지션 함수는 그 순간의 한번 동작을 나타내지만, 분법에서 A를 BC로 대치한다는 것은 그 BC가 앞으로 produce 할 최종 결과물까지 내포한다는 뜻이기 때문이다. 프로덕션은 NPDA관점에서 트랜지션이 아니라 오히려 move 와 비슷하다고 생각하면 좋다.)
위에서 설명한 바에 따르면, qi A qk 는 qi 상태에서 qk 상태로 가는동안 a (qj B ql) (ql C qk) 를 읽었다면 스택에서 A를 하나 지운다는 것과 같다.
B를 왼쪽에 썼기 때문에 , B는 스택의 탑에 존재하고, 다음 단계에서 기계가 동작할 때는 B를 pop 하게 된다.
마지막으로 위 두가지 과정을 거쳐 이렇게 production 들을 정의했을 때,
만약 화살표 왼쪽의 변수 부분이 (q0 z qf) 꼴로 나왔다면, 이 변수는 시작 변수가 된다.
굉장히 어렵다..
한번 예제를 풀어보면서 다시 곱씹어보자.
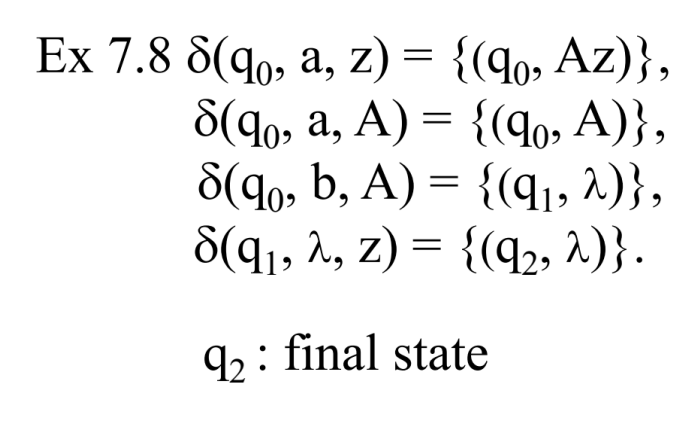
어떤 NPDA의 트랜지션 함수들을 위와 같이 나타내었다.
NPDA로부터 CFG를 만들 때는 위에서 사전에 말한 2가지 가정을 만족하는지 먼저 따져야 한다.
2가지 가정은 다시 복습해보면 다음과 같다.
1. final state로 갔을 때, 스택은 비어있어야 하며, final state는 1개만 존재해야 한다.
위 형태에서 final state는 q2 하나만 있고, q2로 넘어갈 때 스택의 시작 심볼을 읽어서 스택일 텅 비우고 있으므로 이 조건은 만족한다.
2. 모든 트랜지션은 스택의 원소를 1개 감소시키거나, 1개 증가시켜야 한다.
두 번째 트랜지션 함수가 만족하지 않고 있다.
따라서 두 번째 트랜지션을 살짝 변형해주자.
새로운 상태 q3를 만들어서, A를 제거한 뒤 q3 상태로 보내고, q3 에서는 z를 스택에서 뺐을테니 Az를 추가하여 q0으로 되돌아오면 기존의 트랜지션 함수와 같은 동작을 수행한다.

이제 이렇게 변화시킨 5개의 트랜지션 함수가지고 production 들을 만들어보자.
1. 스택을 감소시키는 트랜지션
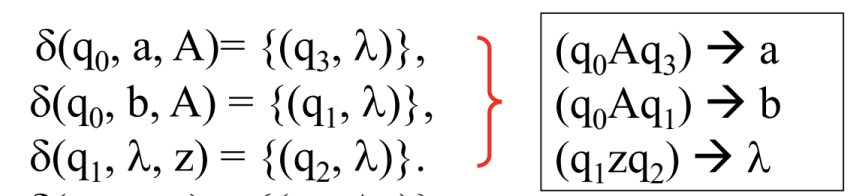
첫 번째 트랜지션 함수를 보면
q0 상태에서 a 라는 심볼을 읽었고, 그때 스택에 A 라는 문자가 들어있었다는 것은
GNF에서 기계로 변환할 때 했던 과정을 역으로 생각해보면 기본적으로는 A → a 로 유도가 되는 상황인데,
여기에 추가적으로 상태의 변화까지 고려해야 하니 A 를 기준으로 상태까지 써줘서
q0 A q3 → a 라고 쓸 수 있다.
위에서 정리한 내용을 기반으로 덧붙이자면, a 라는 터미널을 유도하기 위해서 q0, A, q3 라는 요소가 사용된 것이므로
앞으로 사라져서 없어질 화살표 왼쪾 변수 위치에 q0 A q3 를, 생겨날 a를 오른쪽에 쓴다고 이해해보았다.
세 번째 트랜지션을 보면
q1 상태에서 λ 를 읽었고, 그때 스택에 초기심볼이 들어있었다면,
마치 z → λ 와 같은 프로덕션을 유추할 수 있는데
여기에 상태 변화를 고려해주면 q1 → q2 로 변화하니까
q1 z q2 → λ 와 같이 쓸 수 있다.
2. 스택을 증가시키는 트랜지션

굉장히 복잡한데, 하나만 한번 해보자.
𝛿(q0, a, z) = {(q0, Az)} 라는 트랜지션은
a 라는 터미널 하나를 결정하기 위해, q0, z, q0 라는 상태를 소모하였고, Az 라는 요소가 생겨났다.
기존의 문법 → 기계 변환 과정에서 했던 것을 생각해보면
A → aXY 라는 표현을 기계로 변환할 때는 a를 읽었을 때 A를 스택에서 빼고 XY를 추가하는 형식으로 구현했었다.
일단 상태를 무시하고 스택만 고려해보면
위 트랜지션은 a를 읽었을 때, z를 빼고, Az 를 추가하는 형식이므로
z → aAz 와 같은 문법을 나타내는 것처럼 생각할 수 있다.
이때 상태까지 고려해주면, a라는 터미널을 만들어내기 위해서, z 라는 변수를 소비하려면 q0 에서 q0 로 변화해야만 하기 때문에
위의 표현을 빌리면 (q0, z, q0) 를 소모하여 a 를 얻었으며, Az 도 그 과정에서 얻었다고 볼 수 있다.
그런데 프로덕션은 트랜지션처럼 그 순간 한번으로 끝을 내는게 아니라, 결국 센텐셜 폼을 만드는데 사용되는 것이기에 문장을 내포하고 있어서, Az 를 produce 한다는 표현을 하려면, 화살표 왼쪽의 z 라는 변수를 소비할 때 q0 에서 q0로 변화하는 것이 아니라, q0 에서 Az 를 소비하고 난 최종 상태로 변화해야 한다.
이때 어떤 상태로 최종 변화할지는 알 수 없으므로, 이 기계에 정의된 q0 ~ q3 까지 4개의 상태를 모두 시도해야 한다.
또한 매번 스택에서는 하나씩 변수를 제거하므로, A 를 제거할 때 상태의 변화와 z를 제거할 때 상태의 변화를 모두 기술해주어야 한다.
A를 제거할 때 시작 상태는 화살표 왼쪽의 z를 제거한 이후의 상태에서부터 시작해서 '임의의 상태'로 변화할 것이고
z를 제거할 때 시작 상태는 A를 제거한 이후의 '임의의 상태' 에서부터 시작해서 '새로운 임의의 상태'로 변화할 것이다.
따라서 화살표 z를 제거할 때는 q0 에서 '새로운 임의의 상태' 로 변화하며,
위에서 언급한 '임의의 상태' 와 '새로운 임의의 상태' 는 어떤 것이 될 지몰라서 모든 조합을 다 해봐야 한다.
따라서 16가지 경우의 수를 모두 나열해주면 된다. (....)
16가지를 모두 나열하는 것은 무리가 있기에, 몇 개만 나열해보면
1. 임의의 상태 = q0, 새로운 임의의 상태 = q0
q0 z q0 → a (q0 A q0) (q0 z q0)
2. 임의의 상태 = q1, 새로운 임의의 상태 = q2
q0 z q2 → a (q0 A q1) (q1 z q2)
와 같이 나열할 수 있다.
따라서 위와 같은 과정을 거쳐서 변환하면 모든 NPDA를 CFG로 표현할 수 있기 때문에,
모든 NPDA가 만드는 언어는 CFL 이다.
정리
모든 CFL은 NPDA로 표현할 수 있고, 모든 NPDA가 만드는 언어는 CFL 이다.
CFL → NPDA 로 변환하는 과정은
1. GNF 로 CFG 바꾸기
2. 스택에 Start Variable을 추가하는 트랜지션 함수 만들기
3. 모든 production에 대해 트랜지션 함수 만들기
4. input symbol을 다 읽었을 때 스택이 비어있다면 final state로 가는 트랜지션 함수 만들기
NPDA → CFL 로 변환하는 과정은
1. NPDA 변형하기 (final state는 1개, 이때 final state로 가려면 스택이 비어야 함 + 모든 트랜지션은 스택의 원소가 1개 감소 or 1개 증가)
2. 스택이 감소하는 경우 / 증가하는 경우를 나눠서 프로덕션 작성해주기
3. q0 z qf 형태의 변수는 시작 변수이다.
'CS > 오토마타' 카테고리의 다른 글
| [오토마타] 21. Pummping Lemma (for CFL) (0) | 2024.12.12 |
|---|---|
| [오토마타] 20. DPDA & DCFL (0) | 2024.12.12 |
| [오토마타] 18. NPDA (0) | 2024.12.11 |
| [오토마타] 17. 문법 변환 - Normal Form (0) | 2024.12.10 |
| [오토마타] 16. 문법 변환 - Simplify CFG (0) | 2024.12.08 |
