지금까지 정리한 내용을 다시 정리해보면, 기계학습은 주어진 데이터들을 잘 설명하는 함수(모델)를 찾는 것인데, 함수를 그냥 찾는 것이 쉽지 않아 그 형태를 정해주고, 해당 형태를 결정하는데 필요한 계수를 찾는 문제로 바꾸어 해결한다고 정리할 수 있다.
이때, n차원 공간에 존재하는 데이터를 가장 잘 나타내는 n-1 차원의 직선 또는 하이퍼플레인을 찾는 것이 선형 회귀이다.
이때 '데이터를 가장 잘 나타내는 선형 모델'을 판단하는 기준은 주어진 데이터와 모델 사이의 오차의 합 (=Loss) 이 최소가 되는 모델이고, 선형 모델을 결정하는 변수 (W, b) 에 대한 Loss 값을 나타내는 Loss 함수에 대해 최소값을 찾는 문제로 바꾸어 생각할 수 있다.
최소값을 찾는 제일 간단한 방법은 미분값이 0인 극소값을 찾는 것인데, 미분 값이 0인 지점이 항상 존재하지는 않을 수 있다보니 경사하강법을 통해 미분값이 0에 제일 가까운 지점을 찾는 방법을 사용한다.
이때 극소값이 최솟값이라는 보장은 할 수 없다는 local minimum 문제가 있으나 아직은 해결하지 못 했고, 그럼에도 이 정도에서 만족하여 모델을 찾는다고 한다.
이번 글에서는 이론적으로 살펴본 선형 회귀와 경사하강법을 실제 파이썬 코드로 구현해본다.
먼저, 선형 회귀 문제에서 경사하강법을 사용하는 일반적인 공식은 아래와 같이 계산할 수 있다.
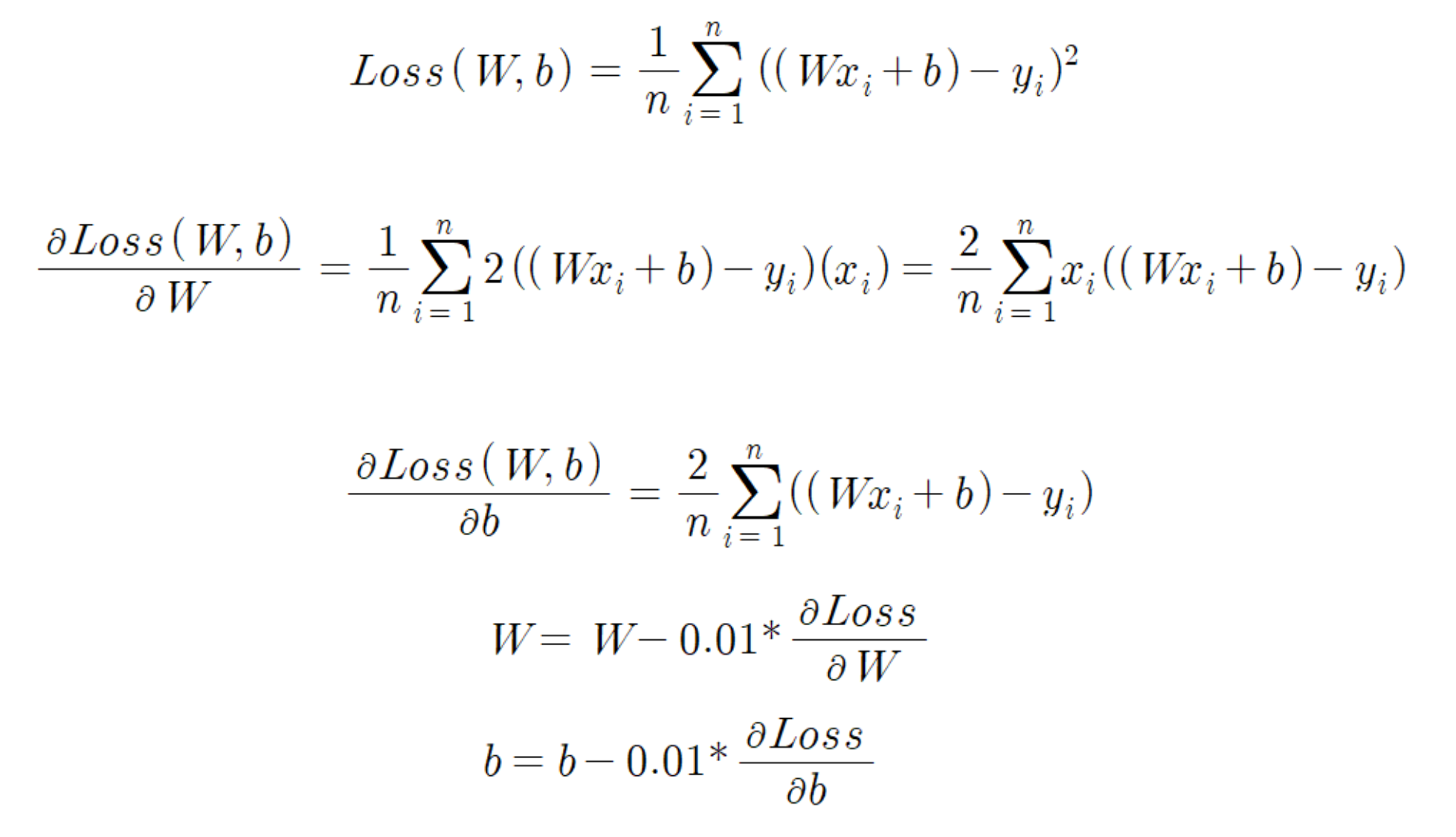
먼저 Loss 함수는 위와 같이 주어진 모델에 대한 모든 Loss 의 제곱 오차의 합으로 정의한다.
(1/n 은 해도 되고 안해도 된다.)
Loss 함수의 최소값을 찾기 위해서 Loss 함수를 W 와 b 에 대해 각각 미분하여, 그 지점이 0에 가까워지는 W, b 를 찾는 과정을 반복한다.
먼저 Loss 함수식 W에 대해 미분하면, 모든 x, y 입력 데이터에 대해 2(Wx + b - y)(x) 의 합으로 나타낼 수 있다. (겉미분 x 속미분)
b에 대한 미분 결과도 마찬가지로 계산할 수 있다.
경사하강법은 반복적으로 이 미분값 (기울기) 을 활용하여 그 다음의 W, b 값을 추론하는 방법인데, 이때 다음 W, b 값은 현재 구한 미분값(기울기)의 반대 방향으로 일정 Learning rate 만큼의 비율로 이동한다.
위 예시에서는 0.01 의 learning rate 를 사용하였다.
그리고 미분값을 구하여 W, b 를 찾는 과정을 계속 반복하다가 미분값이 특정 값보다 작아지면 (이 특정값을 threshold 라고 한다.) 반복을 멈추면 된다.
예제 1
import numpy as np
import matplotlib.pyplot as plt
X = np.array([0.0, 1.0, 2.0])
Y = np.array([3.0, 3.5, 5.5])
한번 간단한 예시로, (0, 3) (1, 3.5), (2, 5.5) 3개 점에 대한 선형 회귀 문제를 경사하강법으로 풀어보자.
입력값 x 는 1차원 벡터, 출력값 y 도 1차원 벡터이므로, y = Wx + b 에서 W, b도 1차원 벡터값이 된다.
W, b = 0, 0
learning_rate = 0.01
epochs = 1000
먼저 W, b 값을 각각 0으로 설정해둔다. (랜덤값을 써도 된다.)
learning rate 는 0.01 로, W, b 값을 업데이트할 반복 횟수 (=에포크) 는 1000 번으로 설정하였다.
input_size = float(len(X))
# Gradient Descent
for i in range(epochs):
y_pred = W * X + b
deltaW = (2/input_size) * sum(X*(y_pred - Y))
deltab = (2/input_size) * sum(y_pred - Y)
W = W - learning_rate * deltaW # update W
b = b - learning_rate * deltab # update b
print(W, b)
이제 에포크만큼 반복하면서 위 수학 공식을 그대로 적용해주면 된다.
모든 입력 데이터에 대해 반복하면서 연산을 하기 보다, 입력 데이터를 행렬로 만들어 행렬 연산으로 한번에 계산하였다.
이 연산은 넘파이를 사용하면 간편하게 할 수 있다.
print(W, b)
y_pred = W * X + b
plt.scatter(X, Y)
plt.plot([min(X), max(X)], [min(y_pred), max(y_pred)], color='red')
plt.show()
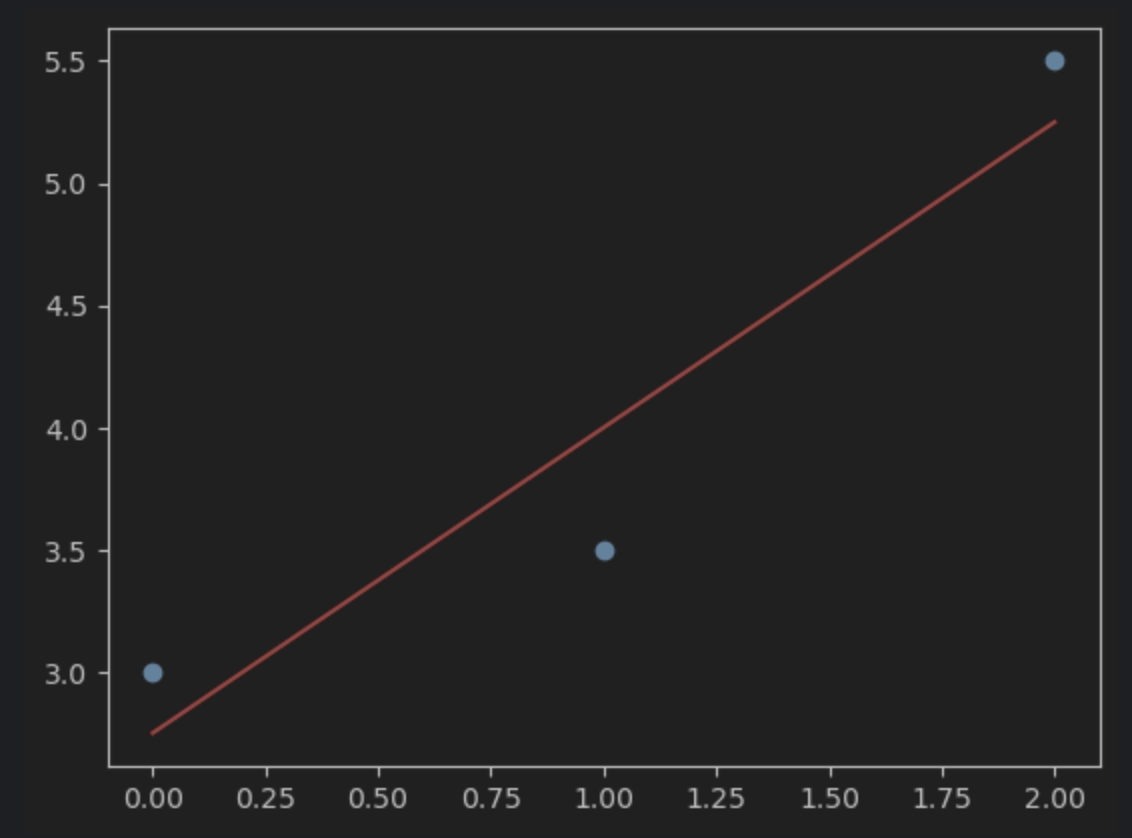
최종적으로 구한 W, b 값과 해당 W, b 값이 나타내는 직선을 그려보면 아래와 같이 나온다.
예제 2
위에서는 수학적으로 구한 공식을 이용해서 직접 손수 계산하여 경사하강법을 구현했다면, scikit learn 라이브러리를 사용하면 간단하게 경사하강법을 구현할 수 있다.
import matplotlib.pylab as plt
from sklearn import linear_model
reg = linear_model.LinearRegression()
X = [[0], [1], [2]]
Y = [3, 3.5, 5.5]
reg.fit(X, Y)
먼저 사이킷런 라이브러리에서 선형회귀 모델을 가져온다.
그리고 이 모델에 위에서 사용했던 데이터를 넣어 함수를 찾는다. (=모델을 학습시킨다.)
이때, X 입력값은 2차원 배열로 넣어야 한다.

학습한 모델로부터 기울기와 y절편 값을 출력해보면 위와 같이 나온다.
이전 예제에서 직접 학습했던 결과값과 비슷한 값이 나온 것을 알 수 있다.
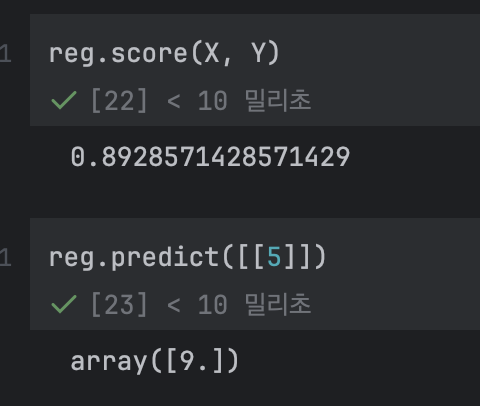
기존의 훈련용 데이터에 대한 점수를 계산하면 0.89 가 나온다. (89%의 정확도를 말하는 듯하다.)
5라는 입력값을 넣어보면 9 라는 예측값이 나온다.
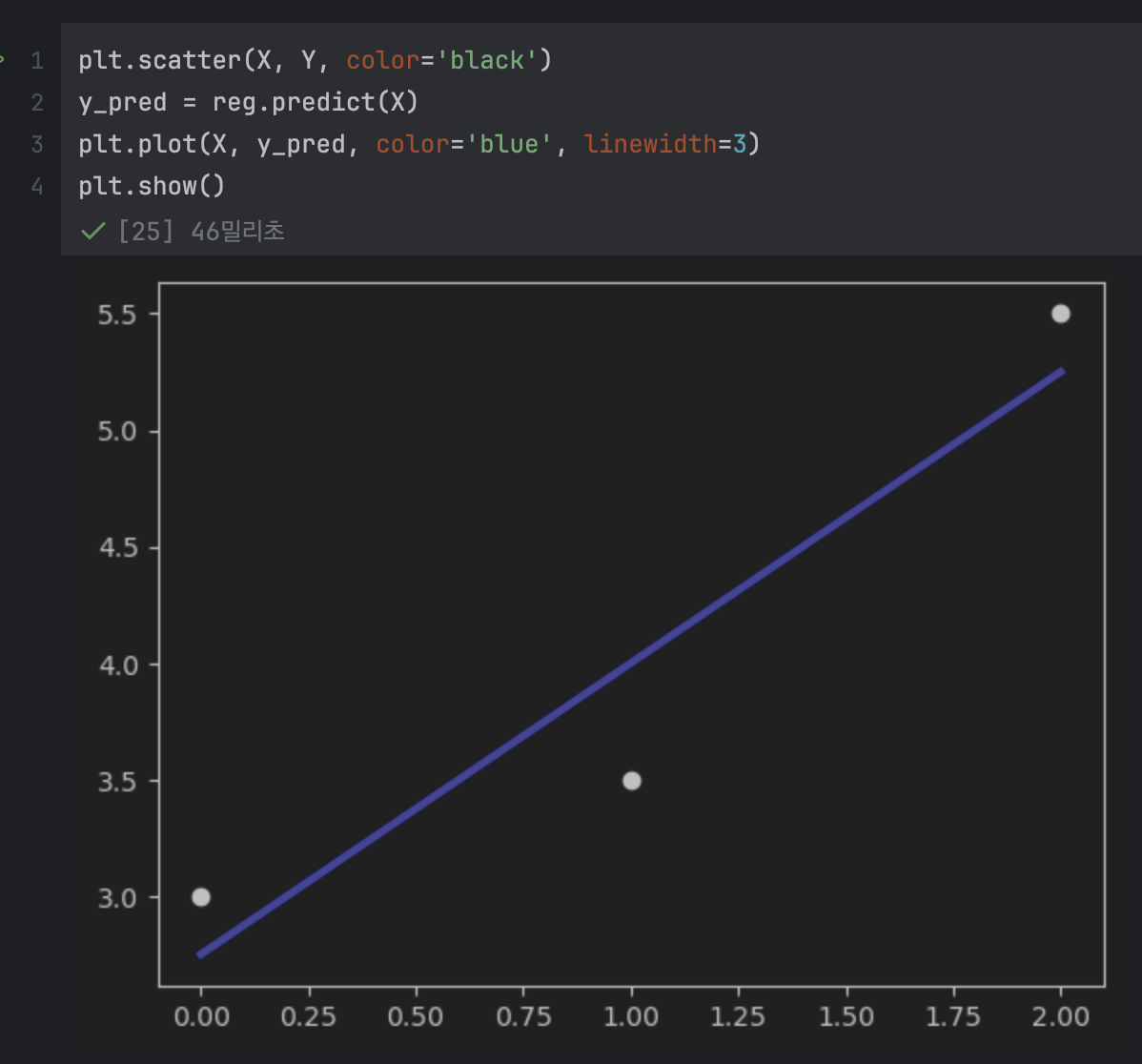
그래프를 그려보면 위와 같으며, 이전에 봤던 그래프와 비슷한 것을 알 수 있다.
예제 3

위와 같은 키-몸무게 데이터가 있다고 해보자.
이 데이터를 기반으로 키가 주어졌을 때 몸무게를 예측하는 모델을 만들어보자.
키와 몸무게 데이터는 키가 증가할수록 몸무게가 증가하는 경향이 있다는 것을 경험적으로 알고 있으므로, 선형 모델을 사용하면 성능이 잘 나올 것이라고 예측해볼 수 있다.
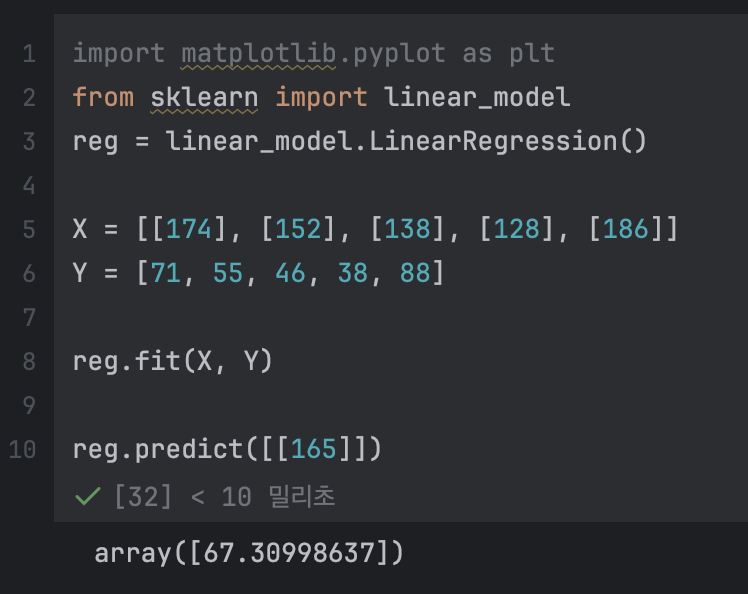
import matplotlib.pyplot as plt
from sklearn import linear_model
reg = linear_model.LinearRegression()
X = [[174], [152], [138], [128], [186]]
Y = [71, 55, 46, 38, 88]
reg.fit(X, Y)
reg.predict([[165]])
사이킷 런을 사용하면 위와 같이 모델을 만들 수 있다.
165cm 를 입력으로 넣으니 67kg 의 몸무게를 예측하였다.

그래프로 나타내면 위와 같이 보인다.
정리하면 지도 학습은 회귀 문제와 분류 문제를 푸는데 사용할 수 있다.
그 중에서 회귀 문제를 풀 때 선형 모델을 사용하는 '선형 회귀' 는 선형 함수의 기울기와 절편을 찾아 모델을 학습시킨다.
이 선형 모델은 1차원 입출력데이터인 경우엔 직선이 나오겠지만, 차원이 높아질 수록 평면, 초평면 등으로 뻗어나가기도 한다.
선형 회귀는 모델과 훈련용 데이터 사이의 오차 합인 Loss 를 최소화하는 모델을 찾는 것이다.
그리고 Loss를 최소화하는 값을 찾는 방법으로 경사하강법을 일반적으로 사용한다.
'CS > 기계학습심화' 카테고리의 다른 글
| [기계학습심화] 6. KNN 구현 (4) | 2025.04.17 |
|---|---|
| [기계학습심화] 5. KNN & Hyperparameter (0) | 2025.04.15 |
| [기계학습심화] 4. 경사하강법의 확장 & SGD (1) | 2025.04.13 |
| [기계학습심화] 2. 선형 회귀 & 경사하강법 (0) | 2025.04.11 |
| [기계학습심화] 1. 기계학습 개요 (0) | 2025.04.10 |
