지난 글에서는 트리와 이진트리, 그리고 이진 트리를 만들 수 있는 가짓수인 카탈란 수에 대해서 정리하였다.
이번 글에서는 이진 트리를 순회하는 3가지 방법을 정리해보고자 한다.
사람에 관점에서는 이진트리의 전체적인 모습이 보이기 때문에 특정 노드를 찾을 때 전체 이진트리에서 특정 노드를 바로 딱 보면 쉽게 알 수 있다. (글로벌 뷰)
하지만 컴퓨터 입장에서 이진트리를 탐색할 때는, 연결리스트 때와 비슷하게, 현재 자신이 보고 있는 노드 T와,
그 T의 ITEM(T), 왼쪽 노드 LEFT(T) , 오른쪽 노드 RIGHT(T) 만 본다. (로컬뷰)
이런 로컬 뷰가 재귀적으로 반복되기 때문에, 이진트리를 탐색할 때는 재귀를 이용하게 되는데, 이진 트리를 재귀적으로 탐색하는 방법에는 3가지가 있다.
Preorder (전위 탐색)
전위 탐색은 현재 노드를 방문하여 데이터를 처리한 뒤, 왼쪽 노드 -> 오른쪽 노드를 방문한다.
Visit the root
Traverse Left subtree
Traverse RIght subtree
간단하게 V L R 로 표시할 수 있다.
이를 수도코드로 표현하면 아래와 같다.
preorder(t) {
if (t == null)
return;
visit(t)
preorder(left(t))
preorder(right(t))
}Inorder (중위 탐색)
중위 탐색은 왼쪽 노드를 먼저 방문한 뒤, 현재 노드를 방문하고, 오른쪽 노드를 방문한다.
Traverse Left subtree
Visit the root
Traverse RIght subtree
간단하게 L V R 로 표시할 수 있다.
수도코드로는 아래와 같다.
preorder(t) {
if (t == null)
return;
preorder(left(t))
visit(t)
preorder(right(t))
}Postorder (후위 탐색)
후위 탐색은 왼쪽 노드를 방문하고, 오른쪽노드를 방문하면, 자기 자신을 방문한다.
Traverse Left subtree
Traverse RIght subtree
Visit the root
간단하게 L R V 로 표시할 수 있다.
수도코드로는 아래와 같다.
preorder(t) {
if (t == null)
return;
preorder(left(t))
preorder(right(t))
visit(t)
}각 순회 방법의 의미
각 탐색 방법들마다 특징이 있다.
먼저 전위 탐색의 의미부터 생각해보자.
아래와 같은 수식이 있다.
1 + 2 * 3 + 4 * 5
이 수식을 피연산자와 연산자로 쪼개서 이진 트리에 넣는다고 생각해보자. (이를 Parse Tree 라고 한다.)

이제 이 Parse Tree 를 전위 탐색해보자.
그러면 아래와 같은 결과가 나온다.
+ + 1 * 2 3 * 4 5
이와 같은 표기식을 전위 표기식라고 하는데, 알아보기가 쉽지는 않다.
하지만 이렇게 함수처럼 표기를 하면 익숙하게 보인다.
add( add( 1, mul(2, 3) ) , mul (4, 5) )
이렇듯 전위 탐색은 마치 함수의 콜스택을 쌓는 것과 비슷한 방법으로 탐색한다.
이번엔 중위탐색의 의미에 대해 생각해보자.
당연하게도 저 Parse Tree 를 중위탐색하면 우리가 아는 " 1 + 2 * 3 + 4 * 5 " 이 식이 그대로 다시 나오고,
이런 표기식을 중위 표기식이라고 한다.
하지만 중위 탐색은 이진 탐색 트리에서 그 진가를 발휘한다.
이진 탐색 트리는 서로 부모-자식 관계인 모든 임의의 두 노드에 대해서,
만약 자식 노드 <= 부모 노드 이면 자식 노드는 왼쪽 자식노드이고,
부모 노드 < 자식 노드 이면 자식 노드는 오른쪽 자식 노드로 오도록 구성한 이진 트리를 말한다.
따라서 어떤 임의 노드에 대해, 그 노드의 왼쪽 서브트리에 있는 모든 자식들은 그 노드보다 작거나 같고,
그 노드의 오른쪽 서브트리에 있는 모든 자식들은 그 노드보다 크다.
이제 1부터 8까지 숫자로 구성된 이진 탐색 트리가 있다고 해보자.
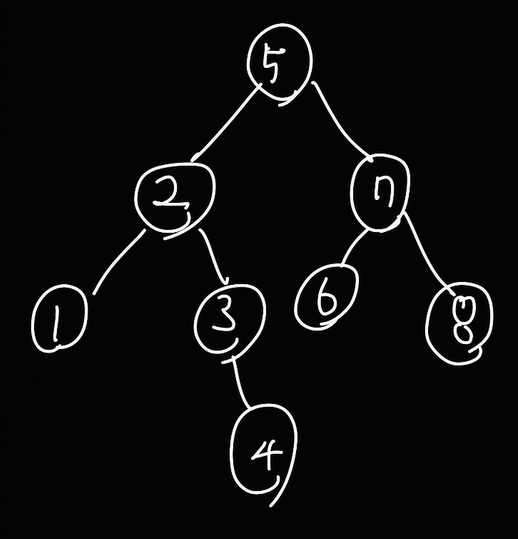
이진트리를 그리는 방법은 다양하겠지만 위와 같은 예시로 그려보았다.
이제 이 이진트리를 중위 탐색해보면 결과가 어떻게 나올지 살펴보자.
1 2 3 4 5 6 7 8
놀랍게도 무작위로 배치된 듯 보이는 숫자가 순차적으로 오름차순 정렬되어 나온다.
이 처럼 이진 탐색 트리에서 중위 탐색으로 모든 노드를 순회하면, 이진 탐색 트리의 모든 노드가 정렬되어 출력된다.
마지막으로 후위 탐색의 의미에 대해 생각해보자.
아까 전위 탐색 예시에 사용했던 트리를 후위 탐색하면 아래와 같이 결과가 나온다.
1 2 3 * + 4 5 * +
이런 식을 후위 표기식이라고 한다.
이런 후위 표기식은 사람이 보기에는 쉽지 않지만, '스택 머신' 이라는 기계 입장에서는 실행하기 좋은 명령어 집합과 같다.
스택머신은 위 식을 입력으로 주면 아래와 같이 동작한다.
1. 만약 숫자가 들어오면 push 한다.
2. 만약 연산자가 들어오면 pop을 두번 하고 연산 결과를 push 한다.
3. 만약 eof 가 들어오면 pop을 한번 하고 출력한다.
위 과정을 따라 계산을 해보자. 연산자를 만나는 순간 끊어보았다.
[ 1 2 3 * ]
숫자는 쭉 push push 하다가 곱셈 연산자를 만나면 pop을 두번 하고 곱셈을 수행한 뒤 결과를 다시 push 한다.
[ 1 6 ]
그 결과 1, 6이 스택에 남아있다.
[ 1 6 + ]
덧셈이 들어왔으니 2번 pop 해서 연산해주고 다시 push 하면
[ 7 ]
7이 남는다.
다시 쭉쭉 숫자를 push 해준다.
[ 7 4 5 * ]
* 연산이 들어왔으니 2개를 빼고 연산한 값을 push 해준다.
[ 7 20 ]
20이 새로 들어오고
[ 7 20 + ]
새로 들어온 + 연산자까지 처리해주면
27
27로 의도한 계산 결과 값이 나온다.
지금까지 이진 트리의 탐색 방법인 preorder, inorder, postorder 에 대해 정리하였다.
다음 글에서는 이진 트리의 응용인 '이진 탐색 트리' 에 대해 정리한다.
'CS > 자료구조' 카테고리의 다른 글
| [자료구조 및 프로그래밍] 10. BST 탐색 시간과 Height 사이 관계 (0) | 2023.10.23 |
|---|---|
| [자료구조 및 프로그래밍] 9. 이진 탐색 트리 (3) | 2023.10.22 |
| [자료구조 및 프로그래밍] 7. 트리와 이진트리 (0) | 2023.10.20 |
| [자료구조 및 프로그래밍] 6. 메모리 관리 시스템 (0) | 2023.10.18 |
| [자료구조 및 프로그래밍] 5. Stack & Queue With Linked List (0) | 2023.10.17 |
