이진 탐색 트리 (Binary Search Tree, BST) 는 노드가 정렬되어 있어 탐색을 수행할 수 있는 이진 트리를 말한다.
각 노드는 여러개의 필드로 이루어진 데이터를 가지고 있다고 가정한다.
데이터 중에서 탐색을 하기 위해 사용되는 데이터를 '키' 라고 한다.
node v 의 키를 key(v) 라고 정의하면, BST 는 모든 노드 u 에 대해서 아래를 만족하는 이진트리이다.
(1) 만약 v 가 u 의 왼쪽 서브트리에 있다면 key(v) <= key(u) 이다.
(2) 만약 v 가 u 의 오른쪽 서브트리에 있다면, key(v) > key(u) 이다.
등호는 좌, 우 둘 중 하나 어디든 들어가도 되지만, 왼쪽에 들어간 것으로 생각하자.
이 정의를 통해 이진 탐색 트리는 매우 효율적으로 원하는 key 를 탐색할 수 있다.
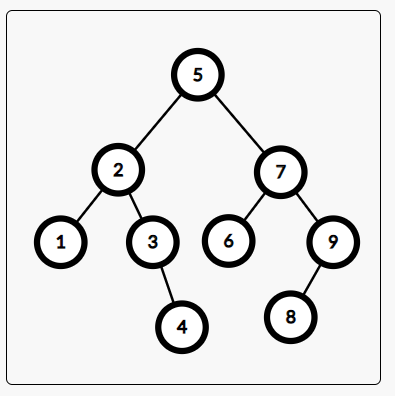
이제 이렇게 생긴 BST가 있다고 가정해보자.
이 트리에서 3이라는 값을 찾는다면 루트인 5에서부터 탐색을 시작한다.
5와 3을 비교하면 3이 더 작으므로 3은 왼쪽 서브트리에 있다. 따라서 왼쪽 노드를 타고 내려간다.
2와 3을 비교하면 3이 더 크므로 3은 오른쪽 서브트리에 있다 따라서 오른쪽 노드를 타고 내려간다.
3을 발견하였다.
만약 트리 안에 없는 키 (예를 들면 2.5) 를 탐색한다고 해보자.
2.5 와 5 를 비교하면 2.5 <= 5 이므로 왼쪽 서브트리로 넘어가고
2.5 와 2 를 비교하면 2.5 > 2 이므로 오른쪽 서브트리로 넘어가고
2.5 와 3 을 비교하면 2.5 <= 3 이므로 왼쪾 서브트리로 넘어가고
왼쪽 서브트리는 공집합이므로 2.5는 없는 값임을 알 수 있다. (이진 트리에 공집합이 포함되어 있는 이유)
이처럼 탐색을 하면서 서브트리를 선택할 때마다 반대쪽 서브트리를 탐색하지 않게 되므로
마치 이분탐색처럼 탐색 데이터가 반 씩 줄어드는 효과가 있다.
만약 연결 리스트나 배열에서 특정 값을 찾고자 할 때는 최악의 경우 모든 데이터를 탐색해야 하므로 O(n) 의 단계가 걸린
다. (배열의 경우 만약 키 값이 정렬 되어 있다면 이분 탐색으로 O(log n) 시간에 찾을 수 있기는 하지만)
이제 BST 에서 search, add, delete 하는 과정을 코드로 작성해보자.
탐색은 위에서 말한 단계를 그대로 구현해내면 된다.
T 는 현재 탐색중인 BST의 루트를 가리키는 포인터라고 하자. (BST 의 서브트리도 BST 이다.)
search(T, find) {
if (T = ^) {
return null // FAILURE!
}
if (Key(T) = find) {
return T // return found node
}
if (Key(T) < find) {
return search( LEFT(T), find )
} else {
return search( RIGHT(T), find )
}
}하지만 이렇게 재귀를 사용하지 않고 반복문으로도 원하는 값을 찾을 수 있다.
함수 내부의 코드가 반복문 한 사이클에서 실행되는 것으로 보면 된다.
find(key) {
T <- head
while (T != ^) {
if ( ITEM(T) == key )
break
if ( ITEM(T) < key )
T <- LEFT(T)
else
T <- RIGHT(T)
}
return T
}이번엔 add 하는 과정을 정리해보자.
add 할 때는 search 하듯이 먼저 add 할 키를 찾는다.
차이점이 있다면, 자신과 같은 수를 발견하면 그 즉시 멈추는게 아니라 그때도 왼쪽으로 계속 타고 내려가야 한다.
그렇게 쭉쭉 내려가다가 더이상 내려갈 수 없는 null 을 만나면 그 곳이 새로 추가될 위치이다.
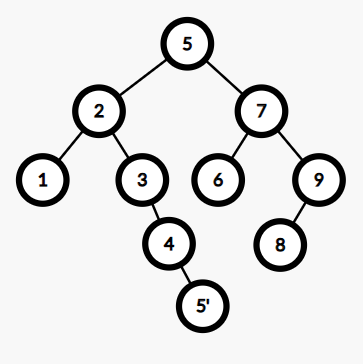
만약 우리가 본 예시 BST에서 5를 추가한다면 아래와 같이 추가될 것이다.
똑같은 5 여도 서로 다른 위치에 존재할 수 있다.
add(key) {
p: now node
q: previous node
p <- T
q <- NULL
while (p != ^) {
if (key <= ITEM(p)) {
q <- p
p <- LEFT(p)
} else {
q <- p
p <- RIGHT(p)
}
}
// 이곳에서는 p 가 Null 이다.
r <- NEW()
if (r == ^)
return // ALLOC_ERR
ITEM(r) <- key
LEFT(r) <- ^
RIGHT(r) <- ^
if (T = NULL) { // BST 가 비어있을 때를 고려하자.
T <- r
} else if (key <= ITEM(q)) {
LEFT(q) <- r
} else {
RIGHT(q) <- r
}
}코드로 구현하면 위와같이 구현된다.
하지만 이 코드는 귀찮은 부분이 많다.
빈 트리인 경우를 고려해서 add 를 짜야하고, 이전 노드를 계속해서 저장해야한다.
이런 부분을 개선하기 위해 아래와 같은 키워드를 사용해 개선해보자.
LOC(p) : p 라는 공간의 주소 ( C언어의 &p )
CONTENT(p) : p 라는 공간의 데이터 ( C언어의 *p )
그러면 아래와 같은 구현이 가능하다.
add(key) {
// search key pos
p <- T
q <- LOC(T) // T 라는 '포인터 변수'의 주소값 (포인터의 포인터)
while( p != Null) {
if (key <= ITEM(p)) {
p <- LEFT(T)
q <- LOC(LEFT(T))
} else {
p <- RIGHT(T)
q <- LOC(RIGHT(T))
}
}
// 이 시점에는 p 가 반드시 Null 이다.
r <- NEW()
if (r == NULL)
return // MEMORY_ALLOC_ERR
ITEM(r) <- key
LEFT(r) <- Null
RIGHT(r) <- Null
CONTENT(q) <- r
}만약 비어있는 BST 였다고 해보자.
그렇다면 p 에는 Null 이 들어가면서 반복문을 돌지 않고 바로 나온다.
이때 q 는 포인터 변수 T 그 자체를 가리키고 있으므로, CONTENT(q) <- r 을 통해
새로 생성한 노드의 주소를 포인터 변수 T 에 직접 넣을 수 있다.
이번엔 이를 재귀로 구현해보자.
T: pointer of pointer for BST
add(T, key) {
if( CONTENT(T) == NULL ) { // add 할 위치 발견
CONTENT(T) <- NEW() // CONTENT(T) 는 이전 노드의 Left 든, Right 든 확정한 Link 공간 자체
// 이 코드 덕분에 이전 노드를 판단할 필요가 없다.
if( r == NULL ) {
return // MEMORY_ALLOC_ERR
}
ITEM(r) <- key
LEFT(r) <- NULL
RIGHT(R) <- NULL
} else if ( key <= ITEM(CONTENT(T)) ) {
add(LOC( LEFT( CONTENT(T) ) ), key)
} else {
add(LOC( RIGHT( CONTENT(T) ) ), key)
}
}이해하기가 조금 복잡해졌지만, 대신 구현이 아주 깔끔해졌다.
T는 포인터 변수의 공간을 가리키기 때문에 CONTENT(T) 로 포인터 변수의 값을 읽어야 한다.
이제 마지막으로 이진 탐색트리의 '삭제' 부분을 구현해보자.
삭제를 구현할 때는 3가지 경우를 생각해보아야 한다.
1) 삭제할 노드의 degree 가 0 인 경우
>> 부모노드와 링크를 끊고, 그 노드를 삭제하면 된다.
2) 삭제할 노드의 degree 가 1 인 경우
>> 부모노드와 링크에 자신의 자식 노드를 넣고, 자신은 삭제하면 된다.
3) 삭제할 노드의 degree 가 2 인 경우
>> 삭제할 노드의 Successor 를 찾아 Successor 로 삭제할 노드를 대체하고,
원래 Successor 위치는 Successor 의 Right 자식 노드로 대체한다.
Successor 는 삭제할 노드의 바로 다음 큰 노드를 의미하며, 이는 삭제할 노드의 오른쪽 서브트리 내 값 중 제일 왼쪽에 위치한 노드이다.
삭제 부분은 구현이 복잡하기 때문에 코드 구현은 생략한다.
지금까지 BST에 대한 내용을 정리하였다.
다음 글에서는 BST에서 특정 노드를 찾기 위한 비교횟수를 정리하고자 한다.
'CS > 자료구조' 카테고리의 다른 글
| [자료구조 및 프로그래밍] 11. 우선순위 큐와 Heap (0) | 2023.12.02 |
|---|---|
| [자료구조 및 프로그래밍] 10. BST 탐색 시간과 Height 사이 관계 (0) | 2023.10.23 |
| [자료구조 및 프로그래밍] 8. 이진 트리의 순회 (0) | 2023.10.22 |
| [자료구조 및 프로그래밍] 7. 트리와 이진트리 (0) | 2023.10.20 |
| [자료구조 및 프로그래밍] 6. 메모리 관리 시스템 (0) | 2023.10.18 |
