지난 글에서는 연결리스트가 사용하는 메모리 공간을 어떻게 관리하는지 그 구현을 C언어로 직접 해보았다.
이번 글에서는 트리와 이진트리의 개념을 정리해보고자 한다.
트리
트리는 아래와 같이 정의된다.
a tree is a finite set T of nodes such that
1) T has one special node called root
2) the remaining nodes are partitioned into m disjoint sets T1, T2, ... Tm, and each of these sets is turn to a tree.
wee call them subtrees of T
트리는 '루트' 라고 불리는 특별한 하나의 노드를 가지고 있고, 나머지 노드들은 m 개의 서브트리를 이루는 유한한 노드 집합이라고 한다.
(간단히 말하면 서브 트리들을 모아서 루트로 묶은 걸 트리라고 한다. 재귀적 정의)
내가 알던 트리의 정의는 그래프 중 사이클이 없고, 모든 노드에 대해 한 노드로부터 다른 노드까지 이동 경로가 유일하게 존재하는 그래프를 트리라고 했던 것 같긴한데, 아직 '그래프' 라는 자료구조를 설명하지 않은 상황이라 이렇게 정의된 것 같다.
트리에서 사용하는 용어
root : 루트 노드, 트리의 중심 / 시작점이다.
degree : 한 노드에서 아래로 뻗어나온 edge 개수 (자신과 부모 노드의 edge 는 아니다)
leaf : degree = 0 인 노드. terminal node 라고도 한다. leaf 노드가 아닌 노드는 nonterminal node 또는 internal node 라고 한다.
depth (level) : root 노드의 depth 를 0 이라고 하고, i-depth 의 child node 는 (i+1)-depth 를가진다.
height : max of depth
이진 트리 (Binary Tree)
이진 트리는 아래와 같이 정의된다.
A binary tree is a finite set of nodes that either is empty or, (if not empty) consists of a root and two disjoint binary trees that are called the left subtree and the right subtree.
역시 재귀적 정의이다.
이진 트리는
1) 비어있는 공집합 트리거나 (이것이 트리와의 차이점이다. 트리는 루트가 반드시 존재해야 한다.)
2) 분리된 left subtree, right subtree 와 root 로 구성된 트리이다.
이진트리는 공집합 트리가 아니라면 반드시 left, right subtree 를 가진다. (degree 가 2 이다.)
(공집합도 이진 트리 이므로, left / right subtree 가 공집합이어도 된다.)
이진트리를 그릴 때는 반드시 좌/우를 구분해야 하기 때문에, 좌 / 우 중 한쪽이 비어있더라도 그냥 일직선으로 그리면 안된다. (공집합이 있음을 기억하자.)
그래서 헷갈리지 않게, 공집합도 다른 기호를 통해 표시하여 이진 트리를 그리기도 한다.
이를 Extended Binary Tree 라고 부른다.
이를 그림으로 표현해보면 아래와 같다.

이진트리를 그릴 때는 반드시 좌/우를 구분해서 그려야 한다고 했다.
따라서 아래와 같은 이진트리는 서로 다른 이진트리이다.

이것으로부터 재밌는 개념이 하나 생겨나는데, 바로 '카탈란 수' 이다.
Enumeration of Binary Trees (서로 다른 이진 트리 개수)
Tn 을 n개의 노드를 갖는 서로 다른 이진트리의 개수라고 해보자.
T0 = 1 (공집합)
T1 = 1 (노드가 1개)
임은 간단하게 알 수 있다.
T2 = 2 임은 위 그림에서 보듯 알 수 있다.
T1 경우의 수에서 왼쪽에 붙이거나 오른쪽에 붙이거나 하면 2가지 경우가 나온다.
이를 일반화하면, N > 1 일 때, 루트 노드를 제외한 나머지 노드는 왼쪽 또는 오른쪽 서브트리에 속해있다.
만약 왼쪽 서브트리에 l 개가 있다면 오른쪽 서브트리에는 n - l - 1 개가 있을 것이다. (루트노드는 제외하므로)
이를 r 이라고 하면 r = n - l - 1 에서 r + l = n - 1 이다.
l, r 이 정해진 상황에 이에 대한 경우의 수는 Tr * Tl 이고,
l, r 은 0 <= l <= n-1 , r = n - l - 1 범위에서 나타나므로 이를 모두 더하면 Tn 의 경우의 수를 계산하는 점화식이 아래와 같이 나온다.
Tn = t0 * tn-1 + t1 * tn-2 + ... tn-1 * t0
T0 = 1, T1 = 1 이라는 초기 값을 알고 있기 때문에, 임의 Tn 을 계산할 수 있으며, 이 Tn 을 카탈란 수 라고 부른다.
카탈란 수 Cn = 2nCn / (n+1)
여기에 더해 기출문제에 나왔던 Cn <= n! 을 증명해보자.
수학적 귀납법을 이용하면 증명할 수 있다.
우선 n = 1 일 때, C1 = 2C1 / 2 = 1 <= 1 이므로 성립한다.
n = k 일 때, 2kCk / (k + 1) <= k! 이 성립한다고 가정해보자.
이 때 n = k+1 일 때, 2(k+1)C(k+1) / (k+2) <= (k+1)! = (k+1) * k! 이 성립하면
수학적 귀납법에 의해 Cn <= n! 이 증명된다.
양변을 (k+1) 로 나누면, 2(k+1)C(k+1) / (k+1)(k+2) <= k!
이때 n = k 일 때 2kCk / (k+1) 이 항상 k! 이하이므로
만약 2(k+1)C(k+1) / (k+1)(k+2) <= 2kCk / (k+1) 라면,
2(k+1)C(k+1) / (k+1)(k+2) <= 2(k+1)C(k+1) / (k+1)(k+2) <= k! 에서 성립한다.
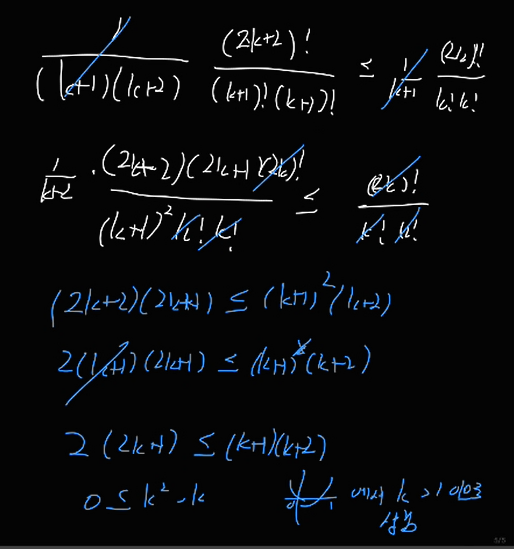
따라서 카탈란 수는 n! 이하이다.
지금까지 트리와 이진트리에 대해 정리하였다.
다음 글에서는 이진트리를 순회하는 3가지 방법에 대해 정리해보고자 한다.
'CS > 자료구조' 카테고리의 다른 글
| [자료구조 및 프로그래밍] 9. 이진 탐색 트리 (3) | 2023.10.22 |
|---|---|
| [자료구조 및 프로그래밍] 8. 이진 트리의 순회 (0) | 2023.10.22 |
| [자료구조 및 프로그래밍] 6. 메모리 관리 시스템 (0) | 2023.10.18 |
| [자료구조 및 프로그래밍] 5. Stack & Queue With Linked List (0) | 2023.10.17 |
| [자료구조 및 프로그래밍] 4. Linked List (0) | 2023.10.12 |
