투상 (Projection)
3D 물체를 2D 평면에 사상하는 것을 말한다.
지난 글까지 각종 행렬 변환을 통해 ' Model 좌표계 → World 좌표계 → View 좌표계 ' 까지 변환했다면
이렇게 변환된 좌표계 위에 놓인 3D 물체를 2차원 화면에 사상하는 과정이다.

먼저 용어부터 정리하자.
1. 투상면, View Plane = Projection Plane
화면에 그리기 전 최종 변환된 좌표계 위 3D 물체를 투상하는 2D 화면을 의미한다.
물체 영상이 이 곳에 맺힌다.
2. 관찰자 위치, View Point, Eye Position, Camera Position
투상의 기준은 관찰자의 위치로부터 결정된다.
이 위치를 '시점 좌표' 라고 한다.
3. 투상 중심 (COP = Center Of Projection)
투상면의 중심을 말한다.
View 좌표계의 원점과 같다.
4. 투상선 (Projectors)
투상 중심과 물체를 연결한 선을 말한다.
이 선이 투상면과 만나는 위치에 정점이 투상된다.
5. 시선 (Line of Sight)
관찰자(카메라)가 바라보는 방향이다.
설정 방법에 따라 전역좌표계의 원점을 향하기도 하고, 임의 위치의 초점을 향하기도 한다.
평행 투상 (Parallel Projection)

시점이 물체로부터 무한대의 거리에 있다고 간주하여, 투상선을 나란히 가져가는 투상법이다.
즉, 원근감을 부여하지 않는다.
평행 투상은 또 '정사 투상', '축측 투상', '경사 투상' 으로 구분된다.
정사 투상 (Orthographic Projection)
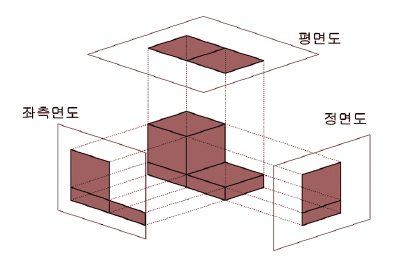
평면도 (top / bottom view)
입면도 (front / rear view)
측면도 (left / right view)
이렇게 3가지를 말한다.
모델 좌표계의 주축(Principal Axes) 인 x, y, z 축에 의해 형성되는 평면 (xy, yz, zx 평면) 을 주 평면(Principal Plane) 이라고 할 때, 정사 투상의 투상면은 주 평면 중 하나에 놓인다.
정사 투상에서 투상선은 투상면에 직교해야 한다. 따라서 시점의 위치가 제한된다.
투상된 상이 원래 물체의 길이를 그대로 보존하기 때문에, 정확성을 요구하는 공학 도면에 주로 사용한다.
OpenGL 에서 평행 투상 사용하기

glm::ortho() 함수를 사용하면 평행 투상을 적용할 수 있다.
투상은 가시부피 (View Volume) 안에 있는 것만 투상한다.
위 그림 기준으로 보면 녹색 정육면체는 투상되지만, 파란색 정육면체는 투상되지 않는다.
파라미터로 가시부피의 좌, 우, 하, 상, 앞, 뒤 값을 넘긴다.
이때 앞, 뒤 값에 해당하는 near, far 데이터는 반드시 '양수' 를 넘겨야 한다. (왼손 좌표계)
다만 실제 z좌표는 -1 을 곱해야 한다.
예를 들어 위 이미지의 near plane 의 오른쪽 상단 점의 실제 좌표는 (right, top, -near) 가 된다.
원근 투상 (Perspective Projection)
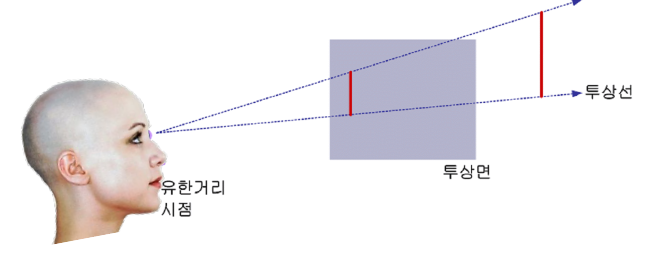
시점이 물체로부터 유한한 거리만큼 떨어져있다고 간주하고, 모든 투상선이 시점에서 출발해서 방사선 모양으로 퍼저간다고 보는 방법이다.
사람과 카메라 렌즈가 실제로 물체를 인식하는 방법이다.
이 관점을 사용하면 크기가 동일한 물체라고 하더라도, 먼 곳에 있는 물체는 투상면에 작게 투상되고,
가까운 곳에 있는 물체는 투상면에 크게 투상된다.
이로 인해 물체의 원근감 (Depth Feeling) 이 나타난다.
소실점 (VP : Vanishing Point)

원근투상을 하는 경우, 실제로는 평행한 선이 한 점에서 만나는 듯 보이게 된다.
소실점은 시점 높이에서 평행선이 만나는 점을 가리킨다.

소실점 수에 따라서 원근 투상을 일점 투상 (One-point Projection), 이점 투상 (Two-point Projection), 삼점 투상 (Three-point Projection) 등으로 나누기도 한다.
OpenGL 에서는 기본적으로 일점 투상을 가정한다.
OpenGL에서 원근 투상 사용하기
glm::perspective() 함수를 사용하면 된다.
원근 투상도 평행 투상과 마찬가지로 가시부피에 있는 것만 투상한다.
그런데 가시부피를 구하는 방식이 평행 투상과 조금 다르다.

평행 투상은 멀리있는 것과 가까이 있는 것, 투상면의 크기가 모두 동일했다.
하지만 원근 투상은 멀리 있는 투상면과 가까이 있는 투상면의 크기가 다르다.
그림에서 보는 것처럼 멀리 있는 가시부피의 후방절단면이 전방 절단면보다 더 크다.
실제 투상면은 이보다 더 앞에 있을 수 있으며, 크기가 더 작아진다.
이렇게 원근 투상의 가시부피는 절단 사각뿔 (Frustum)의 형태를 갖는다.

이를 실제 화면에 보여줄 때는 위와 같이 투상면에 맞춘 변환과정을 거친다.
전방 절단면의 크기를 키우고, 후방 절단면의 크기를 줄여서 정육면체 모양으로 바꾸는 것이다.
그러면 자연스럽게 전방 절단면에 위치한 물체는 크기가 커지고, 후방 절단면에 위치한 물체는 크기가 작아진다.
즉, 가까이 있는 물체는 크게 보이고, 멀리 있는 물체는 작게 보이도록 구현된다.
이런 변환 과정을 가리켜 Perspective Normalization 이라고 한다.
구체적인 변환 과정을 따라가보자.
Perspective Normalization

1. (a) → (b)
(a) 의 가시부피를 z축 기준으로 대칭이 되도록 (b) 형태로 바꿔준다.
이를 위해 전단(shearing) 변환을 거친다.

전단 변환은 위와 같은 행렬식을 사용하면 된다.
(a) 에서 보라색 점은 절단면의 중앙에 위치한다. 그 좌표를 ( (r+l) / 2, (t+b)/2, -n, 1) 이라고 하자.
r = rigt, l = left, t = top, b = bottom, n = near
n 은 전방 절단면의 왼손 좌표계 z 좌표이다. (즉, 전방 절단면과 시점 사이 거리)
따라서 실제 좌표로는 -n 이 곱해진다.
위 행렬에 보라색 점의 좌표를 넣어서 곱하면 아래와 같이 계산된다.
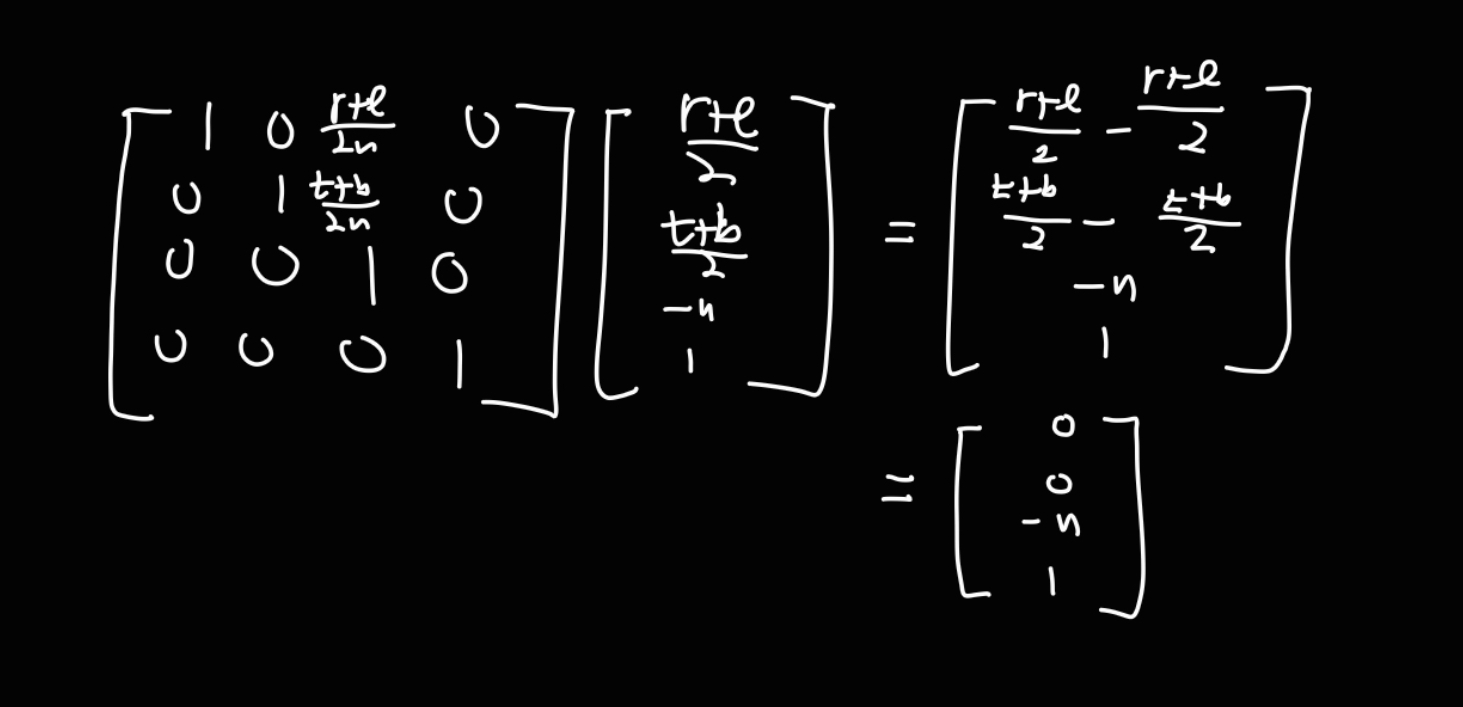
따라서 투상면의 중점 x, y 좌표가 모두 0 으로 맞춰진다.
원근 투상에서 투상면과 전후방 절단면은 시선(시점으로부터 초점을 연결한 선)에 수직으로 놓여있다.
하지만 위와 같이 시선과 절단면이 서로 수직이 아닐 때, 이를 수직으로 맞춰주는 작업이 필요하다.
2. (b) → (c)

다음은 전방 절단면의 가로, 세로 길이를 2n 으로 맞춰준다.
이 작업을 하는 이유는, 전방절단멸의 시점으로부터의 거리인 n을 절단면 크기에 반영하기 위함이다.
n이 크다면 전방 절단면의 실제 크기도 더 커질 것이다.
(멀리 떨어져 있으면, 더 많은 것들을 담을 수 있다.)
이 변환을 하기 위한 행렬을 한번 (a) 기준에서부터 차례대로 적용해보자.
우선 절단면 중점은 크기 변환에 영향을 받지 않으므로, 오른쪽 위 모서리에 대해 (a) - (b) 변환을 거쳐주자.

그림과 같이 변환된다.
이제 이 좌표를 (n, n, -n, 1) 로 바꿔주면 된다.
그러려면 2n / (r-l) 을 x에 곱해주고, 2n / (t-b) 를 y 에 곱해주면 될 것 같다.
따라서 변환행렬이 아래와 같이 나온다.
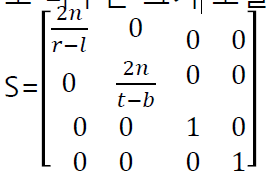
3. (c) → (d)
이제 n, f 에 대해 변환해주면 된다.
최종적으로 만들고자하는 가시부피는 전방 절단면의 z 좌표(-n)가 -1, 후방 절단면의 z좌표(-f) 가 1 이 되어야 한다.
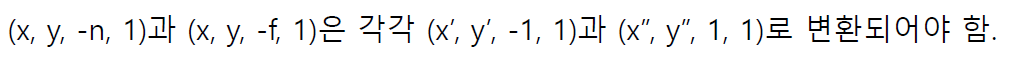
따라서 이렇게 변환되도록 전방절단면에는 z에 n을 나눠주고, 후방 절단면에는 -f 를 나눠준 결과물이 적용되도록 아래와 같이 행렬을 쓸 수 있다.

이 행렬을 이용해 연산하면 (x, y, -n, 1) 이 (x, y, -n, n) 으로 나온다.
동차 좌표계에서 (x, y, z, w) 로 표현된 점은 실제 3차원 좌표계에서는 (x/w, y/w, z/w) 로 표현되기 때문에 이를 (x', y', -1) 로 표현한 것으로 볼 수 있다.
따라서 이 행렬을 적용하면, z 좌표가 -1 ~ 1 사이로만 나오게 된다.
4. 종합
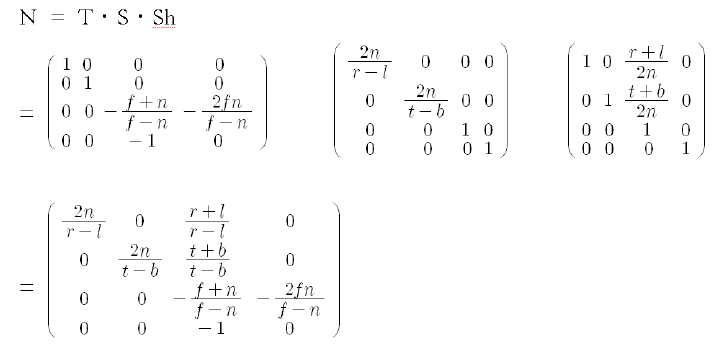
이 과정을 종합하면 위와 같은 변환 행렬을 얻을 수 있다.
그렇다면 OpenGL 에서 glm::perspective() 함수로 원근 투상을 할 때, r, l, t, b, n, f 값을 모두 넘겨야 할까?
사실 그렇지 않다.
필요한 값은 FOV, Ratio, n, f 4가지 값이면 충분하다.
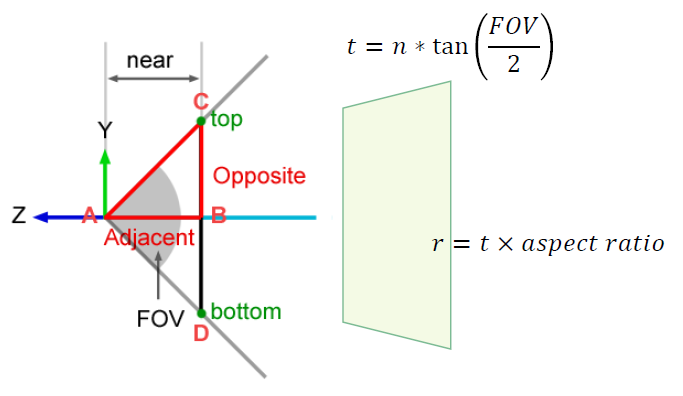
아래 그림을 보면 그 이유를 알 수 있다.
FOV (Field Of View) 는 가시각을 의미한다.
이 가시각과 near 평면 (전방 절단면) 사이 거리를 이용하면, 세로 길이 t 값을 구할 수 있다.
그리고 t 값이 구해지면, 화면 비율 ratio 값에 t를 곱해서 가로 길이 r도 구할 수 있다.
l, b 값은 필요하지 않다.
그 이유는 원근 투상을 할 때 시선은 절단면과 투상면에 반드시 수직해야 하는데, z 축을 시선으로서 수직으로 꽂으면 l, b 값은 r, t 값과 대칭이 되기 때문이다.

따라서 원근투상의 가시 부피를 나타낼 때는 fov 와 aspect, near, far 값만 있으면 되고, 이 순서대로 glm::perspective() 함수에 넘겨주면 원근 투상으로 알아서 변환해준다.
시야각 fov 는 0~180 사이의 값을 가진다.
aspect 가 뷰 종횡비 (aspect ratio, 가로 / 세로) 를 나타낸다.
그리고 평행 투상과 마찬가지로 near, far 값은 항상 양수여야 한다.
'CS > HCI 윈도우즈프로그래밍' 카테고리의 다른 글
| 중간고사 최종 정리 (1) | 2024.04.22 |
|---|---|
| [OpenGL] 18. Transformation (6) - View Change (VCS) (0) | 2024.04.21 |
| [OpenGL] 16. Transformation (4) - 셰이더에 행렬 변환 적용하기 (1) | 2024.04.19 |
| [OpenGL] 15. Transformation (3) - GLM 사용하기 (0) | 2024.04.19 |
| [OpenGL] 14. Transformation (2) - 복합 변환 (0) | 2024.04.18 |
