Homography
homography는 평면 투영 변환 행렬을 가리키는 말이다.
평면 투영 변환은 2차원 평면에 어떤 변환 H를 가해 다시 2차원 평면으로 만드는 것을 말한다.
이걸 사용하는 이유는 수학적으로 어려운 개념을 인간의 관점에서 쉽게 이해하기 위함이다.
예를 들어 이전 내용에서 무한대에 위치한 점은 homogeneous 좌표계로 나타냈을 때 세번째 원소가 0이었고, 이들을 모두 이으면 하나의 원이 나온다고 했었다.
그런데 이런 수학적인 표현은 인간의 두뇌로는 상상도 잘 안되고 이해하기 힘들다.
그래서 그냥 평행선이 있다고 할 때 이걸 인간의 시점에서 잘 비틀어보는 것이다.
그러면 우리가 도로를 바라볼 때 먼 지점의 도로가 한 점에서 만나듯 (소실점) 무한대에 있는 점들은 한 곳에서 만난다는 것을 인간의 시점에서 보면 이해할 수 있다.
특히, 2차원 장면 (scene)을 이리 저리 틀어보면서 3차원 복원을 한다거나 할 때 (SLAM) 많이 쓰인다.
2차원 평면을 2차원 평면으로 변환할 때, homogeneous를 사용하게 되면 3 x 3 행렬을 사용하게 된다.
이때, 이 행렬은 non-singular 해야 하는데, 이 말은 이 행렬이 반드시 역행렬이 존재해야 한다는 것과 같다.
또 이 행렬의 결과로 나온 3차원 벡터도, homogeneous하게 표현되어 있다. 따라서 어떤 스칼라를 변환 행렬에 곱해도 변환하는 내용, 과정은 동일하다.

이제 Homography를 H 라고 할 때, 점을 변환하는 경우는 위와 같이 쓸 수 있다.
그렇다면 선, conic을 변환할 때는 어떻게 할 수 있을까?
먼저, 선을 변환하는 경우를 생각해보자.
homography를 사용하여 선을 변환하는 경우, 항상 직선은 직선으로 변환된다.
어떤 직선 l을 구성하는 임의의 세 점 x1, x2, x3 이 있다고 하자.
그러면 다음이 성립함을 알 수 있다.

이때, 변환된 직선 l` 위의 점 x`을 다음과 같이 생각해보자.

어쨌든 직선을 변환할 때 H에 기반하여 변환했다면, 직선을 구성하는 각각의 점들에 대해 위와 같은 식을 적용한 점의 집합을 l` 이라고 볼 수 있을 것이다.
이때 이 식을 xi 에 대해 다음과 같이 바꿔 쓸 수 있다.
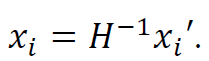
이제 이 식을 위에서 쓴 직선 식에 대입해보자.
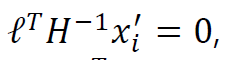
그러면 다음과 같이 식이 나온다.
이를 통해 어떤 직선에 대해 H 라는 homography를 적용한 직선은

이렇게 나타낼 수 있다는 것을 알 수 있다.
이번엔 conic을 어떻게 변환할 수 있는지 생각해보자.
conic을 나타내는 행렬 C 에 대해

다음 등식이 성립하는 것을 알고 있다.
마찬가지로 이 x에 직선에 대입했던 것처럼 그대로 대입하면
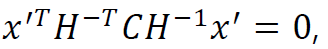
위와 같은 식을 얻을 수 있다.
따라서 변환된 conic 행렬 C` 은

와 같다는 것을 알 수 있다.
이를 이용해서 conic을 변환하면

위 이미지와 같이 변환되는 과정을 볼 수 있으며, 사람의 눈을 모방한 실제 카메라에서도 사이드로 가면 물체가 늘어져보이는 왜곡이 발생하는 것과 같은 왜곡을 표현할 수 있다.
'CS > HCI 윈도우즈프로그래밍' 카테고리의 다른 글
| [Computer Vision] 5. Edge Detection (0) | 2024.06.07 |
|---|---|
| [Computer Vision] 4. Geometry Primer (3) : Transform (0) | 2024.06.02 |
| [Computer Vision] 2. Geometry Primer (1) : Homogeneous Coordinates (3) | 2024.05.31 |
| [Computer Vision] 1. introduction (0) | 2024.05.29 |
| 중간고사 최종 정리 (1) | 2024.04.22 |
