Group
모든 평면 투영 변환의 집합들은 그룹을 형성한다.
그리고 각각의 그룹에는 특별한 케이스들이 있다.
이제 다양한 특별한 케이스 (특별한 평면 투영 변환) 을 정리한다.
우선 group은 아래와 같은 특성을 갖는다.
1. 특정 그룹에 속하는 a, b 에 대해서, a와 b를 연산현 결과도 그 그룹 안에 속한다.
이를 '닫혀있다' 라고 표현한다.
2. 연산 순서에 영향을 받지 않아야 한다. (associative 하다고 한다.)
3. identity element를 가져야 한다.
identity element는 이 element와 다른 element를 연산했을 때, 그 다른 element가 그대로 나오도록 하는 element를 말한다.
4. 특정 group 안에 있는 모든 element에 대해, 그들의 inverse 역시 그 group 안에 있어야 한다.
inverse는 element와 연산한 결과가 identity element가 나오도록 하는 element를 말한다.
GL(3) & PL(3)
3 x 3 크기의 non-singular 행렬의 곱셈은 이 4가지를 모두 만족한다.
이 그룹을 GL(3) 이라고 하자. (GL은 General Linear 라는 뜻)
이 GL(3) 이라는 그룹 내에 있는 모든 행렬은 homography로 쓸 수 있다.
그런데 어떤 행렬에 스칼라를 곱한 행렬은 homography 관점에서는 모두 동일한 homography이다.
따라서 서로 다른 homography를 구분하려면 GL(3) 안에서도 다른 구분 기준으로 나누어야 한다.
이렇게 임의의 스칼라끼리 같은 homoraphy를 구성하는 것을 고려하여 나눈 group을 PL(3) 이라고 한다.
(Projective Linear)
이때 이 PL(3) 안에서 특징에 따라 아래와 같은 계층으로 sub group을 분류할 수 있다.
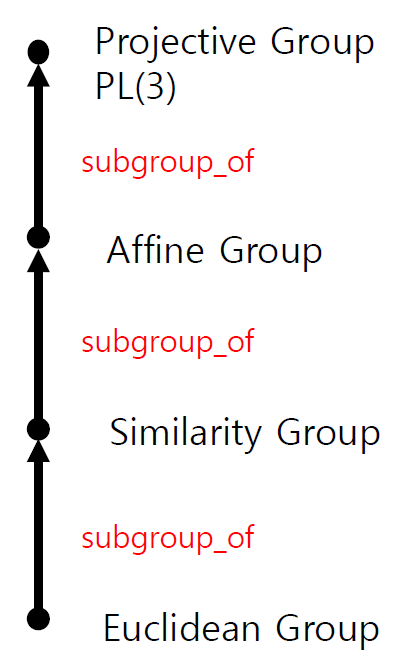
이를 통해 알 수 있는 점은
Affine Group 과 Affine Group을 연산하면, Affine Group에 속한 행렬이 나온다.
Affine Group 과 Similarity Group을 연산하면, Affine Group에 속한 행렬이 나온다.
(Similarity Group은 Affine Group의 서브 그룹이기 때문)
PL(3)을 나타낼 때, 그냥 3x3 행렬로 나타내기보다 아래와 같은 방식으로 나타내보자.
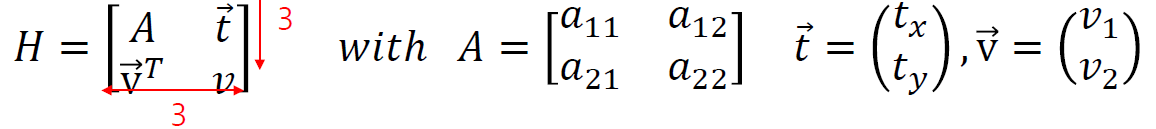
이때 H 는 homogeneous이므로, 비율이 중요하다.
따라서 v는 항상 1이 되도록 맞춘다고 하자.
뒤에서 v = 0 이 되는 케이스도 다룰 것이다.
이제 Affine Group, Similarity Group, Eucliean Group 에 대해 정리해보자.
Affine Transformation
한글로는 아핀 변환이라고 한다.
아핀 변환은 일반적인 PL(3) 에서 마지막 3번째 행의 값이 (0 0 1) 인 행렬이다.

그래서 두 Affine 변환을 곱하면 그 결과는 항상 Affine 변환 행렬이다.
이때 A 는 non-singular 이다. 즉 det(A) 가 0 이 아니므로 역행렬이 항상 존재한다.

아핀 변환은 실제로 이렇게 쓸 수 있다.
x1, x2 는 물리적으로는 평면을 나타내는 점이 된다.
아핀 변환이 평면을 어떻게 변환시키는지 보기 위해, tx, ty 에 모두 0을 넣어보자.

그러면 이렇게 변환식을 쓸 수 있게 된다.
이를 그림으로 나타내면

이렇게 나타낼 수 있다.
아핀변환은 직선을 직선으로 유지시킬 뿐만 아니라, 평행한 직선은 그대로 평행을 유지하도록 변환시킨다.
이는 아핀 변환에 무한대 점을 넣어보면 알 수 있다.
무한대 점은 두 평행선의 교점이므로, 무한대 점을 변환했을 때 항상 무한대가 나온다면, 두 평행선을 아핀변환에 넣으면 항상 평행이 유지된다고 생각할 수 있다.
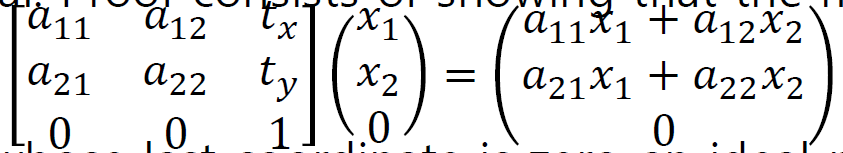
이렇게 임의의 무한대 점을 넣으면 항상 마지막 원소가 0인 무한대 점이 나오는 것을 알 수 있다.
Similarity Transform
similarity transform은 형태가 유지되는 변환이다.
이 group은 affine group에 추가적으로 A 가 orthogonal 하다는 조건을 더한 것과 같다.
그러면 아래가 성립한다.
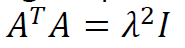
이 변환의 기하학적 특징으로는, 두 직선 사이의 각이 보존되는 것이 있다.
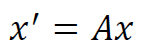
어떤 변환의 결과로 나온 점 x' 을 위와 같이 표현할 때,

어떤 점 x의 놈(크기)을 위와 같이 표현할 수 있다.
이때 A전치와 A의 곱은 추가된 조건에 따라 람다 제곱 I 로 나타난다.

람다는 상수이므로, 이를 앞으로 빼내면 위와 같은 식이 성립하므로, x의 놈에 람다를 제곱한 것과 같다.
이제 이 사실을 기억해두고, 한 평면 위에 있는 서로 다른 두점 x, y 를 생각해보자.
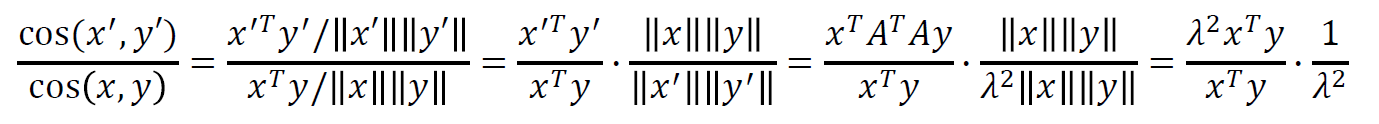
이때 x, y 사이의 각도와 x' y' 사이의 각도를 구해보면 위와 같이 식을 전개할 수 있다.
이 식의 최종 값은 1 이므로, 두 각도가 같음을 알 수 있다.
결론은 similarity transform 은 각도가 보존되는 변환이다.
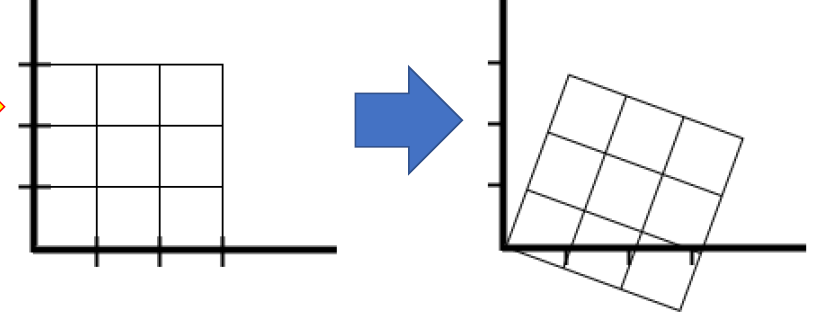
이를 그림으로 나타내면 위와 같다.
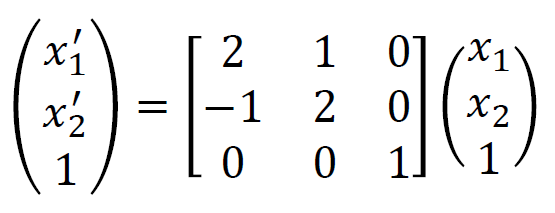
행렬로는 위와 같이 나타낼 수 있다.
Euclidean Transfromation
유클라드 변환에 의한 유클라드 group은 similarity 변환에 추가적으로 orthonormal 이라는 조건을 더한 것과 같다.
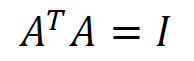
그러면 위와 같은 식이 성립하면서 A의 전치와 A의 역행렬이 같아진다.
이 변환은 변환 결과 임의의 두 점 사이 거리가, 변환 전과 똑같이 보존된다는 특징을 가진다.

증명은 위 수식으로 할 수 있다.
d(x', y') 은 변환된 두 점 사이의 거리를 나타낸다. 이 식 중간에 A전치와 A의 곱이 identity 를 나타내는 점을 이용하여 추가한 뒤 정리하면 d(x, y) 가 나오는 것을 볼 수 있다.
Projective 변환에 의해 생성된 왜곡의 특징
카메라로 넓은 범위의 사진을 찍을 때 발생하는 왜곡이 있다.
이 왜곡은 다음과 같은 특징을 갖는다.
homography H 가 무한대의 점으로 구성된 선 (소실선) 을 무한대의 점으로 구성된 선으로 변환한다면,
그 H는 affine 변환이다.
이때 무한대의 점으로 구성된 선은 (0, 0, 1) 의 성분을 가진다는 것을 기억하자.
어떤 직선을 변환할 때는 H의 역행렬의 전치가 필요하다.

이를 위와 같이 정의하자.
(A는 역행렬이 존재하는 2x2 행렬이다.)

이때 H의 역행렬은 위와 같이 나타낼 수 있다.
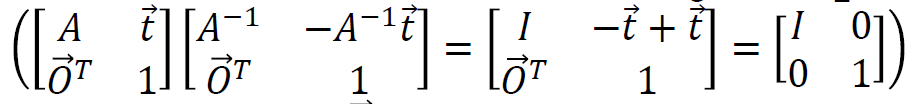
이렇게 둘을 곱해보면 identity 행렬이 나오는 것을 확인할 수 있으므로, 역행렬이 맞다.
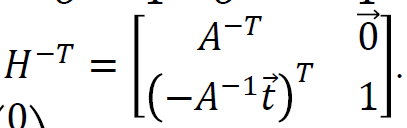
따라서 H의 전치의 역행렬은 위와 같이 나타낼 수 있으며, 무한대의 점을 이 행렬에 곱해보면
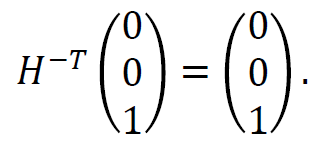
이렇게 항상 나온다는 것을 알 수 있다.
그리고 이게 되려면 아핀 변환의 특징인 3행이 (0 0 1) 이 되어야 한다.
만약 0 0 1 이 아니라면

x축 위의 무한대 점에 대해 변환을 가하면

다음과 같이 나올 것이다.
이 변환의 결과가 무한대가 되려면 v1 = 0 이 되어야 한다.
마찬가지로 y축 위의 무한대 점에 대해 계산하면 v2 역시 0이 되어야 함을 알 수 있다.
따라서 아핀 변환은 무한대 직선을 무한대로 변환한다.
반면 일반적인 투영 변환은 무한대 직선을 어떤 직선으로 변환하게 되는데, 이 직선을 소실선 (vanishing line) 이라고 한다.

이를 그림으로 보면 위와 같다.
아핀 변환은 평행선을 평행하게 유지시키므로, 무한대 직선을 그대로 무한대로 유지시킨다.
(무한대 위치에 있는 점들이 여전히 무한대에 위치한다.)
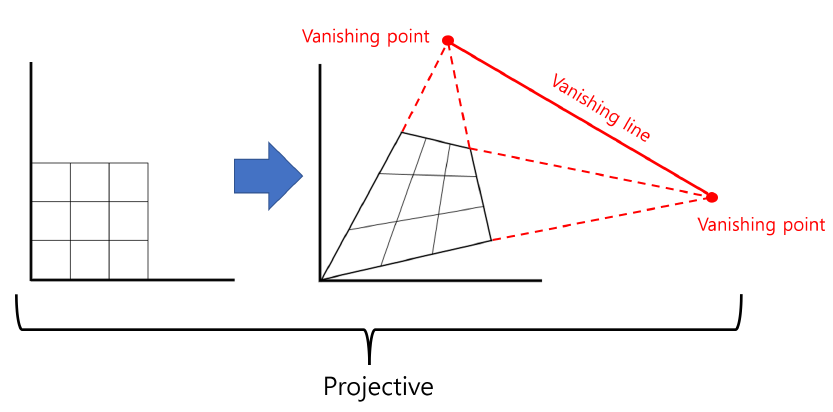
반면 일반적인 투영 변환은 무한대에 존재해야 하는 점들이 한 점에서 모이게 되는데, 이 각각의 무한대 점들을 이으면 하나의 선이 된다.
이 선을 소실선이라고 한다.
만약 이렇게 소실선이 존재하는 이미지에 대해 어떤 homography를 적용해서 소실선이 무한대 점들로 구성된 선이 되게 한다면, 이미지에 남아있는 왜곡이 affine 변환에 의한 왜곡만 남고 나머지는 사라지게 될 것이다.
재미있는 것은, 이 왜곡을 없애는 방법이 소실선을 구성하는 3개의 파라미터에 의해 구해진다는 것이다.
만약 어떤 소실선을 아래와 같이 나타내는 경우,
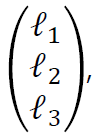
아래와 같은 변환을 사용하면 소실선을 무한대 점들로 구성된 직선으로 만들 수 있다.

이를 증명하기 위해 먼저 H의 역행렬을 구해보면
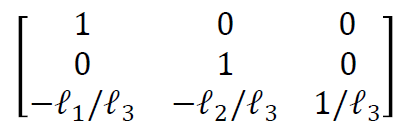
다음과 같이 나오고, 다시 이에 대해 전치를 거치면

위와 같이 나온다.

이제 이 행렬에 기존의 소실선을 넣으면, 그 소실선이 변환되기 이전의 직선이 나오는데, 이 직선은 (0 0 1) 로 무한대 직선이 나오게 된다.
한번 연습으로 소실선을 구해보자.

이 이미지에서 소실선 식을 어떻게 구할 수 있을까?
1. l1, l2 식을 구해서 이 둘의 교점을 구한다. (이 교점은 Q 점으로 나타나는데, 사실 이 점은 무한대 점이다.)
2. l3, l4 식을 구해서 이 둘의 교점을 구한다. (이 교점은 P 점으로 나타나는데, 사실 이 점은 무한대 점이다.)
3. P, Q 를 외적하면 소실선이 나온다.

먼저 l1, l2, l3, l4는 위와 같이 두 점의 외적으로 구할 수 있다.

두 점 P, Q 는 위와 같이 구할 수 있다.
마지막으로 소실선은

위와 같이 구할 수 있다.
소실선을 구했으므로, 이제 소실선을 무한대 선으로 만드는, 왜곡을 아핀만 남게 하는 행렬을 만들 수 있다.
'CS > HCI 윈도우즈프로그래밍' 카테고리의 다른 글
| [Computer Vision] 6. Feature Detection (4) | 2024.06.09 |
|---|---|
| [Computer Vision] 5. Edge Detection (0) | 2024.06.07 |
| [Computer Vision] 3. Geometry Primer (2) : Homography (0) | 2024.05.31 |
| [Computer Vision] 2. Geometry Primer (1) : Homogeneous Coordinates (3) | 2024.05.31 |
| [Computer Vision] 1. introduction (0) | 2024.05.29 |
