Edge Detection의 기본 원리
어떤 물체의 내부, 또는 그 물체의 배경에 대해 변화가 작다면, 배경과 물체 사이의 경계 주위에서는 큰 변화가 있을 것이다.
이 관찰에 기반해서, Edge detection 알고리즘은 밝기, 색상, 텍스쳐 등의 변화량을 측정하고, 큰 변화가 발생한 위치를 edge로 인식한다.
이 작업을 수행하기 위한 가장 간단한 방법은, 각 픽셀에서 gray level의 gradient vector를 계산하는 것이다.
이미지를 흑백으로 바꾼 뒤, 밝기의 차이만 보는 것이다.

그 값은 위와 같이 계산할 수 있다.
또한 절대적인 변화량은
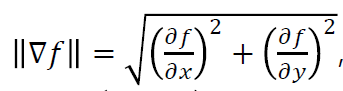
이렇게 절댓값을 씌워서 얻을 수 있다.
그리고 이 변화량은 마치 수학에서 두 점 사이의 변화량을 보는 것과 같이 그 변화의 뱡향을 따질 수 있다.
이때 변화의 방향 각도를 아래와 같이 구할 수 있다.

이제 이 f에 대해 1차원에서 도함수를 구하면

이렇게 도함수를 구할 수 있다.
그러면 변화가 가장 큰 각도를 구할 수 있다.
그런데 우리가 보는 이미지는 디지털이미지로, 픽셀의 위치가 뚝뚝 끊어져 있기 때문에, 이 도함수는 적절히 추상화해서 연속인 것처럼 나타내야 한다.
두 픽셀 사이의 간격의 최소값은 1이기 때문에
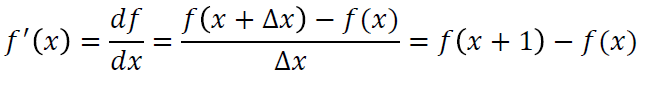
도함수를 위와 같이 나타낼 수 있다.
그리고 이 표현을 다음과 같이 나타내기도 한다.

현재 x 위치에는 -1을 곱하고, x+1 위치에는 1을 곱한 뒤 더한 값을 현재 x의 값으로 취한다는 뜻이다.

이를 위와 같은 1차원 디지털 이미지에 적용하면
0 위치의 f' 값은 f(x+1) - f(x) 에서 f(1) - f(0) = 2 - 2 = 0 이다.
1 위치의 f' 값은 f(2) - f(1) = 3 - 2 = 1 이다.
이런식으로 칸을 채우면 아래와 같이 도함수 칸을 채울 수 있다.

이때 이 값을 binary 값으로 바꿀 수 있다.
그 기준으로 사용하는 것이 threshold (임계값) 이라고 하는데, 이 값보다 절댓값이 크거나 같으면 1로, 작으면 0으로 설정할 수 있다.

그러면 위와 같이 나타낼 수 있다.
여기에 더해서 이계도함수를 생각해볼 수도 있다.
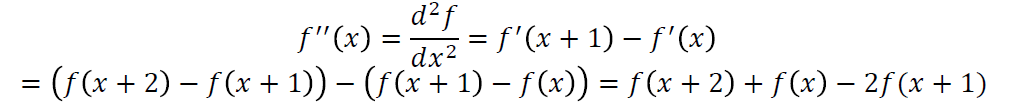
이계도함수는 위와 같이 구할 수 있다.
이 최종 결과를 아까와 같이 표(마스크)로 표현하면 아래와 같이 표현된다.

이를 적용한 예제로서 아래를 보자.

위 이미지에서 선은 기존 디지털 이미지의 밝기 그래프를 나타낸다.
밝기가 3과 4 사이에서 한번 크게 변하고 이후로는 작게 변환다.
f'은 f(x+1) - f(x) 를 사용한 것, f'' 은 f(x+2) + f(x) - 2f(x+1)를 적용한 것이다.
변화량을 보면 인덱스 3에서 '4' 라는 변화량으로 크게 나타났다가 그 뒤로는 -1 씩 오랫동안 감소한다.
이에 대해 이계도함수를 구하면 4 -> -4 로 값이 크게 변하는 포인트가 존재한다.
이렇게 부호가 변하는 부분은 0을 지나간다고 해서 '제로 크로싱' 이라고 한다.
이렇게 제로 크로싱이 발생하는 부분을 엣지 경게로 파악한다.
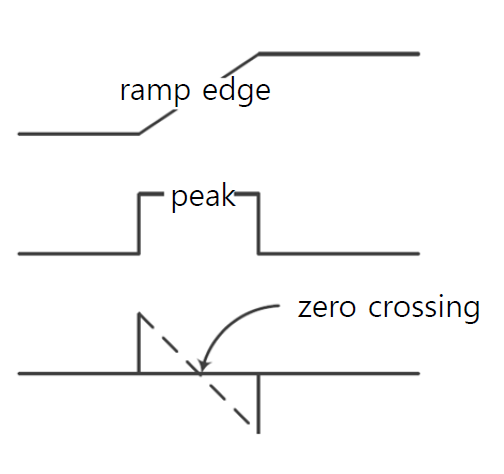
그런데 이런 방식을 사용하는 경우에 한가지 문제점은, 위 그림의 ramp edge 처럼 천천히 변하는 경우 검출하기가 힘들어진다. 매우 급격하게 변화하는 값만 알 수가 있는 방식인 것이다.
Sobel and Scharr Operators
이 문제를 해결하기 위해 새로운 방법이 등장하였다.
Sobel은 아래와 같은 3x3 마스크를 대신 사용한다.

왼쪽 행렬은 x축에 대해, 오른쪽 행렬은 y축에 대해 사용하는 행렬이다.
현재 내가 있는 행/열은 좌우에 -2, 2 를 곱해서 더 크게 가중치를 두고, 그 위아래 열/행에는 -1, 1 을 곱해서 작은 가중치로 계산한다.
이러면 내가 있는 행/열 주변의 변화량을 같이 반영하기 때문에 천천히 변하는 경우도 검출할 수 있다.
이와 유사하게 Scharr 은 아래와 같은 마스크를 사용한다.

Gaussian and multi-scale effect / LoG
그런데 이런 기존의 edge detector들도 여전히 문제가 있었다.
이런 미분을 사용하다보면, 노이즈가 있을 때 그 노이즈들 하나하나에 대해 엣지로 검출해서 그런 노이즈까지 디텍트가 너무 잘 되는 경우가 발생할 수도 있다. 이건 1차미분보다 2차 미분일 때 영향을 더 많이 받는다.
2차 미분값을 쓰려고 하면 증폭이 되기 때문이다.
따라서 노이즈에 의한 증폭을 막기 위해 노이즈를 흐리게 만들고자 가우시안 스무딩을 하게 된다.
그래서 이 가우시안 필터를 이용해서 이미지를 전처리하고나서 edge detector를 사용하면 더 정확하게 엣지를 검출할 수 있다.

가우시안 필터를 쓸 때는 시그마 값이 쓰이는데, 이 값이 클수록 더 많이 흐려진다.
이를 조합하면 다음과 같은 LoG Operator를 얻을 수 있다.
LoG는 Laplacian - of - Gaussian 의 축약으로, 가우시안으로 흐리게 만든 뒤에, 라플라시안 방식을 적용해서 제로크로스를 통해 엣지를 검출하는 방식이다.

라플라시안은 위와 같은 행렬을 사용한다.
따라서 가우시안과 라플라시안을 합치면

위와 같이 쓸 수 있다.

기하학적으로는 위와 같은 변환과정을 거친 뒤, 제로 크로싱을 찾아서 엣지를 검출한다.
Canny-Edge Detector
최근 가장 자주 사용되는 엣지 디텍팅 방식이다.
기존 방식과 달리 좋은 검출 방식의 기준을 아래와 같이 3가지로 두었다.

이걸 다르게 표현하면

이렇게 표현된다.
1번은 어쨌든 false 로 틀리게 검출하는 것 (엣지인데 아니라고 검출하거나, 엣지가 아닌데 엣지라고 검출하거나) 을 최소화 해야 한다는 의미, 2번은 굵기에 대한 기준 단위가 필요하다는 것. 3번은 검출된 엣지가 가능한 진짜 엣지에 가까워야 한다는 것이다.

캐니 엣지 방식을 사용하는 과정은 위와 같다.
1. 가우시안 스무딩으로 전처리
2. 소벨 방식을 통해서 1차로 엣지 디텍팅, 그리고 엣지 크기를 검출
3. 그 결과에 비최대 억제를 적용해서 작은 두께의 엣지 맵을 생성
4. 임계값 보다 작은 크기의 두께는 모두 제거 (거짓 검출된 엣지로 간주)

이때 비최대억제는 3x3 행렬의 가운데 값을 봤을 때, 이 값이 주변 8개 칸의 값과 비교해서 제일 큰 값이면 그대로 유지하고, 아니라면 0으로 설정하는 방식이다.

위와 같이 변환된다.
(그런데 이 그림에서 3행 2열의 값은 0이 되는 게 맞는 것 같다.)

그리고 그 결과로부터 엣지의 방향도 파악할 수 있다.
이렇게 검출한 엣지 중에서 false-positive를 검출해서 제거하기 위해, 캐니엣지는 2개의 threadhold 값을 사용한다.

이렇게 T high 와 T low 라는 값을 사용하는데, T high 보다 큰 경우에는 strong edge로서 검출한다.
T high 와 T low 사이는 weak edge 로서 만약 T high 보다 큰 엣지와 연결되어 있다면 엣지로 보고, T low와 연결되어 있다면 엣지가 아닌 것으로 본다.
그리고 T low 보다 작은 부분은 모두 엣지가 아닌 것으로 본다.
'CS > HCI 윈도우즈프로그래밍' 카테고리의 다른 글
| [Computer Vision] 7. Matching & Geometrical alignment (0) | 2024.06.11 |
|---|---|
| [Computer Vision] 6. Feature Detection (4) | 2024.06.09 |
| [Computer Vision] 4. Geometry Primer (3) : Transform (0) | 2024.06.02 |
| [Computer Vision] 3. Geometry Primer (2) : Homography (0) | 2024.05.31 |
| [Computer Vision] 2. Geometry Primer (1) : Homogeneous Coordinates (3) | 2024.05.31 |
