Link State
링크 스테이트 방식은 말 그대로 각 라우터가 자신이 알고있는 '링크 정보' = '링크 스태이트' 를 모두 공유해서 같은 네트워크 맵을 보는 상태를 만들고, 이 맵을 input으로 다익스트라 알고리즘을 돌려서 최단 경로를 얻는 방법이다.
다익스트라 알고리즘은, 시작점이 고정되어있을 때, 그 시작점으로부터 다른 모든 목적지까지의 최단경로를 구하는 알고리즘이다.
따라서 각각의 라우터는 자신을 시작점으로 해서 다익스트라를 돌리면 다른 모든 라우터까지의 최단 경로를 알 수 있다.
이를 통해 포워딩 테이블을 만든다.

LS 알고리즘을 설명할 때 위와 같은 노테이션을 사용한다.
Cxy는 x에서 y로 가는 비용을 말하며, 직접 연결된 링크가 없으면 무한대 값을 갖는다.
D(v)는 현재 측정한 v까지 가는 최소 비용 (최단 거리) 이다.
p(v) 는 v로 가는 경로에서 v의 직전 노드를 말한다. 이 정보를 이용해 '경로'를 알 수 있다.
N' 는 최단 경로를 찾은 노드를 이렇게 표시할 것이다.

알고리즘의 과정을 수도코드로 나타냈을 때, 초기화 돤계는 위와 같다.
먼저 N' 집합에 u 라는 시작점을 넣는다. 시작점은 최단경로가 이미 자기 자신으로 존재한다.
이때 나머지 모든 노드 v에 대해서 u와 인접한 노드들은 그 link state 를 D(v)로 저장한다.
물론 이 값이 v로 가는 최단 거리가 되지는 않을 수 있다.
인접하지 않았다면 무한대로 설정한다.

이제 모든 노드에 대한 최단 경로를 찾을 때까지 (즉, N'에 모든 노드가 들어갈 때까지) 반복한다.
각 반복에서 N' 에 없는 노드들 중에 지금까지 최단경로가 제일 짧은 노드 w, 즉 D(w)의 값이 제일 작은 노드를 찾는다.
그 노드로 가는 최단거리는 이제 그 D(w) 값이 되었으니, 이 노드 w를 N'에 추가해주고, 새로 발견한 최단 경로를 토대로 나머지 모든 노드 v에 대해 D(v)를 업데이트 해준다.
이때 업데이트하는 값은 기존 D(v) 값과, D(w) + Cw,v 를 비교해서 더 작은값으로 업데이트한다.
(기존 최단 거리냐, 새로 알게된 w까지의 최단 거리 + w에서 v까지 비용이냐)
이때 이 방법으로 최단 경로를 찾을 때는 코스트가 음수이면 안된다는 제약 조건이 필요하기는 하다.
하지만 코스트가 음수인 경우는 없으니 문제는 없다.
즉, N'에 들어간 노드 중에 그 노드로 가는 더 짧은 경로가 나중에 알려질 일은 없다.
이제 이 알고리즘을 직접 실행해보자

위와 같은 그래프에서 u를 시작점으로 돌린다고 해보자.
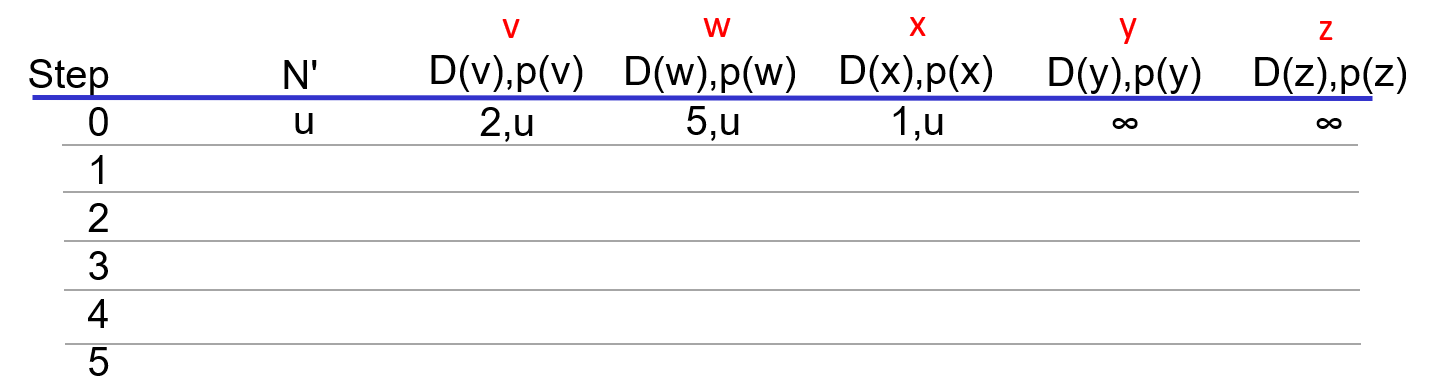
그러면 u와 인접한 노드들 중 링크가 존재하는 노드들의 거리 D() 를 업데이트 하고, 업데이트된 노드들은 p() 도 u로 업데이트 해준다.
알고리즘에서 7번째 줄까지 실행한 초기화 단계를 실행한 것이다.

이제 첫번째 반복문으로 들어온다.
먼저 지금까지 저장한 D() 중에 제일 짧은 거리를 찾는다.
그러면 x 노드가 선택되어 N'에 들어온다.
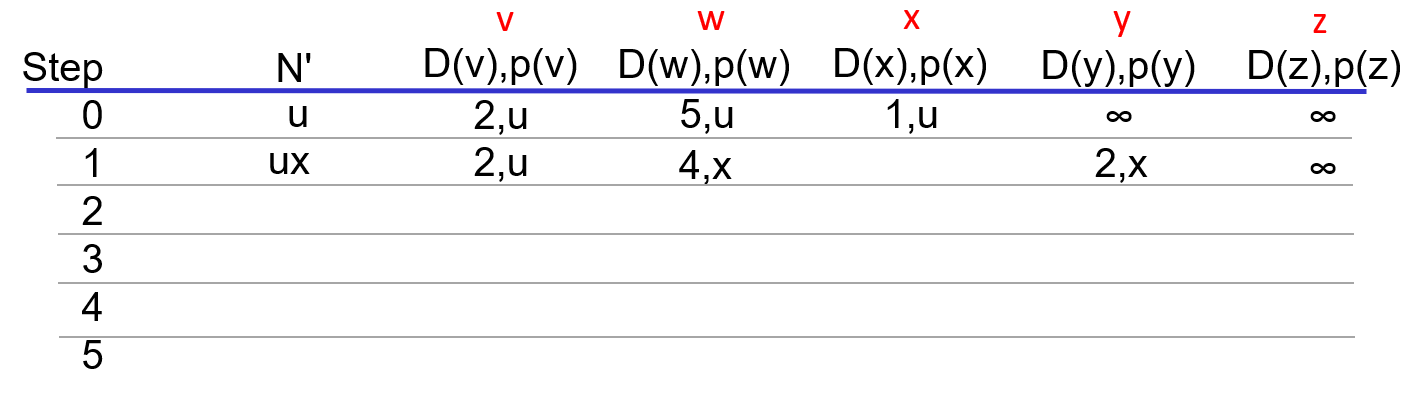
x와 인접한 노드들에 대해 그 최단 경로를 업데이트 해준다.
w의 경우, u에서 바로 오는 것보다, x를 거쳐서 가면 더 비용이 줄어드니 업데이트 해주고, 업데이트가 되었으니 p()도 업데이트 해준다.
y의 경우도 업데이트 되었고, x 자기 자신의 업데이트는 수행하지 않는다.

다음 단계로 가면 이제 다시 가장 작은 D()를 찾아서 y가 선택된다. (v를 골라도 상관없다.)
y를 N'에 추가해주고 같은 과정을 반복한다.

N'에 추가된 노드들은 제외하고 채우면 위와 같이 채워진다.
w, z 가 새로 업데이트 되었다.
이후부터는 설명을 생략하고 이미지만 나타냈다.





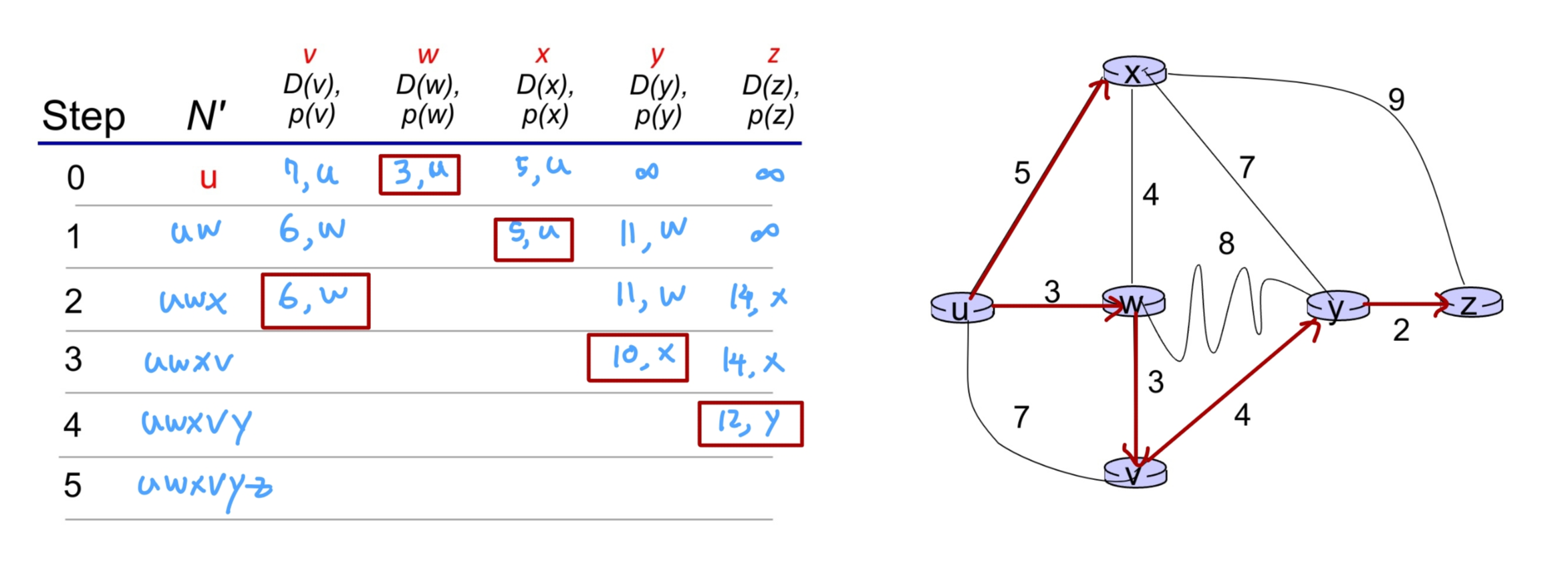
이 과정을 거치면 최종적으로 아래와 같이 경로가 나온다.

그러면 이 경로를 토대로 포워딩 테이블을 만들 수 있다.

v의 경우는 u에서 직접 가고, 나머지 경로는 모두 x를 경유하도록 한 것이다.

두번째 예제도 있는데, 이건 중간 과정은 생략하고 직접 해본 결과만 정리했다.

Link State 방식의 시간복잡도
다익스트라 알고리즘의 시간복잡도를 간단하게 계산해보자.
모든 노드의 개수가 n개 있다고 할 때, 반복문을 돌릴 때마다 하나의 새로운 노드가 N'에 들어가므로, 총 n-1번의 반복문을 돈다. 즉, O(n) 이다.
각각의 반복문 안에서는 D(w)의 최소값을 찾는다.
이때 N'에 없는 노드들에 대해 비교를 하니까, 비교횟수는 N부터 시작해서 1씩 감소한다.
따라서 n번 비교, n-1번 비교, ..., 이렇게 감소하므로, 러프하게 생각하면 1부터 n까지의 합으로 생각할 수 있어서 O(n²) 으로 생각할 수 있다.
여기에 우선순위 큐를 쓴다면 O(n log n)으로 줄일 수 있다.
여기에 더해 message complexity도 생각해보자.
LS 방식의 특징은 각 노드가 자신이 알고있는 링크 정보를 전체 라우터에게 보낸다. (브로드캐스트)
그러면 나라는 하나의 노드를 출발해서 모든 노드가 정보를 받기까지 몇개의 링크를 거쳐서 받을 수 있는지 궁금하다.
사실 이건 edge 개수에 영향을 받는다.
그런데 엣지 개수와 노드 개수는 상관관계가 있다.
모든 노드를 다 연결하면, 노드 개수의 제곱인 n² 정도의 링크가 필요하다.
하지만 굳이 그럴 필요가 없다.
만약 어떤 노드 b 가 노드 a의 정보를 2군데 이상의 경로를 통해 받을 수 있을텐데, 그러면 두번째 받은 정보는 무시하고 첫번째 받은 정보만 이용하고 다른 노드에게 보낼 것이다.
이런식으로 중복되는 정보는 퍼지지 않게 하는 식으로 동작시키면 O(n) 만큼의 링크 크로싱이 발생한다.
n개 노드가 이를 반복하므로 O(n²) 의 message complexity가 필요하다.
Route Oscillations
LS 방식이 만약 링크 코스트를 산정할 때, 트래픽 볼륨을 기반으로 코스트를 산정한다면 마치 괘종시계의 추가 왔다갔다하듯 경로가 한쪽으로 쏠리는 현상이 왔다갔다 반복될 수 있다.
트래픽 볼륨을 기반으로 코스트를 산정하는 것은 네비게이션을 생각하면 된다.
어떤 유명한 관광지에 차를 타고 가는데, 모든 사람들이 같은 내비게이션을 사용하고 있다고 해보자.
이 내비게이션이 어떤 고정된 경로만을 보여주면, 그 경로에 차가 몰릴테니, 실시간 트래픽을 반영하여 동적으로 경로를 알려준다고 했을 때, 아래와 같은 예시를 보자.

처음에는 모든 경로의 비용이 0이었다.
그리고 d, c, b 위치로 각각 1, e, 1 대의 차가 추가로 들어오고 있는 상황이다.
(e는 에코라고 부르며, 1보다 작은 양수를 말하지만, 일단 자동차의 대수로 생각해보자.)
처음에는 모든 경로의 비용(트래픽)이 0이기 때문에 위와 같은 경로를 보여준다.
d로 들어온 1대의 차는 a까지 0의 비용으로, b로 들어온 차는 a까지 0의 비용으로, c로 들어온 e대의 차는 a 까지 1의 비용으로 간다. (기존에 b, d 에서 1대의 차가 이미 가고 있었으므로, 어디를 고르든 상관없다.)
따라서 각 경로의 비용이 c에서는 a로가는데 1+e 가 걸리고, b, d 에서는 a로 가는데 1의 비용이 필요한 것으로 바뀔 것이다.

그런데 이 상태 이후로 d, c, b 에 계속해서 1, e, 1 대의 자동차가 내비게이션을 키고 들어오면 그때는 이렇게 경로가 바뀐다.
c로 들어오는 자동차 입장에서는 c 에서 d로 가는 비용이 0이었고, d에서 a로 가는 비용이 1이었기 때문에 d를 경유해서 a로 간다.
b로 들어오는 자동차 입장에서도, c로 들어온 e대의 자동차가 b-a 경로를 사용하는 바람에 비용이 1+e가 되어, c-d-a 방향으로 틀어서 가는 것이 더 짧은 비용으로 계산되어 위 그림과 같이 돌아가게 된다.
그러면 그 결과로 각 링크의 코스트가 위와 같이 바뀐다.

이렇게 링크 코스트가 바뀐 상태에서 꾸준히 d, c, b 로 차가 1, e, 1 만큼 들어온다면 이제는 거꾸로 반대로 몰리는 방향으로 길을 안내해주면서, 경로가 다시 위와 같이 바뀐다.

그리고 이렇게 양끝단으로 몰리는 과정이 계속 반복되게 된다.
마치 추가 왔다갔다하는 것과 비슷하다.
이 현상은 LS가 전체 그래프 맵을 가지고 각자 동일 알고리즘을 통해 경로를 계산하기 때문에 발생한다.
'CS > 컴퓨터 네트워크' 카테고리의 다른 글
| [컴퓨터 네트워크] 35. Network Layer (11) : intra-ISP routing protocol (OSPF) (0) | 2024.06.14 |
|---|---|
| [컴퓨터 네트워크] 34. Network Layer (10) : Distance Vector (2) | 2024.06.08 |
| [컴퓨터 네트워크] 32. Network Layer (8) : control plane, 라우팅 프로토콜 개요 (0) | 2024.06.08 |
| [컴퓨터 네트워크] 31. Network Layer (7) : Middlebox (0) | 2024.06.07 |
| [컴퓨터 네트워크] 30. Network Layer (6) : Generalized Forwarding (0) | 2024.06.06 |
