다음 2개의 명제가 참인지 거짓인지 생각해보자.
1. DFA가 받아들이는 언어는 유일하다. (O)
DFA가 받아들이는 (생성하는) 언어는 유일하다.
(그리고 그 언어는 regluar 하므로, regular language 라고 할 수 있다.)
2. Regular Language 가 주어질 때, 이 언어를 만드는 DFA는 유일하다. (X)
이 명제는 위 명제의 역인데, 이 명제는 틀렸다.
하나의 언어를 받아들이는 (만드는) DFA는 여러개가 존재할 수 있다.
같은 언어를 만들어내는데, 10개 state로 구성된 DFA를 만들 수도 있고, 20 state 로 구성된 DFA를 만들 수도 있다.
따라서 이로부터 어떻게 하면 같은 언어를 만들더라도 최소한의 상태를 사용해서 만들 수 있을지 고민할 수 있다.

왼쪽의 DFA를 보면 q5 라는 상태는 그 상태로 들어오는 edge가 없다.
따라서 q5는 init state에서 출발하는 경우 절대 도달할 수 없다.
이런 state를 가리켜 inaccessible states 라고 부르며,
이런 state는 minial DFA를 만들 때 지울 수 있다.
이제 q5 state 를 제거하고 왼쪽 DFA를 다시 살펴보면, q0 에서 분기되는 위쪽 state와 아래쪽 state가 서로 대칭임을 알 수 있다.
q0에서 0을 받았을 땐 상단부, 1을 받았을 때는 하단부로 가지만 어디로 가든 그 이후 동작이 비슷하다.
그래서 이 동작을 하나로 합친 형태가 오른쪽에 보이는 그래프이다.
따라서 위의 두 DFA는 같은 언어를 받아들이는 DFA지만 오른쪽 그래프가 훨신 적은 state로 이루어져 있음을 알 수 있다.
이렇게 합쳐서 줄일 수 있는 state를 redundant states 라고 부른다.
이제 regular, equivalent 에 이어 DFA와 관련하여 표현할 수 있는 새로운 용어를 정의한다.
하나의 DFA를 구성하는 어떤 두 state p, q 에 대해 모든 종류의 문자열 w가 주어질 때,
항상 𝜹*(p, w) = 𝜹*(q, w) 인 경우 indistinguishable 하다.
(결과는 final, non-final 모두 상관없다.)
반대로 문자열 w에 대해 𝜹*(p, w) ≠ 𝜹*(q, w) 인 문자열이 하나라도 존재하면, 이 둘은 distinguishable 하다.
즉, 어떤 두 스테이트로부터 w라는 같은 문자열이 주어졌을 때 둘 다 같은 답을 말한다면 구별할 수 없고, 다른 답을 말하면 구별할 수 있다는 것이다.
이 두 조건은 모든 state 쌍에 대해 둘 중 하나로 반드시 나뉘므로 DFA의 임의의 두 state는 반드시 distinguishable 하거나, indistinguishable 하다.
이때 indistinguishable state 집합에 대해 equivalance class 라고 말할 수 있다.
equivalance class는 특별한 성질을 갖는 '집합' 으로 다음 3가지 조건을 만족해야 한다.
1. 집합의 원소는 자기 자신끼리 관계를 가져야 한다.
indistinguishable state 에 대해서 같은 state p와 p는 항상 같은 결과로 도출되므로 당연히 구별할 수 없다.
2. x1 과 x2 가 관계를 가지면, x2와 x1 도 관계를 가진다.
indistinguishable state 에 대해서 p와 q가 구별할 수 없다면, q와 p도 구별할 수 없으므로 성립한다.
3. x1과 x2 가 관계를 가지고, x2와 x3이 관계를 가지면, x1과 x3도 관계를 가진다.
indistinguishable state 에 대해서 p와 q가 구별할 수 없고, q와 r도 구별할 수 없다면 q와 r도 구별할 수 없다.
그리고 이 성질을 사용하면, equivalance class 안에 있는 모든 상태를 하나의 상태로 바꿀 수 있다.
예제 문제를 보면서 주어진 DFA를 equivalent한 min DFA로 바꾸는 과정을 살펴보자.
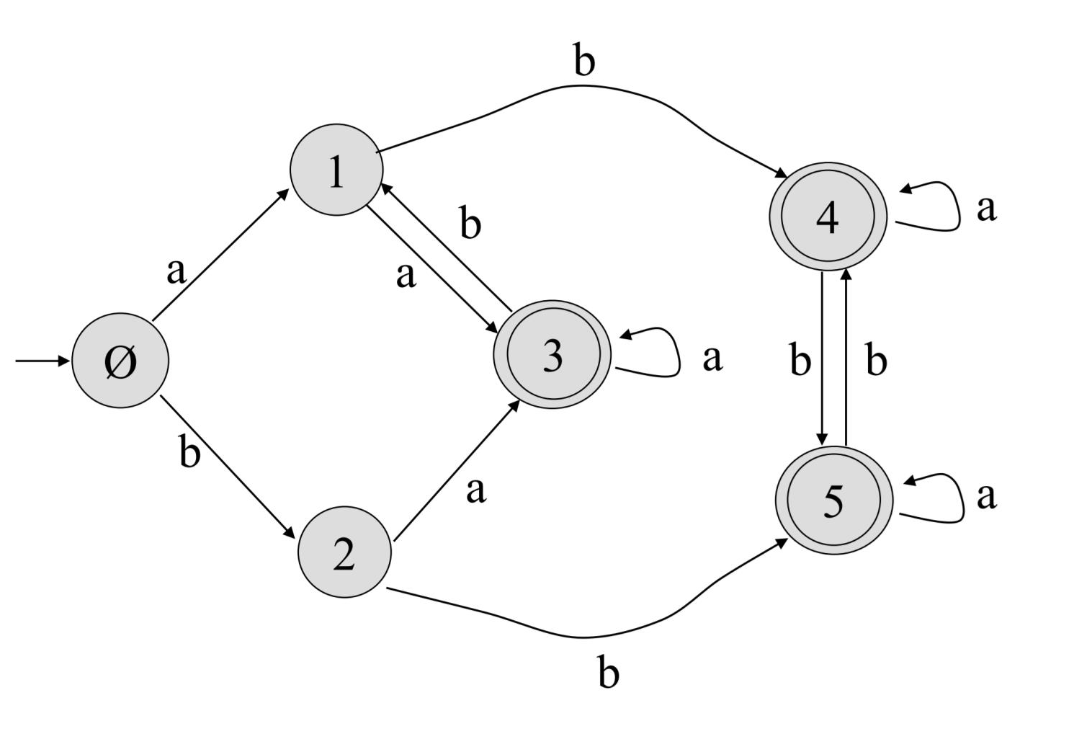
먼저 주어진 DFA에 임의의 문자열을 넣어보면서 indistinguishable한 상태들을 찾아본다.
사실 정의에 의하면 가능한 모든 문장을 다 넣어봐야 하지만, 일단 간단한 문장부터 넣어보자.
제일 간단한 문장은 당연히 비어있는 문자열 λ 이다.
위 DFA에 λ를 넣으면 0번 state에서 멈추며 이곳은 non-final state 이다.
따라서 λ는 이 DFA가 받아들이는 문장이 아니다.
이 비어있는 문자열을 모든 상태에 다 넣어보면 주어진 상태들을 반환하는 결과에 따라 2가지로 분류할 수 있다.
{0, 1, 2} => non-final
{3, 4, 5} => final
따라서 주어진 state 들을 이렇게 2개의 파티션으로 나눌 수 있다.

이때 λ에 대해 같은 결과를 냈다고 해서 {0, 1, 2}, {3, 4, 5} 가 equivalnce class 라는 보장을 할 수 없다.
(모든 문자열에 대해 해본 것이 아니기 때문이다.)
하지만 적어도 P₁ 에 존재하는 state와 P₂ 에 존재하는 state는 서로 서로 구분이 된다는 것을 보장할 수 있다.
다음으로 P₁, P₂ 에 들어있는 각각의 state에 대해서 추가적으로 구별이 되는지 여부를 테스트해보자.
이번에는 길이가 1인 문자열 a, b 를 각각 넣어본다.
그러면 다음과 같이 구분된다.

상태3에서 a 를 넣으면 3으로 되돌아온다. 3은 P₁ 에 속한 상태이므로 P₁ 상태를 유지한다고도 볼 수 있다.
상태3에서 b 를 넣으면 1로 이동한다. 1 은 P₂ 에 속한 상태이므로 P₂ 로 상태가 바뀐다고도 볼 수 있다.
이를 각각의 상태에 모두 해보면 위와 같은 결과가 나온다.
이때 입력 a, b는 모두 주어질 수 있는 입력이므로 이 2가지 '조합'을 기준으로 같은 것끼리 다시 묶어볼 수 있다.
(이 조합이 같다면 그 조합이 같은 것들에 대해서는 구별할 수 없기 때문이다)

그러면 다음과 같이 표현할 수 있고, 이를 통해 적어도 state 3은 state 4, state 5와는 구별된다는 것을 보장할 수 있다.
이제 P₁₁ 과 P₂₁ 을 구성하는 state 는 1개밖에 없으므로 이들에 대해서는 구별이 되는지 안되는지 따져볼 수 없다.
나머지 P₁₂ 와 P₂₂ 에 대해서 구별이 되는지 여부를 추가젹으로 따져보자.
지금까지는 길이가 1인 문자열로 구별 여부를 나누어보았으니, 여기에 문자를 하나 더 추가하여 길이가 2인 문자열로 구별되는지 따져볼 수 있다.
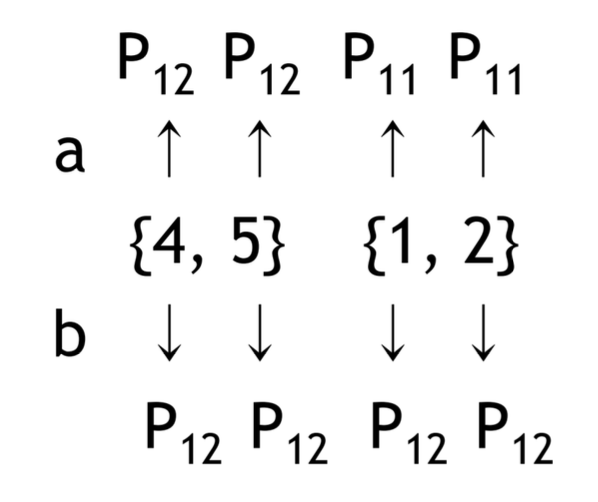
이 결과를 보면, {4, 5} 는 길이가 2인 문자열에 대해 자신이 속한 파티션으로 분류가 되므로 여기에 길이가 몇 인 문자열을 더 붙이더라도 더 이상 구분이 되지 않음을 알 수 있다. 따라서 {4, 5} 는 하나의 상태로 합칠 수 있다.
{1, 2} 에 대해서도 둘 다 동일하게 기존의 새로운 파티션이 아니라 이미 존재하는 파티선 P₁₂ 와 P₁₁ 로만 이동하므로 여기서 더 나눠질 수 없다.
따라서 4, 5 상태와 1, 2 상태를 하나로 묶어서 다음과 같이 DFA를 그릴 수 있다.

연습 문제

주어진 그래프를 minimal DFA 로 만들어보자.

먼저 λ를 넣어서 각 상태를 다음과 같이 파티션으로 나눌 수 있다.
각각의 상태에 대해 각 파티션이 equivalent class 가 되는지 확인해보자.

그림과 같이 나타내면 { 1, 3 } 만 그룹으로 남는다.
그런데 이 그룹에 대해서는 항상 P₁₁ 로 가므로 equivalent class 이다.
따라서 다음과 1, 3 상태를 묶어서 다음과 같이 DFA를 그릴 수 있다.

'CS > 오토마타' 카테고리의 다른 글
| [오토마타] 8. Regular Expression 과 Regular Language (0) | 2024.10.23 |
|---|---|
| [오토마타] 7. Regular Expression (0) | 2024.10.23 |
| [오토마타] 5. NFA (Nondeterministic Finite Accepter) (0) | 2024.10.20 |
| [오토마타] 4. DFA (Deterministic Finite Accepter) (0) | 2024.10.17 |
| [오토마타] 3. 오토마톤 (0) | 2024.10.17 |
