지금까지 DFA에 대해서 정리하면서, DFA로 표현할 수 있는 언어를 regular language 라고 했었다.
이때, 모든 NFA는 DFA로 변환이 가능하기 때문에 NFA로 표현할 수 있는 언어 역시 regluar language 였다.
DFA로 표현가능한 언어가 regular language 라면, 거꾸로 regular language 는 DFA로 표현이 가능하다.

따라서 위 그림과 같은 관계가 성립한다.
이번 글에서는 regular language를 나타내는 또 다른 방법인 regular expression 에 대해 정리해본다.
regular expression 은 다음 3가지 내용으로 정의된다.
1. φ, λ, a ∈ Σ (알파벳에 포함되는 하나의 심볼) 3가지는 모두 regluar expression 이다.
이 regluar expression 들을 가리켜 primitive regular expression 이라고 부른다.
2. 만약 r₁ 과 r₂ 가 regluar expression 이라면 다음도 모두 regluar expression 이다.
r₁ + r₂, r₁ · r₂, r₁*, (r₁)
3. 2에서 정의한 기호를 유한번 사용해서 만들 수 있는 문자열은 regular expression 이다.

이 사진은 regular expression 의 한 가지 예를 보여준다.
우선 의미보다는 이렇게 생긴 것이 regular expression 이라는 것만 기억하자.

이 표현은 regular expression 이 아니다.
+ 기호를 사용하려면 그 양 옆 regular expression 이 존재해야 한다.
regular expression 은 regular language 를 나타내는 또 다른 방법이라고 했었다.
이를 일반화하여, regular expression r 을 사용하여 나타내는 언어를 가리켜 L(r) 이라고 한다.
(L(G), L(M) 이어서 r 을 통해서 L을 나타내는 것이다.)
이제 위에서 정리한 regular expression 기호들의 의미를 정리해보자.
φ : 공집합
λ : { λ }
공집합은 기계로 보면 어떠한 문자열도 문장으로 받아들이지 않는 것을 의미한다.
(기계로는 transition 이 없는 non-final state로 이루어진 기계를 생각하면 된다.)
반면 { λ } 는 '빈 문자열' 이라는 문자열은 문장으로 받아들이겠다는 것을 의미한다.
(기계로는 transition 이 없는 final state 하나로 이루어진 기계를 생각하면 된다.)
a : Σ 에 속하는 모든 a 에 대해 { a } 는 a 하나만을 문장으로 갖는 언어라고 생각할 수 있다.

두 regular expression 에 대해서는 위와 같이 나타낼 수 있다.
L 은 '집합' 이라는 것을 기억하자.
r1 + r2 라는 regular expression 으로 나타내는 언어는 L(r1) ∪ L(r2) 와 같으며,
r1 · r2 라는 regular expression 으로 나타내는 언어는 L(r1)L(r2) 와 같다. (concatenation)
(r1) 은 그대로 괄호를 벗기면 되고, r1* 는 L(r1) 의 star closure 과 같다.
(언어에서 * 를 붙이는 것은 문장을 안가져오거나 (= λ), 하나만 가져오거나, 2개를 가져와서 서로 붙이거나, ... 하는 경우를 모은 것이다.)

간단한 예시를 보면, a * · (a+b) 라는 regular expression 을 통해 만드는 언어는 위와 같이 전개할 수 있다.
연습 문제

이 정규표현식으로 만들어지는 언어를 집합 표현으로 작성해보자.

(a+b)* 는 a 또는 b 로 구성된 모든 종류의 문자열을 말한다.
이 뒤에 a 또는 bb 를 붙이는 것이 이 정규표현식으로 나타낼 수 있는 언어이다.

다음으로 이 regular expression 이 나타내는 언어를 집합 기호로 작성해보면
(aa) 를 0번 이상 사용하고, 그 뒤에 (bb) 를 0번 이상 사용하고, 그 뒤에 b 를 붙인 문자열이 문장이 되는 언어이다.
따라서
{ b, aab, aaaab, .... , bbb, bbbbb, ...., aabbb, aaaabbbbb, .... } 와 같은 문자열을 문장으로 갖는다.
이를 조합하면 a를 짝수번 사용하고, b를 홀수번 사용해서 나타내는 문장이 되겐다.

이번엔 거꾸로 집합 기호로 문장이 주어졌을 때, 이 언어를 나타낼 수 있는 정규표현식을 찾아보자.
위 기호는 0, 1 로 구성된 문장 w 중에서, 0이 한번이라도 연속적으로 등장해야하는 문자열을 문장으로 갖는 언어를 나타낸다.
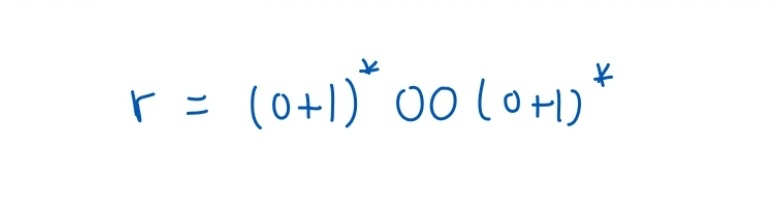
위와 같이 나타낼 수 있다.
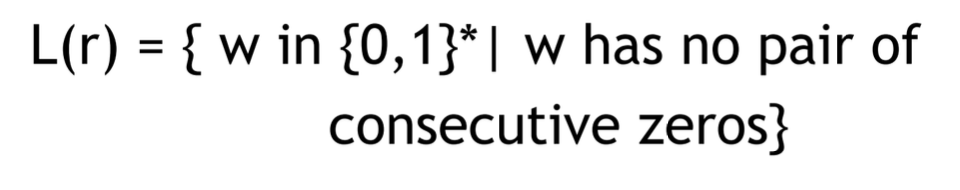
이번엔 반대로 연속적인 0이 없어야 한다는 조건을 나타내고 있다.
이 문제는 여러가지 풀이가 있다.
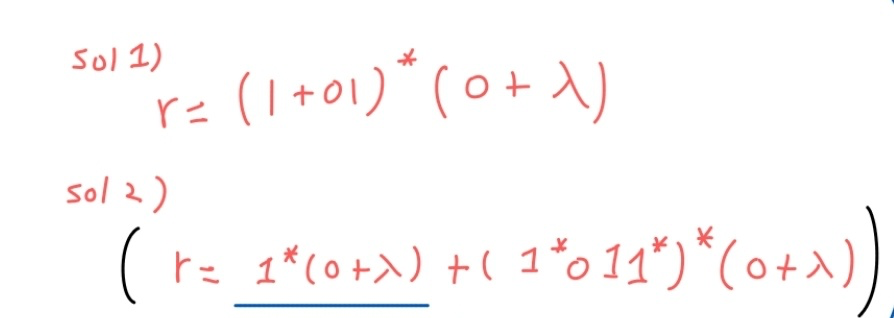
이렇게 2가지 풀이를 생각할 수 있다.
(답은 무한가지다. 하나의 언어를 표현할 수 있는 DFA가 무수히 많은 것처럼)
'CS > 오토마타' 카테고리의 다른 글
| [오토마타] 9. Regular Grammar (0) | 2024.10.23 |
|---|---|
| [오토마타] 8. Regular Expression 과 Regular Language (0) | 2024.10.23 |
| [오토마타] 6. FA 에서 state 개수 줄이기 (0) | 2024.10.22 |
| [오토마타] 5. NFA (Nondeterministic Finite Accepter) (0) | 2024.10.20 |
| [오토마타] 4. DFA (Deterministic Finite Accepter) (0) | 2024.10.17 |
