
지난 글에서 DFA로 나타내는 언어는 regular language 이며, regular language 는 DFA로 나타낼 수 있다고 하였다.
그런데 이 regular language 를 나타내는 방법 중 하나가 바로 regular expression 이었다.
따라서 위 그림과 같이, regular expression 은 DFA / NFA 로 나타낼 수 있고,
반대로 DFA / NFA 가 나타내는 언어도 regular expression 을 통해 나타낼 수 있다.
이를 증명하려면, regular expression 이 나타내는 언어가 DFA가 만드는 언어의 superset 이고,
반대로 DFA 가 만드는 언어가 regular expression 이 나타내는 언어의 superset 임을 보이면 된다.
그러면 regular expression 은 언어를 DFA를 가지고 나타내는 언어를 표현하는 또 다른 수단이 된다.
먼저 어떤 regular expression 이 있다고 할 때, 반드시 regular language 가 있다는 것을 보이자.
반드시 regular language가 존재한다는 것은 반드시 DFA / NFA 가 존재한다는 것과 같은 말이다.

먼저 이를 증명하기 위해, primitive regular expression (φ, {λ}, {a}) 3가지를 모두 NFA로 나타낼 수 있다는 것을 직접 그래프를 그래서 보일 수 있다.
먼저 φ 를 받아들이는 NFA는 init state 에 어떤 transition 도 없고, init state = non-final state 이면 된다.
{λ} 를 받아들이는 것은 NFA 기준으로는 λ 로 이동하는 transition 이 존재하여 final state 로 갈 수 있다고 볼 수 있고,
{a} 를 받아들이는 것은 NFA 기준으로는 a 로 이동하는 transition 이 존재하여 final state 로 갈 수 있다는 것과 같다.
이렇게 primitive regular expression 에 대해 NFA 가 존재함을 보였으니 regular expresion 의 기본 연산
덧셈, · , *, ( ) 에 대해서도 NFA를 통해 나타낼 수 있음을 보이면 된다.
이를 보이는 핵심 아이디어는 모든 regular expression을 표현하는 모든 NFA는 1개의 init state와 1개의 final state를 갖도록 만들 수 있다.
만약 여러개의 final state를 가진 NFA라면, 모든 final state를 non-final state로 만들고, 그 state 들에 대해서 하나의 final state로 가는 λ 트랜지션을 만들면 1개의 final state를 갖는 NFA로 만들수 있다.
이를 그래프로 나타낸 것이 아래와 같다.

그리고 그림에서 보는 것처럼 이 아이디어를 활용하면 M(r1), M(r2) 라는 r1, r2 에 대한 기계를 모두 받아들이는 하나의 기계를 만들어낼 수 있다. 각 M(r1), M(r2) 의 final state를 non-final state로 만들고, λ 트랜지션을 통해 하나의 final state로 가도록 만든다.
따라서 이 그림을 통해 r1 + r2 역시 NFA로 나타낼 수 있음을 보였다.

다음으로 concatenate 의 경우 위와 같이 직렬로 두 기계를 이어서 NFA로 나타낼 수 있다.

star closure도 위와 같이 λ 트랜지션을 두면 나타낼 수 있다.
이를 통해서 모든 regular expression 은 NFA로 나타낼 수 있음을 알 수 있다.
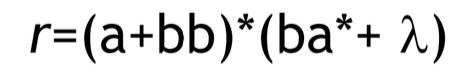
다음 regular expression 을 받아들이는 NFA를 한번 그려보자.

왼쪽은 (a+bb) 를 나타낸 NFA 이고, 오른쪽은 (ba* + λ) 를 나타내는 NFA 이다.
각 NFA에 대해 위에서 정리한 NFA 변환을 사용하면

이렇게 하나의 final state를 갖는 NFA로 만들 수 있다.
이제 거꾸로 NFA가 주어졌을 때 이 NFA를 regular expression 으로 나타낼 수 있다는 것을 보여보자.
이때 NFA는 매우 다양한 형태가 들어올 수 있으므로, NFA의 형태를 equivalent 한 다른 형태의 NFA를 고민해보려고 한다.
그 전에 새로운 형태의 그래프인 Generalized Transition Graph 를 새로 정의한다.
줄여서 GTG 라고 부르는 이 그래프는, 기존의 transition graph 와 달리, edge 에 regular expression을 사용할 수 있는 그래프를 말한다. (NFA에서는 심볼 하나 또는 λ 만을 사용 가능했었다. & NFA도 GTG의 일부이다. )

다음과 같은 형태가 GTG 이다.
init state에서는 a를 계속해서 받을 수 있으니 a* 를 나타낸 것이고, 그 뒤에 a 또는 b를 받아서 이동한 뒤 c*를 반복적으로 받는 그래프이다. (c*를 반복적으로 받는 것은 c를 반복적으로 받는 것과 같다.)
가운데에 a+b 를 적은 것은 NFA 에서 a, b 라고 적었던 것과 동일하다.
이 그래프가 나타내는 언어를 regular expression 으로 표현하면 다음과 같다.
a* + a*(a+b)c*
왼쪽 state와 오른쪽 state 모두 final state 이므로, 각 final state 로 갈 수 있는 경우를 + 로 묶어서 나타낸 것이다.
GTG의 특별한 형태로 complete GTG 가 있다.

왼쪽은 그냥 GTG를 나타내고, 오른쪽은 Complete GTG를 나타낸다.
Complete GTG는 모든 엣지가 표현되어 있는 GTG를 말한다.
따라서 위 그림에서 표현되어있지 않은 엣지를 모두 φ (공집합) 기호를 통해 나타내면 equivalent 한 complete GTG가 된다.
(이때 φ 가 아니라 λ 를 사용하지 않도록 조심하자. λ는 '심볼 추가 없이 state 이동이 가능한 것' 이고 φ는 이동 자체가 불가능한 것을 말한다.)
complete GTG 에서는 각 state 마다 state 개수만큼의 outgoing edge를 가져야 한다.
따라서 전체 edge 의 개수는 상태 개수가 S 일 때, S² 과 같다.
이제 Complete GTG 로부터 Regular Expression 을 만드는 일반적인 방법을 고민해보자.
만약 이 방법을 터득할 수 있다면 NFA를 GTG로 만들고, 이를 Complete GTG로 만든 다음 regular expression 으로 변환하면 되므로 모든 NFA를 regular expression 으로 나타낼 수 있음을 보이는 것과 같다.

다음 그림은 1개의 init state 와 1 개의 final state를 갖는 Complete GTG 이다.
각 엣지에는 r1, r2, r3, r4 라는 regular expression 이 적혀있다고 하자.
이 그래프가 만드는 문장을 regular expression 으로 적어보면 다음과 같다.

우선 final state로 가려면 r1*r2는 반드시 거쳐야 한다.
그리고 final state로 간 이후에는 2가지 선택이 있다.
r4 로 제자리 걸음을 하거나, (+)
r3으로 돌아갔다가 다시 r1*r2 를 거쳐 되돌아오는 방법이다.
그리고 이 2가지 선택은 계속 반복할 수 있으므로 감싸서 * 로 표현한다.
이를 증명하기 위해 다음과 같이 일반화된 형태로 GTG를 그려보자.

rᵢᵢ 는 qᵢ 에서 qᵢ 로 가는 regular expression 을 나타내는 것이고, 나머지도 같은 의미로 출발 state와 도착 state를 나타낸다.
이때 qi 에서 출발해서 qj 로 가려면 반드시 rᵢⱼ 를 거쳐야만 한다.
따라서 다음과 같이 정규표현식을 나타낼 수 있다.

이때 1번 공간에는 아직 qj를 방문한 적 없는 qi 상태를 목적지로 하는 모든 표현이 와야 한다.
(위 정규표현식에서 rᵢⱼ 는 아직 qj를 방문하지 않은 상태에서 처음으로 qi 에서 qj로 넘어가는 것을 말한다.)
이 표현은 rᵢᵢ 말고는 없다.
2번 공간에는 qⱼ에서 qⱼ로만 가면 된다.
이 방법은 qi 를 거쳐서 qj로 돌아오거나, rⱼⱼ를 사용해서 다시 되돌아오는 방법 2가지가 있다.
따라서

이렇게 정규표현식을 쓸 수 있다.
이제 2개 state가 아니라 3개 state 를 갖는 Complete GTG를 변환해보자.
(final state가 꼭 하나여야 하나 하는 의문이 들었는데, 위에서 λ 를 활용하여 final state 의 개수를 1개로 만드는 방법을 소개하였으므로 final state 는 하나라고 전제할 수 있다.)
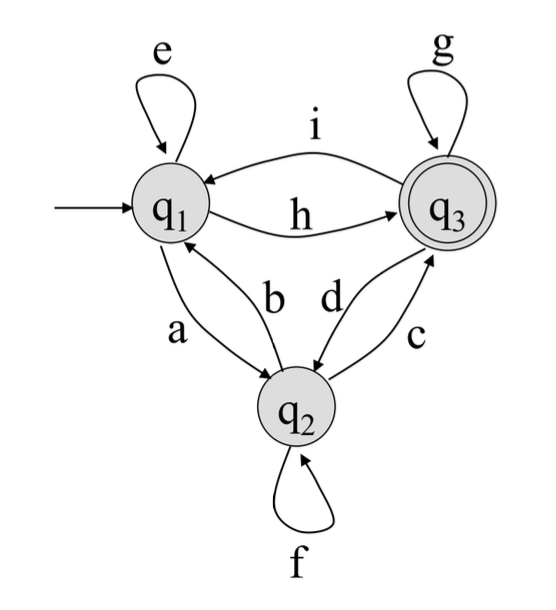
3개 상태를 갖는 Complete GTG는 이대로 표현하기 힘드니, 2개의 상태를 갖는 Complete GTG로 변환하여 표현한다.
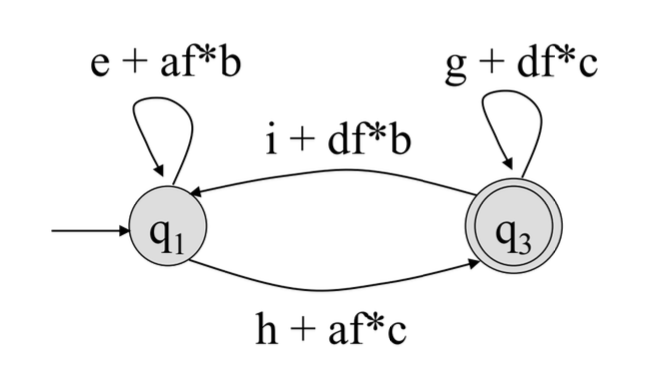
2개의 상태를 갖는 Complete 로의 변환은 그림과 같이 할 수 있다.
이를 다시 아까와 비슷한 방법으로 증명해보면

이렇게 i, j, k 첨자를 붙인 3개의 state에 대해서

새로운 ii, ij, ji, jj 를 표현할 수 있다.
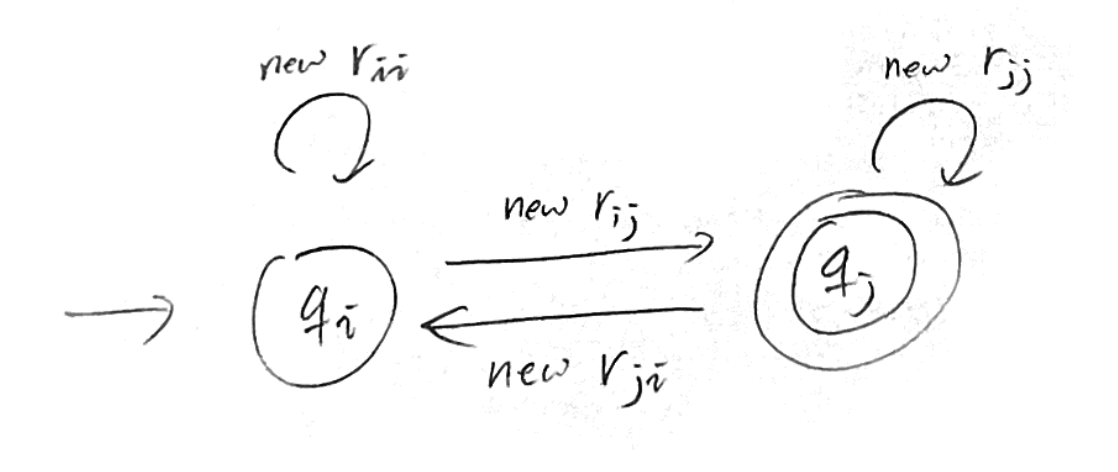
이들로 구성된 2개 state를 갖는 Complete GTG는 위와 같다.
이제 새로 정의한 ii, ij, ji, jj 를 하나씩 뜯어보자.
1. 새로 정의한 ii
기존의 ii 를 사용하거나, qj 상태를 건들지만 않으면 되므로, qk 상태로 이동했다가 kk 로 원하는 만큼 반복을 돌고 다시 ki 로 되돌아 오면 된다.
따라서 ii + (ik k* ki) 로 표현할 수 있다.
2. 새로 정의한 ij
기존의 ij 를 사용하거나 qk 를 거쳐서 qj 로 이동할 수 있다.
따라서 ij + (ik k* kj) 로 표현할 수 있다.
3. 새로 정의한 ji
기존의 ji 를 사용하거나, qk 를 거쳐서 qi 로 이동할 수 있다.
따라서 ji + (jk k* ki) 로 표현할 수 있다.
4. 새로 정의한 jj
기존의 jj 를 사용하거나, qi 를 건들지만 않으면 되므로 qk 로 가서 돌다가 되돌아오면 된다.
따라서 jj + (jk k* kj) 로 표현할 수 있다.
이렇게 2개 state를 갖는 Complete GTG 를 만든 다음에는 기존의 regular expression 을 만드는 공식을 활용하여 똑같이 regular expression을 만들어낼 수 있다.
이 과정을 N개 state를 갖는 Complete GTG에 대해 귀납적으로 적용할 수 있으므로, 모든 Complete GTG를 regular expression 으로 나타낼 수 있다. 이때 state 개수를 줄이다보면 점점 regular expression이 복잡해질 수 있다.

그때는 이 규칙을 사용하여 regular expression 을 간소화할 수 있다.
한가지 헷갈릴 수 있는 점은 rφ 인데, r이 나타내는 문장 하나와 공집합의 문장 하나를 꺼내서 concatenate 한다는 것은 정의할 수 없다.
따라서 그 결과는 공집합이다.
마지막으롱 공집합에서 문장을 꺼내서 λ 에 붙이는 과정을 반복하는 * 연산은 최초에 λ 에 붙이는 것을 반복하는 과정이므로 결국 λ와 같다.
모든 NFA는 init state, final state 가 각각 1개인 NFA로 나타낼 수 있고, 이 NFA의 트랜지션 그래프는 GTG에 속하며, 이 GTG를 Complete GTG로 변환하면 위 과정을 통해 regular expression 으로 반드시 만들 수 있다.
따라서 최종적으로 NFA가 주어졌을 때, 이 NFA는 언제나 regular expression 으로 바꿀 수 있다.
그리고 지금까지 이 과정을 거쳤던 이유는
regular expression 과 NFA (= regular language, DFA가 만드는 언어는 regular language 이므로) 사이의 관계를 보기 위함이었다.
모든 regular expression 은 NFA로 나타낼 수 있었고, 모든 NFA는 Complete GTG를 통해 regular expression 으로 나타낼 수 있었다.
따라서 regular expression 은 그에 상응하는 regular language 이 반드시 존재하며,
모든 regular language 역시 상응하는 regular expression 으로 나타낼 수 있다.
(즉 regular expression == regular language == NFA 이다.)
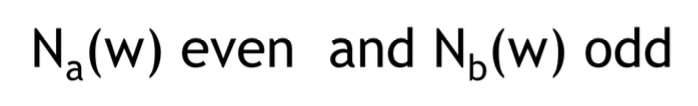
연습문제로, a 의 개수가 짝수이고, b의 개수가 홀수인 문장 w를 나타내는 regular expression 을 만들어보자.
먼저 주어진 언어가 regular 한지 아닌지는 알 수 없으나 regular expression 을 만들 수 있다는 것은 regular language 라는 것과 같다.
regular language를 나타낼 수 있다는 것은 곧 DFA, NFA 가 존재한다는 것과 같으므로 트랜지션 그래프를 먼저 그려보자.
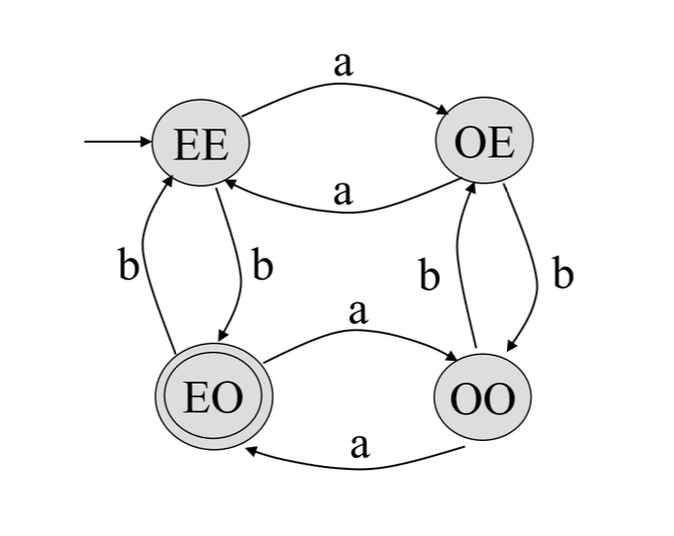
트랜지션 그래프는 위와 같이 그릴 수 있다.
각 상태는 a의 개수, b의 개수가 각각 짝수/홀수 중에 어떤 것인지를 나타낸다.
이렇게 NFA로 나타내었다는 것은 곧 regular 하다는 것과 같으니 이 언어는 regular language가 맞다.
이제 이 NFA로부터 regular expression 을 만들어보자.
그 과정은 Complete GTG를 만드는 것부터 시작한다.

그림과 같이 상태가 4개인 Complete GTG를 만들 수 있다.
이제 이 상태의 개수를 하나씩 줄여보자.
제거할 상태는 init state, final state 를 제외한 나머지 state 이다.

OE 상태를 제거하면 위와 같은 그림이 된다.
예를 들어 EE 에서 EO 로 가는 경우 regular expression 을 찾는다고 하면 다음과 같이 나타낼 수 있다.
1. 기존처럼 b만 하나 더해서 바로 가거나
2. OE를 거쳐서 OE에서 돌다가 OE에서 EO 로 가는 경우
1번은 b
2번은 aφ*φ = a λ φ = φ (φ이 concatenate에 포함되면 그냥 φ 이다.)
따라서 (b + φ) = b 로 쓸 수 있다.
위 그림에서 EE → EO 방향 트랜지션을 보면 여전히 b 인 것을 확인할 수 있다.
위와 같은 과정으로 OE를 포함하는 모든 경로를 제거하면 된다.
다시 여기에서 OO 상태를 제거하면

위와 같이 나타나고, 여기에 r1*r2(r4* + r3r1*r2) 라는 공식을 적용하면 regular expression 을 찾을 수 있다.
regular expression 은 실제로도 많이 활용된다.
예를 들어서 vi 에디터에서 특정 문장을 검색할 때, regular expression 을 검색 조건으로 넣을 수 있다.
이때 이 검색 조건에 맞는 문장을 찾을 때는 regular expression 을 DFA로 만들어서 yes/no를 판별하는 알고리즘을 작성하고,
이 알고리즘에 탐색 대상 문장을 심볼 바이 심볼로 넣어서 판별할 수 있다.
'CS > 오토마타' 카테고리의 다른 글
| [오토마타] 10. Regular Language 의 Closure Properties (0) | 2024.10.24 |
|---|---|
| [오토마타] 9. Regular Grammar (0) | 2024.10.23 |
| [오토마타] 7. Regular Expression (0) | 2024.10.23 |
| [오토마타] 6. FA 에서 state 개수 줄이기 (0) | 2024.10.22 |
| [오토마타] 5. NFA (Nondeterministic Finite Accepter) (0) | 2024.10.20 |
