Pruning Trees
지난 글에서 정리했던 브루트포스 & Score 함수를 이용한 motif 탐색 알고리즘은 시간이 매우 오래 걸렸다.
이는 각 Score 함수의 실행 시간은 짧았지만 motif 조합을 다 해봐야했기 때문에 Score 함수의 호출 횟수가 너무 많았기 때문이다.
하지만 모든 경우에 대해 매번 Score 함수를 호출해야만할까?
pruning tree 알고리즘을 사용하여 호출 횟수를 줄여보자.
이 알고리즘은 현재까지 발견한 최적해와 비교하여, 현재 하려는 계산이 더 최적이 될 것 같지 않을 때 굳이 계산해보지 않고 과감하게 건너뛰는 방법이다.
예를 들어보자.
10개의 DNA에서 공통적으로 등장하는 10-mer motif 를 찾으려고 한다.
이때 4개 DNA 에 대해서 점수를 계산했더니 17점이 나왔고, 이전 계산까지 찾은 가장 높은 점수는 79점 이었다.
이때 우리는 나머지 6개의 DNA 에 대해서 점수를 계산해볼 필요가 전혀 없다.
왜 그럴까?
만약 6개의 DNA에 대해서 10-mer 가 모두 동일하다면 이 6개에 대해서 6 * 10 = 60 점의 점수를 추가로 얻을 수 있다.
지금까지 계산한 결과 17점에 60점의 점수를 더해도 77점으로 79점을 넘을 수 없으므로 굳이 계산해볼 필요가 없다.
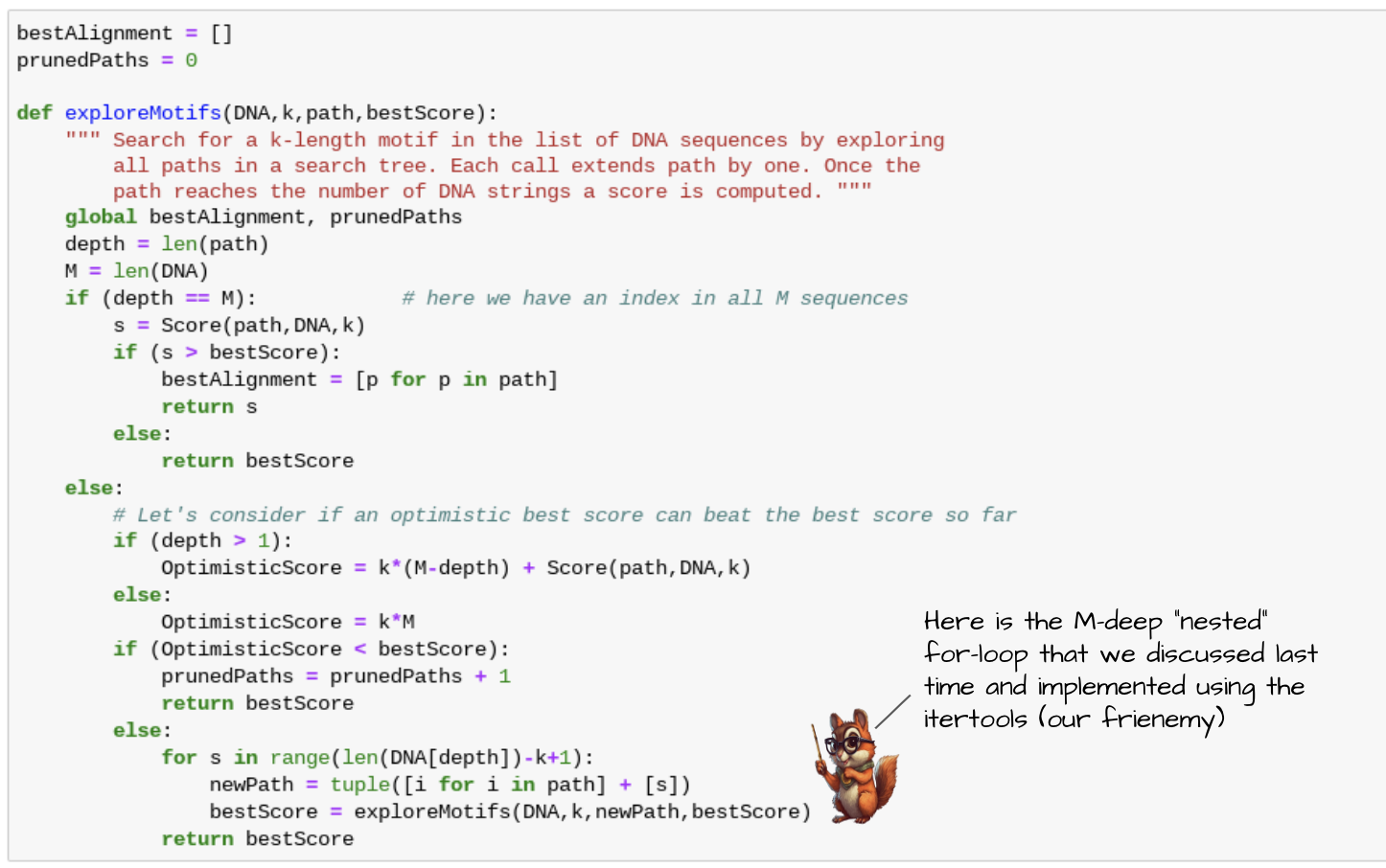
위에서 정리한 가지치기 알고리즘을 적용한 motif searching 알고리즘이다.
M개의 DNA 시퀀스에 대해 각 시퀀스를 살펴볼 때마다 깊이가 깊어지고, 깊이가 M이 되면 이때 점수를 계산한다.
깊이가 M이 아닐 때는 현재 깊이에서 얻을 수 있는 최적의 점수를 계산한다.
이때는 Score 함수에 전제 offset 이 아니라 현재 깊이까지 구성한 offset 조합만을 넘기도록 한다.
이렇게 계산한 최적해가 지금까지 구한 최고 점수를 넘을 수 없다면 굳이 더 해보지 않고 바로 bestScore를 반환한다.
만약 최고 점수를 넘길 가능성이 있다면 path 를 갱신하고 재귀적으로 함수를 호출한다.

브루트포스 방법을 사용했을 때 13분이 걸렸던 작업을 3분만에 끝냈으며, 861만가지 경로를 잘라낸 것을 알 수 있다.
가지치기 방법은 '평균' 실행시간을 낮추는데는 효과적이다.
하지만 만약 우리가 찾으려는 motif 가 모든 DNA에서 맨 뒤에 존재했다면 어떻게 될까?
그때는 기존의 방법과 비슷하게 많은 경우를 해봐야 할 것이다.
이런 특이한 케이스의 입력에 대해서도 효과적으로 동작하기 위해서 탐색 순서를 재귀를 통해 구성하는 것이 아니라 랜덤하게 구성하여 대처할 수 있다. (물론 이것도 운이 좋지 않다면 최악의 경우를 피해갈 수는 없을 것이다.)
Scanning-and-Scoring
Median String Motif Serach
기존의 접근 방법은 결국 모든 offset permutation 을 다 해보는 방법이었다.
만약 어떤 전지전능한 존재가 있어서 우리한테 motif 가 무엇인지 알려주었다고 해보자.
그러면 그 motif 를 M개의 DNA 에서 찾는 시간은 훨씬 적게 걸릴 것이다.
M개의 DNA 각각에 대해 N-k+1 개의 k-mer을 돌면서 hamming distance 를 계산하고, 그 최솟값을 취하면 되기 때문이다.
그리고 이렇게 M개 DNA 에 대해서 motif 위치를 찾아낼 수 있다.
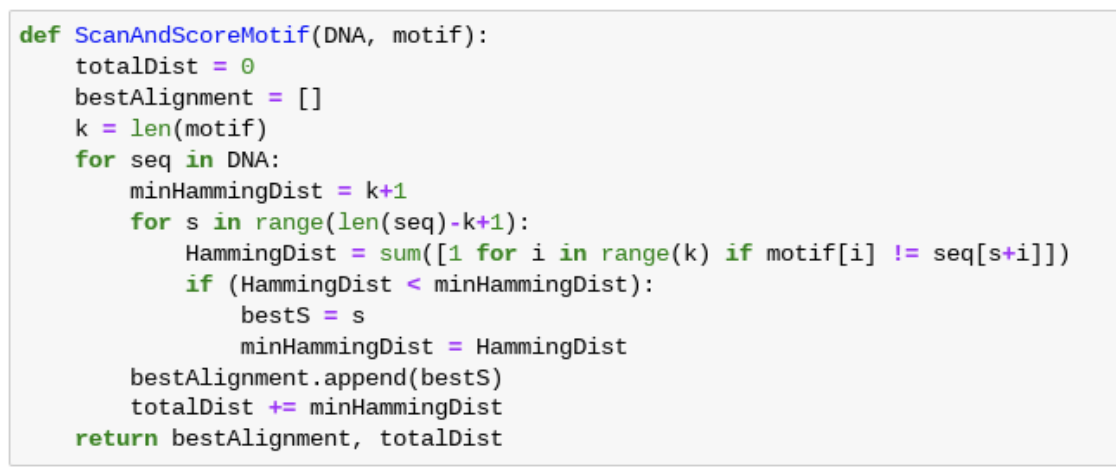
이를 코드로 구현한 것은 위와 같다.
DNA 에는 여러개의 DNA 문자열들이 존재한다.
각 문자열에 대해 hamming distance 가 최소가 되는 위치를 찾는다.
이때 초기값을 k+1 로 잡는 이유는 hamming distance 의 값은 0 ~ k 가 될 수 있기 때문에, k+1로 잡으면 매번 반드시 감소할 수 밖에 없기 때문이다.
하나의 문자열에 대해 minHamming Distance 를 구했다면, 그 거리를 구한 k-mer의 위치를 bestAlignment 배열에 추가하고, 그때의 거리를 totalDist 에 추가한다.

이 방법을 사용하면 M개의 DNA 시퀀스에 대해서, 각 시퀀스는 N-k+1 개의 k-mer을 갖고 있으므로 위와 같은 시간복잡도에 특정 motif에 대해 DNA 시퀀스들에서의 등장 위치를 찾을 수 있다.
이제 남은 것은 그 '특정 motif' 를 어떻게 결정할 것인지 고민해야한다.
만약 k-mer 에 대해서 특정 motif 를 모든 경우의 수로 시도해본다고 해보자.
(AAAAA...AAA 부터 TTTTT....TTTT 까지 다 해보기)
그러면 4**k 가지를 다 해봐야 할 것이다.
만약 k = 10 이라면 이 값은 100만가지 정도가 되며, 이 경우의 수에 대해 O(MNk) 시간복잡도를 갖는 점수 계산 알고리즘을 적용하면 대략 20분 내외의 시간이 걸린다.
이 방법도 시간이 걸리기는 하지만, 기존의 brute force 방법에 비하면 매우 빠르게 답을 구할 수 있다.
이런 방법을 Median String Motif Search 라고 부른다.
min hamming distance 를 찾는 것은 M개의 문자열들 사이의 거리를 그래프로 나타낼 때, 모든 문자열들과의 거리가 같은, 즉, 모든 문자열들의 가운데에 존재하는 문자열을 찾는 것과 같기 때문에 Median String 이라는 이름을 붙였다.
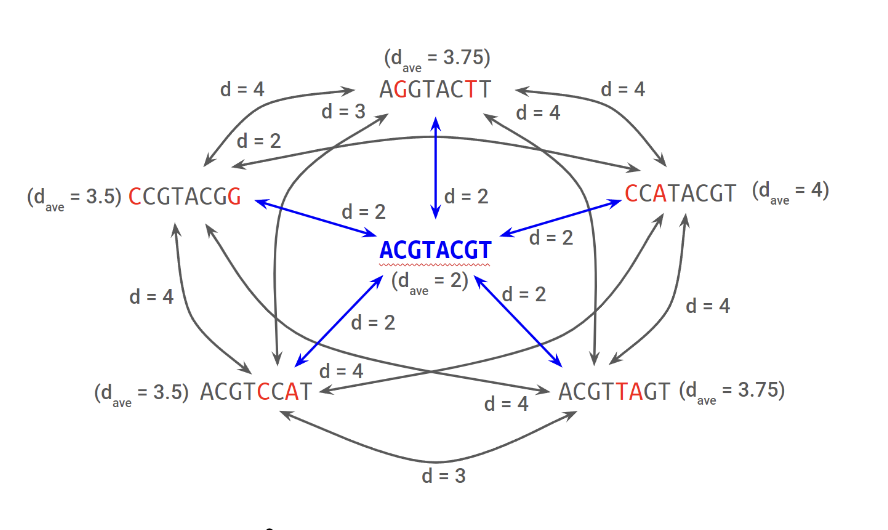
파란색 motif 문자열은 모든 문자열의 '가운데' 에 있다.

이를 코드로 구현하면 위와 같다.
기준이 될 motif 를 4**k 가지 다 만들고, 이 기준 motif 에 대해 ScanAndScoreMotif 함수를 매번 적용해서 최적해를 내뱉는 기준 motif 를 찾는다.
그리고 실행해보면 같은 답을 20분 정도의 시간에 빠르게 내는 것을 알 수 있다.
하지만 이 방법도 k 가 증가할 수록 점점 시간이 오래 걸린다.
(만약 k=20 이 되면 10**12 가지 경우의 수를 해봐야한다.)
따라서 여기에 대해서도 또 다시 가지치기 알고리즘을 적용할 수도 있다.
물론 가지치기 알고리즘은 '평균' 실행시간을 높여줄 뿐 최악의 경우에는 같은 시간이 걸린다는 것을 상기하자.
Contianed Consensus Motif Search
그렇다면 우리가 찾으려는 '특정 motif' 가 DNA 시퀀스에 포함되어있다고 가정하고 접근해보자.
그러면 4**k 이 아니라 (N-k+1)M 가지 k-mer 에 대해서 탐색을 해보면 될 것이다.
(물론 실제 정답은 k-mer 에 포함되어있지 않을 수 있지만, 일단 해보자.)

이 방법은 DNA 에 포함된 k-mer 들을 '특정 motif' 로 간주하고 min hamming distance 를 계산하는 기존의 방법을 적용한다.
그리고 이 방법을 통해 찾은 bestAlignment가 있다면, 여기에 대해 다시 기존의 Consensus 탐색 알고리즘을 적용한다.
(각 위치에서 가장 많이 등장한 문자를 Consensus의 각 문자로 취하기)

그러면 모든 DNA에서 나타날 수 있는 10-mer 중 적어도 하나는 반드시 10개의 후보 중에 존재한다.
그리고 이들에 대해 Consensus 을 정하는 알고리즘을 적용한다.
contained motif 와 consensus 를 비교해보면, 파란색 네모칸이 표시한 부분의 알파벳이 consensus 에서 바뀌면서 보정이 되는 모습을 볼 수 있다.
하지만 이 방법은 전체 가능한 해집합을 모두 탐색하지 않고, 그리디하게 최고 점수가 나오는 순간의 해만을 탐색하였으므로 100% 정답을 찾는다고 확신을 갖기 힘들다. 또한 이 방법을 사용하면 bias(편향)가 생기는 문제가 발생할 수도 있다.
Randomized Motif Search
이 문제를 해결하기 위해서 '특정 motif' 를 랜덤하게 취하는 방법을 사용할 수도 있다.

0부터 N-k+1 까지 수 중에서 하나를 고르는 과정을 M 번 반복한다.
그러면 임의의 offset permutation 하나가 나온다.
이 offset permutation 에 대해서 기존의 consensus 를 구하는 알고리즘을 적용한다.
그리고 이 consensus 를 우리가 사용할 '특정 motif' 로 사용한다.
이런 '특정 motif' 를 500번 반복하여 구해서 motif set 에 넣어두고, 이 motif 를 가지고 기존의 방법을 적용한다.

먼저 motifSet 을 복사한 testSet 을 만들어둔다.
그리고 testSet 이 비어있지 않을 때까지 다음을 반보갛ㄴ다.
새로운 비어있는 set 을 만든다.
그리고 testSet 을 돌면서 각 motif 를 기준으로 전체 DNA 에서 ScanAndScoreMotif 를 적용한다.
그러면 최소의 거리 합을 갖는 k-mer 위치들이 align 배열에 존재한다.
이제 이들에 대해 다시 Consensus 를 구하고, 이 새로운 motif 가 motifSet 에 존재하지 않는다면 비어있는 set에 넣는다.
또한 이때 구한 거리 합이 최소값을 갱신했다면 이 align 을 최적 align 으로 정한다.
과정을 마쳤다면 nextSet 을 testSet 으로 만들고, 기존의 motifSet 을 nextSet 과 합친다. (합집합)
이 과정을 거치면 점점 motifSet 의 크기는 점점 커질 것이고, 해볼 수 있는 다양한 consensus 를 다 해보게 된다.
(최초의 500개 motif 뿐만 아니라, 이에 대해 계산하면서 등장한 새로운 consensus 에 대해서도 다 해보는 것이다.)
이 알고리즘은 안정적인 답을 얻기 위해서 여러번 실행해봐야 한다.
'CS > 문제해결기법' 카테고리의 다른 글
| 6. Advanced Sequence Alignment (0) | 2024.10.29 |
|---|---|
| 5. Aligning Sequences (0) | 2024.10.29 |
| 3. Searching Pattern (0) | 2024.10.29 |
| 2. Genome (2) | 2024.10.28 |
| 1. Bioinformatics (1) | 2024.10.28 |
