지난 글까지는 여러개의 DNA 시퀀스에서 공통 motif (유사한 motif) 를 찾는 방법에 대해 정리하였다.
이번 글부터는 지난 글에서 찾아낸 각 DNA 염기 서열 속 motif 들 또는 전체 DNA 염기 서열이 얼마나 유사한지를 확인하기 위해, 정렬하는 방법에 대해 정리한다.

예를 들어, 위 문자열은 사람, 개, 고양이, 돼지의 인슐린 단백질의 아미노산 서열을 나타낸 모습이다.
이 서열은 얼마나 유사할까?

유사도를 측정하는 방법 중 하나는 각 문자열을 같은 문자끼리 '정렬' 하는 것이다.
위 모습은 4개의 인슐린 단백질 아미노산 염기 서열을 직접 손으로 정렬한 모습을 보여준다.
그리고 꽤나 긴 공통 서열이 나타나는 것을 알 수 있다.
그런데 이 공통 서열이 과연 우리가 찾을 수 있는 최적의 서열일까?
(사실 척추 동물의 인슐린 아미노산 서열은 거의 변하지 않아서 이건 쉬운 케이스이다.)
Alignment Game
먼저 간단하게 2개의 문자열을 정렬하는 방법을 일종의 '게임'으로 나타내보자.
목표 : 두 문자열에서 모든 문자를 제거하기
규칙 : 각 차례마다 3가지 행동 중 하나를 할 수 있다. 각 행동은 두 문자열 중 적어도 하나에서 문자를 지운다.
1. Match 버튼을 누르면 두 문자열에서 제일 왼쪽의 문자를 지운다.
만약 지운 두 문자가 같다면 1점을 얻고, 다르다면 0점을 얻는다.
2. Del 버튼을 누르면 윗 문자열에서 제일 왼쪽 문자를 지운다.
1점을 잃는다.
3. Ins 버튼을 누르면 아랫 문자열에서 제일 왼쪽 문자를 지운다.
1점을 잃는다.
과연 이 게임에서 높은 점수를 얻으려면 어떻게 해야할까?
브루트포스
정답을 찾기까지 버튼을 누르는 최소 횟수 = max( len(s1), len(s2) ) → match 누르고, 한쪽이 사라지면 del 이나 ins 누르기
정답을 찾기까지 버튼을 누르는 최대 횟수 = len(s1) + len(s2) → del, ins 만 누르기
따라서 모든 경우의 수는 3 ** (len(s1) + len(s2)) 보다 작다.
그런데 위의 상황에서 사람과 개의 인슐린 시퀀스 길이 합은 208이다.
3**208 = 1.73 x 10**90 으로 매우 큰 수다.
더 효율적인 방법이 없을까?
효율적인 풀이 방법
효율적인 풀이 방법을 알아보기에 앞서 맨하튼에서 최적의 관광 경로를 찾는 문제를 풀어보자.
MTP (Manhattan Tourist Problem)

맨하튼 관광 문제는 맨하튼 도시를 위와 같이 격자점으로 나타내고, * 로 관광지를 표시했을 때,
목적지를 향해서 움직이기만 하면서 (최단 경로로 이동하면서) 최대한 많은 관광지를 거치는 경로를 찾는 문제이다.

위 그래프에서는 각 경로에 적힌 숫자가 그 경로에서 볼 수 있는 관광요소의 개수를 말한다.
이 점수를 최대화해보자.
먼저 그리디 알고리즘을 적용해보면, 매 순간 가장 많은 관광요소를 볼 수 있는 길을 선택한다.
(빨간색 경로), 그 답은 18이며 최적이 아니다. (short horizon 방식)
이 방법을 개선하기 위해 다른 방법으로 접근해보자.
두 번째 방법은 현재 나의 위치에서 목적지 사이에 갈 수 있는 가능한 모든 엣지를 보고, 가능한 엣지 중에서 제일 많은 관광지를 볼 수 있는 엣지을 고른다. 이를 재귀적으로 적용한다.
예를 들어 source 에서 dest 사이에 제일 많은 관광지를 볼 수 있는 길은 '10' 이다.
이 10 이라는 길을 향해 최단 경로로 이동한다. (1 - 2 - 10)
이제 10 길을 따라 도착한 위치에서 목적지 사이에 존재하는 엣지 중에 제일 큰 엣지를 갖는 길을 고른다.
5가 2개가 있는데, 분홍색 경로를 따라서 5를 골랐다고 해보자.
그 길을 따라 도착한 곳에서 dest 까지 가는 경로는 유일하므로 이동한다.
이렇게 조금 더 넓게 보고 그리디를 적용한 long horizon 방식으로는 21의 답을 구했다.
이전보다는 나아졌지만 최적해인 22는 되지 않았다.
이번엔 DP를 이용해서 문제를 풀어보자.
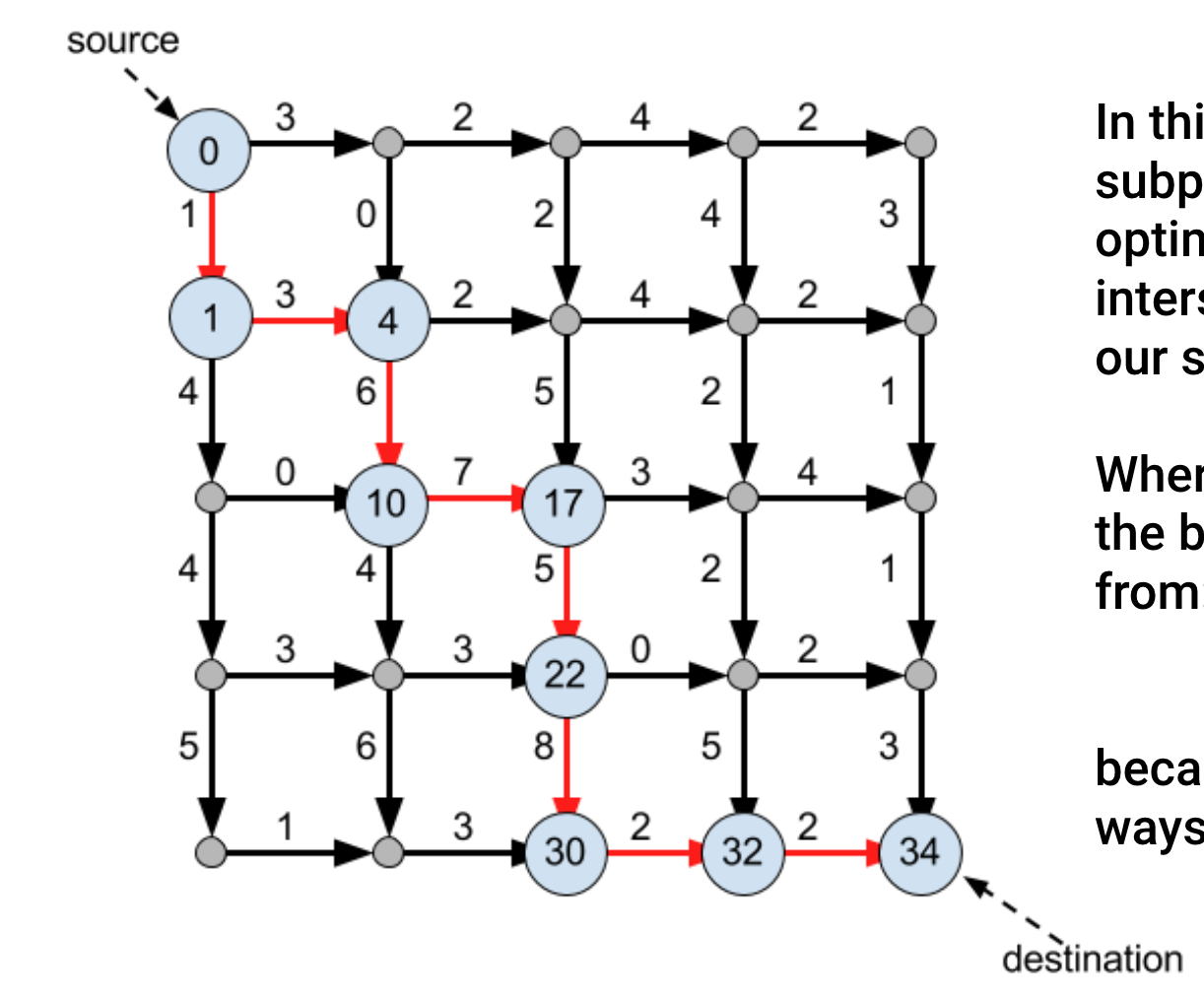
각 위치마다 현재 위치까지 도착했을 때 볼 수 있는 최대한 많은 관광지의 수를 기록한다.
이때 시작 위치에서 관광지의 수는 0이고, 이후에 이동할 때 그 위치의 관광지의 수는 (이 위치로 오는 경로에서 보는 관광지의 수 + 그 경로의 출발점이었던 위치까지 봤었던 관광지의 누적 수) 의 최댓값을 취한다.
예를 들어서, 2번째 기로줄, 2번째 세로줄 위치에 있는 '4' 라는 값은 그 위치로 오는 경로들에 대해 max(1 + 3, 3 + 0) = 4 를 통해 4로 결정된 것이다.
위와 같은 과정을 거쳐서 목적지에서의 관광지 수를 구하면 34로 최적의 관광지 수를 구할 수 있다.

이 말을 수학적으로 풀면 위와 같은 점화식을 사용한다.
이 방법으로 구한 해답은 '유일한 해답' 은 아닐 수 있다. (같은 개수의 관광지를 볼 수 있는 다른 경로가 존재할 수 있다.)
하지만 적어도 이 답이 '최적해' 임은 보장할 수 있다.
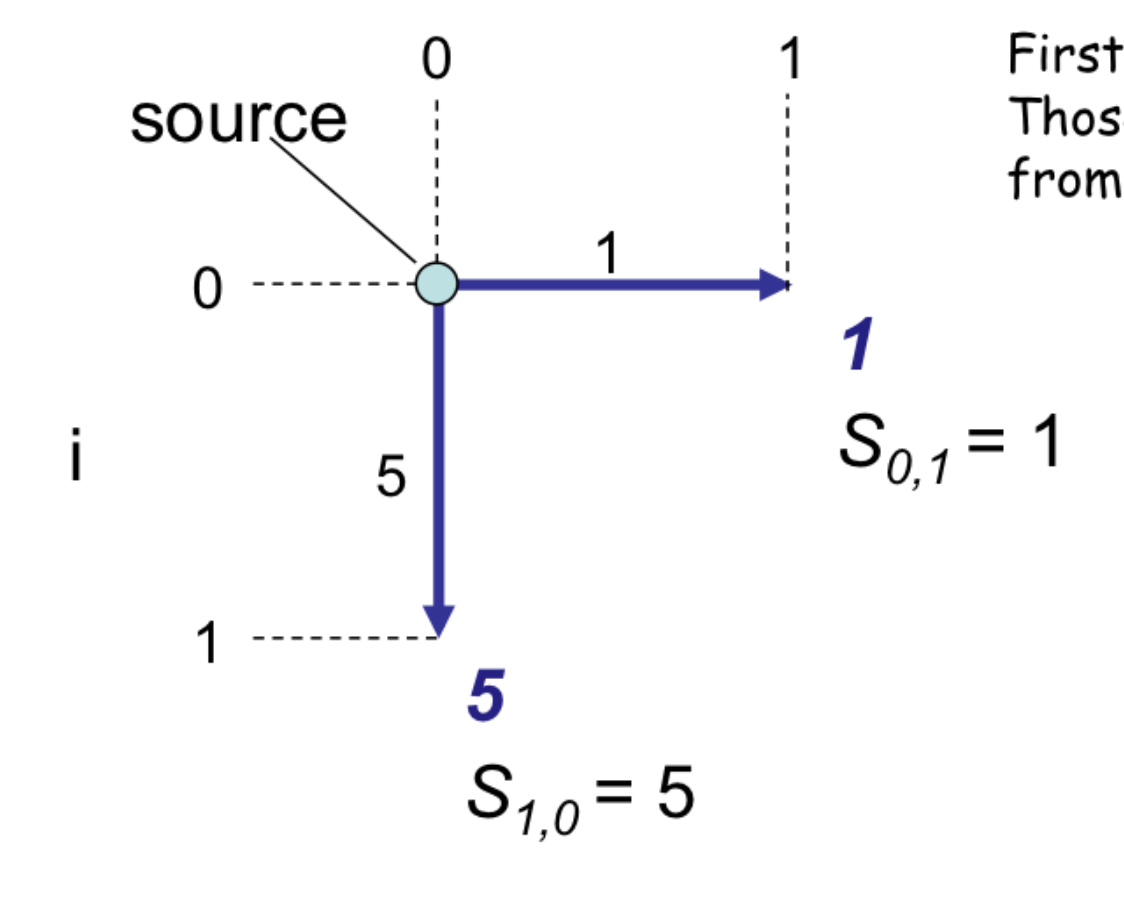
S 라는 score 2차원 배열을 채운다고 생각하면
S(1, 0) = 5, S(0, 1) = 1
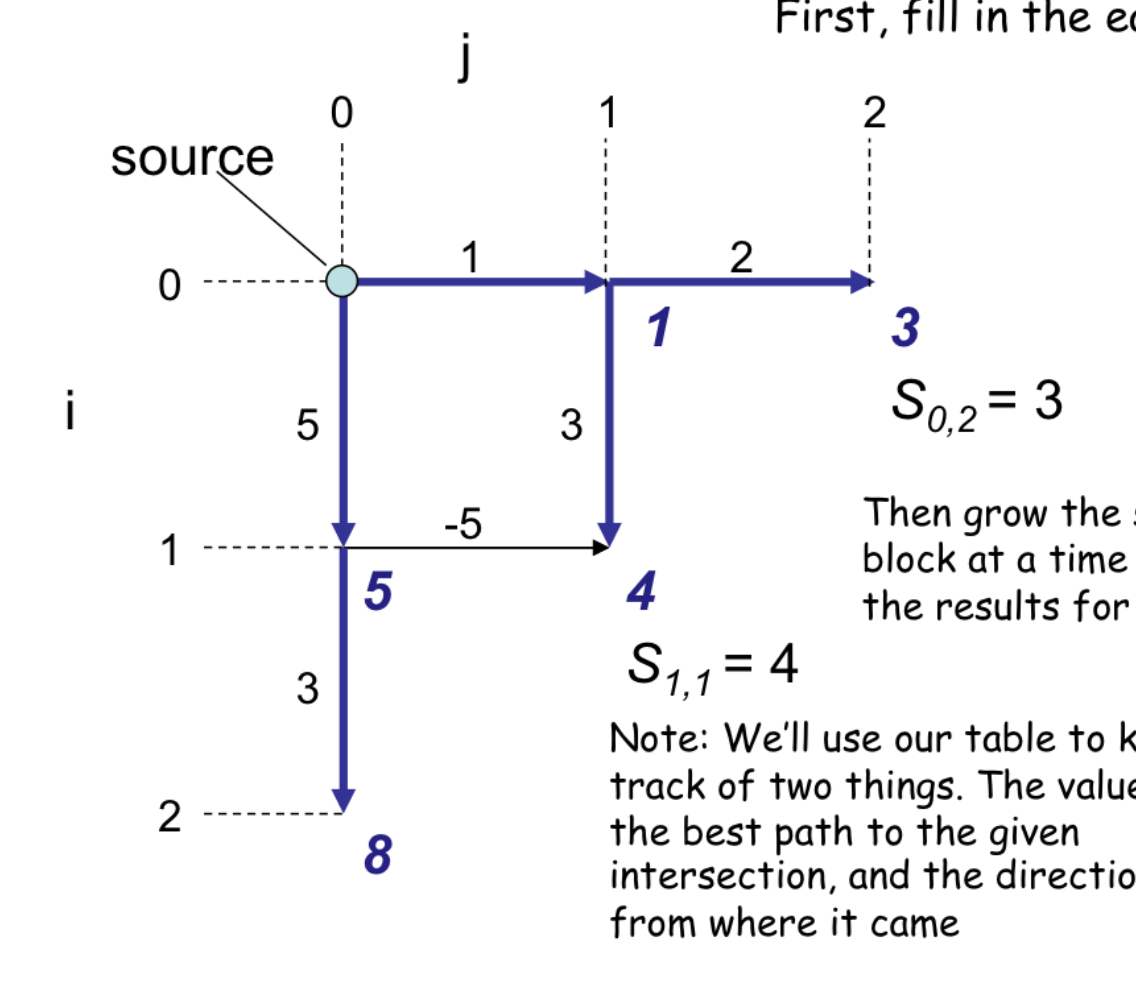
다음 단계에서는 이전 단계에 기록했떤 값을 활용하여 채운다.
S(2,0) = S(1,0) + 3 = 8
S(1, 1) = max(S(0,1) + -5, S(1, 0) + 3) = 4
S(0, 2) = S(0, 1) + 2 = 3
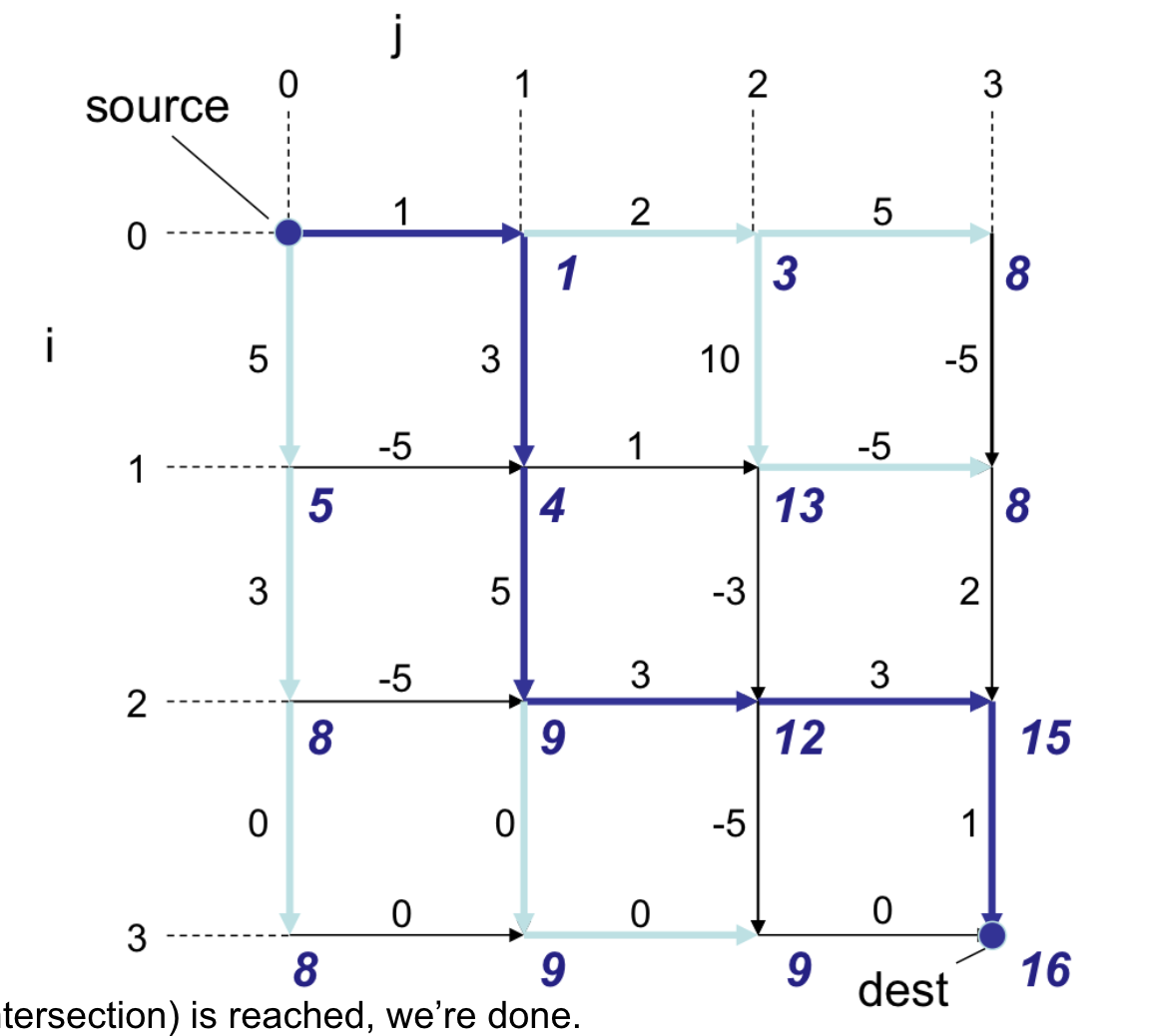
이런 과정을 반복하면 위와 같은 결과를 얻을 수 있으며, 백트래킹을 통해 경로를 찾을 수 있다.
이 최적해를 구하는 시간은 n x m 격자를 채우는 것과 같으므로 O(NM) 이다.
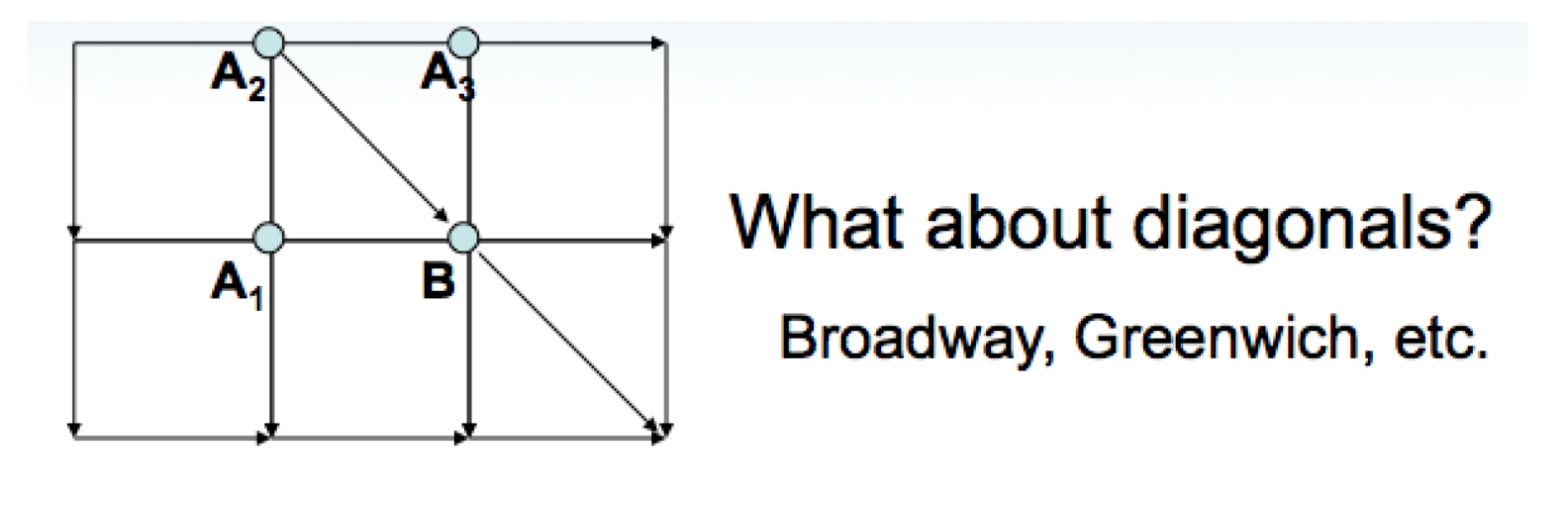
만약 격자판에 그림과 같이 대각선 경로가 있다면 어떨까?

그때는 점수를 계산하는 점화식을 이렇게 수정하면 된다.
이제 이 알고리즘을 기존의 DNA 서열 alignment 문제에 적용해보자.

두 문자열 v, w 의 hamming distance 를 구하면 6이다.
이 값은 꽤 큰 값이고, 따라서 두 문자열은 별로 비슷해보이지 않지만 만약 insertions, deletion을 적용하면 어떻게 될까?

이렇게 어떻게 insertion, deletion 을 적용하는지에 따라 기존보다 낮은 hamming distance 를 갖는 결과를 만들 수 있다.
(해밍 거리를 구할 때 insertion, deletion 은 무시한다. = 다른 것으로 취급한다.)
Edit Distance
1965년에 블라디미르 레븐슈타인은 edit distance 라는 개념을 제시했다.
이 개념은 두 문자열 사이에 insertion, deletion, substitution 을 적용하여 한 문자열을 다른 문자열로 바꾸는 최소 횟수를 나타낸다.
이 거리는 Hamming Distance 를 구하는 것보다 더 적은 연산으로 구할 수 있다.

예를 들어 TGCATAT 를 ATCCGAT 로 바꾸는 과정을 생각해보자.
1. TGCATAT 에서 맨 뒤의 T를 제거한다.
2. TGCATA 에서 맨 뒤의 A를 제거한다.
3. TGCAT 에서 맨 앞에 A를 삽입한다.
4. ATGCAT 에서 G를 C로 교체한다.
5. ATCCAT 에서 뒤의 A 앞에 G를 삽입한다.
ATCCGAT 완성
하지만 이것보다 더 적은 연산으로 문자열을 변환할 수 있다.

이는 최소값이며, edit distance 는 최소의 연산을 사용해야하므로, TGCATAT, ATCCGAT 사이의 edit distance = 4 이다.
또한 edit distance 는 교환법칙이 적용된다. 따라서 (w, v) 의 거리와 (v, w) 의 거리는 같다.
이는 deletion 과 insertion 이 상호보완적이라 그렇다.
따른 알고리즘에서는 이 두 연산을 합쳐서 INDEL 라고 부르기도 한다.
이 Edit Distance 의 변형으로, INDEL 만 허용하는 거리측정 방법이 있다.
이 방법은 LCS Distance 라고도 부르는데, LCS (Longest Common String) 부분 시퀀스는 꼭 연속적일 필요가 없고, 각 문자열에서 등장하는 순서만 같으면 된다.

예를 들어 위에서 LCS 는 HOISCOOL 이다.
LCS distance 는 LCS의 길이와 관련하여 다음과 같이 구한다.

위 예시에 대해서 LCS distance 를 계산하면

11 + 12 - 8 - 8 = 7 이다.
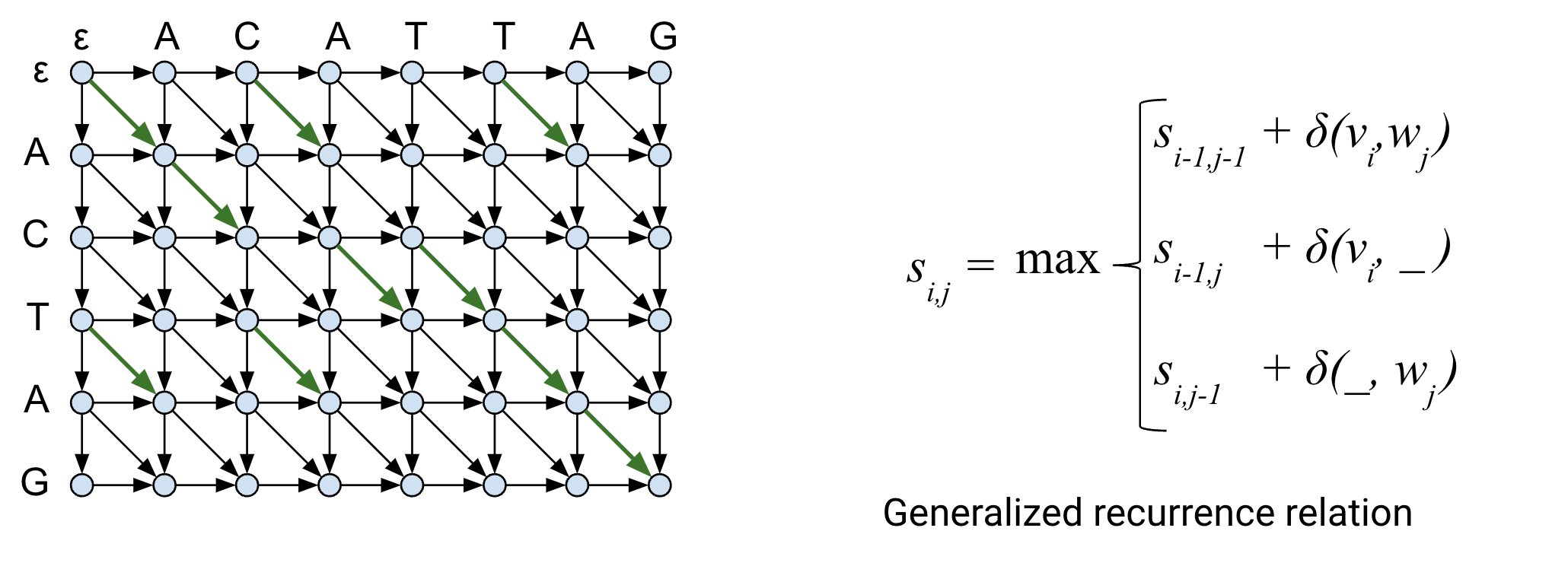
LCS와 MTP는 유사성이 있다.

이렇게 각 문자열을 하나의 축으로 하여 이차원 그래프를 만든다.
그리고 두 문자가 같아지도록 이동하는 경로에 대각선 경로를 만들고, 그 위치에 관광지 역할을 했던 * 표시를 남긴다.
이제 이 문제는 오른쪽 아래의 목적지로 이동하면서 최대한 많은 * 을 모으는 문제가 되었다.
가로로 가는 엣지는 v 에서 공백 ( _ ) 을 추가하게 되고, 세로로 가는 엣지는 w에 공백 ( _ ) 을 추가하게 된다.

위 문제에서 LCS는 위와 같다.
여기에서 대각선으로 이동하는 경우만 취하면 LCS를 구할 수 있고, 각 문자열에서 공백이 추가되는 위치는 가로/세로 간선의 이동을 보면 된다.

따라서 위와 같이 두 문자열을 정렬할 수 있다.
LCS distance 를 구하려면 LCS 의 길이를 구해야 한다.
따라서 대각선으로 이동할 때 점수를 매기고, 그 외 이동은 점수를 매기지 않도록 다음과 같은 점수 규칙을 적용한다.
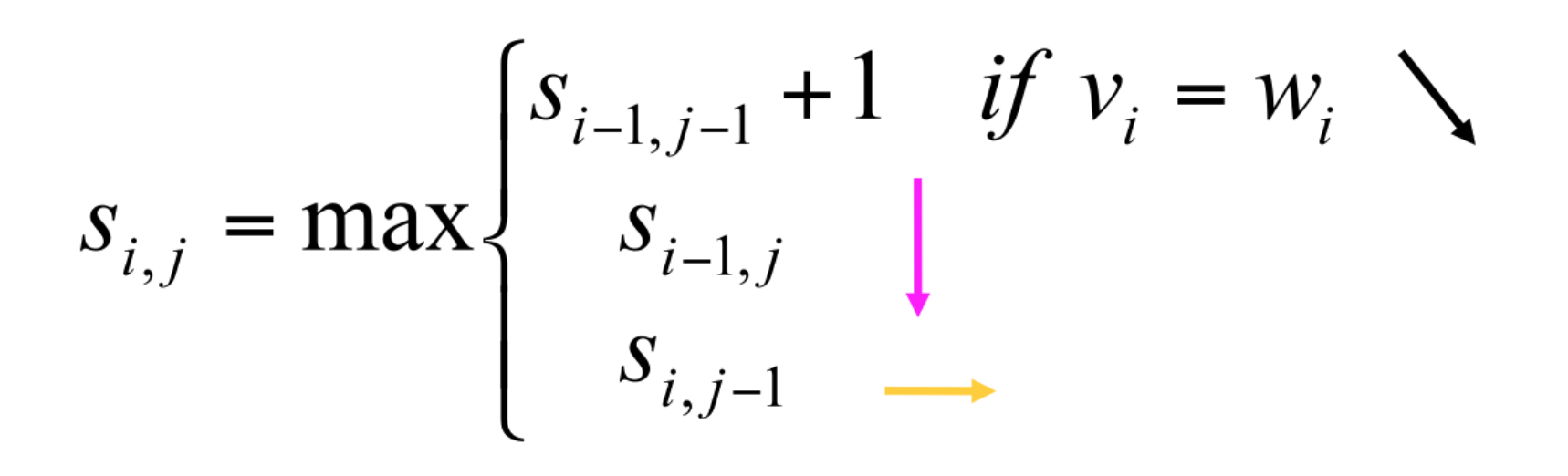
그리고 다음 점수판을 채운다.

처음에는 이렇게 0으로 초기화 되어있다.
이 점수판을 위 점수 규칙을 따라서 채운다.

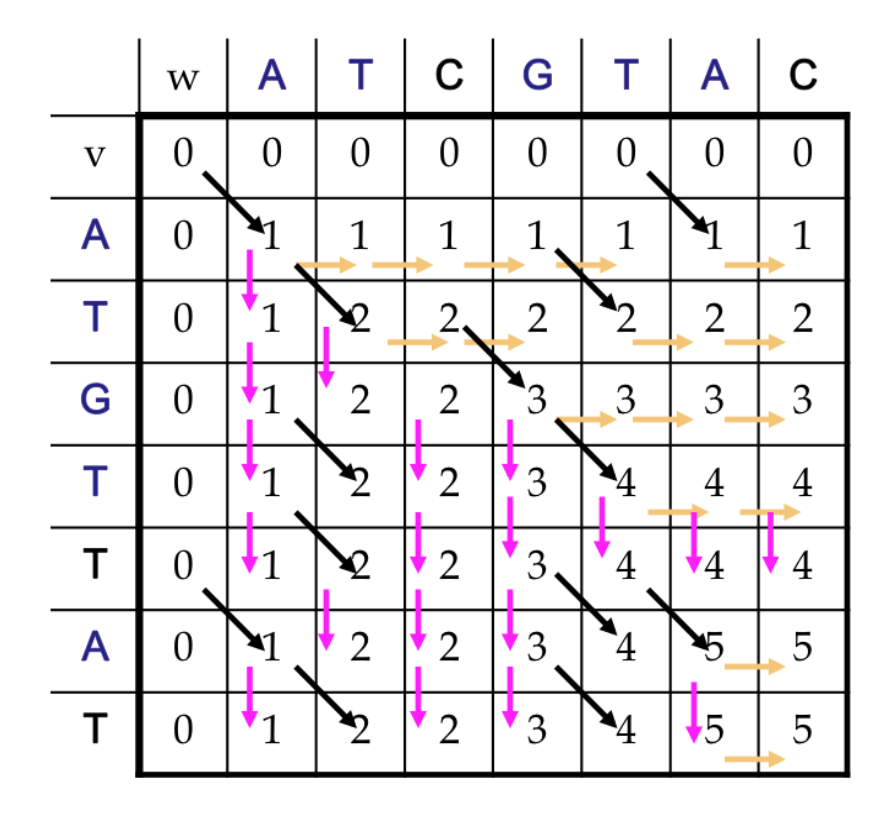
최종적으로는 위와 같이 점수판이 채워지며, LCS 길이는 5임을 알 수 있다.
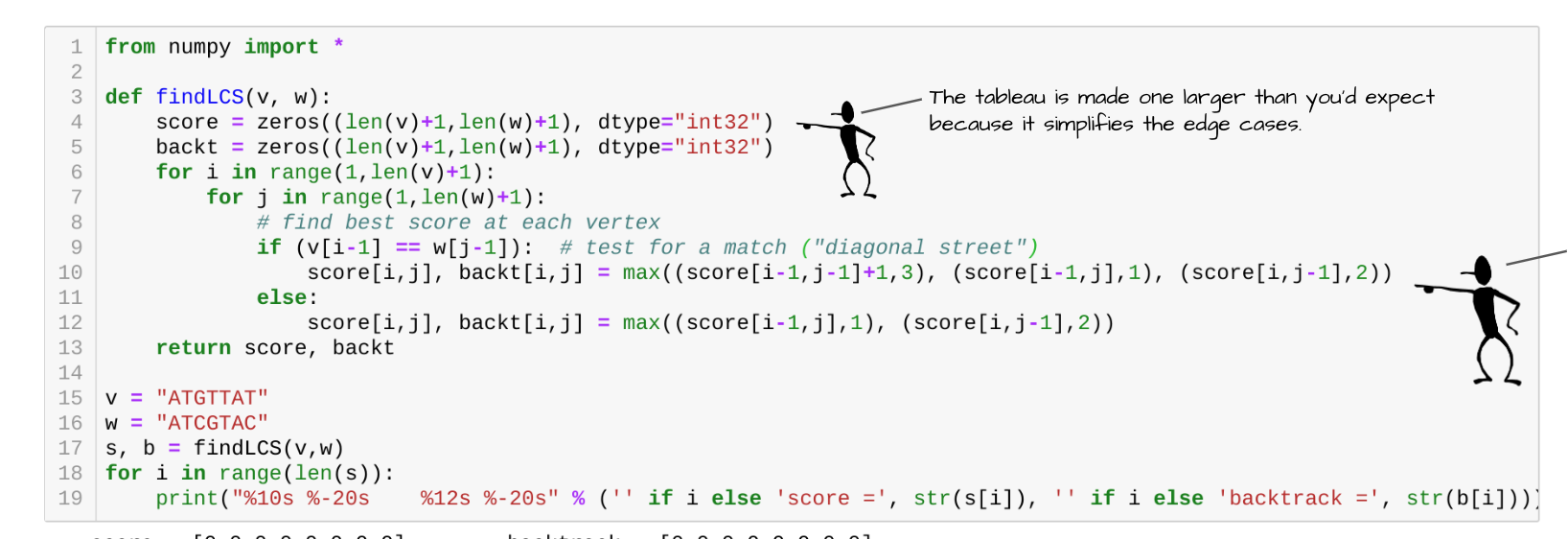
이를 코드로는 위와 같이 나타낼 수 있다.
2차원 리스트를 만들기 위해 numpy 를 사용한 코드이다.
이 코드를 사용하여 ATGTTAT, ATCGTAC 의 LCS를 구하면 다음과 같다.
이때 backtracking (경로 역추적) 을 위한 배열도 함께 채운다.
만약 현재 최고점수를 계산했을 때 (i-1,j-1) 에서 오는 것이 최고점이라면 3을 backt[i, j] 에 넣고
최고점수를 계산했을 때 (i-1, j) 에서 오는 것이 최고점이라면 2를, (i, j-1) 에서 오는 것이 최고점이라면 1을 backt[i, j] 에 넣는다.

실행결과는 위와 같다.
backtracking 배열로부터 실제 LCS를 찾을 때는 다음과 같은 코드를 사용한다.

오른쪽 아래에서부터 시작해서 3이면 왼쪽 위로 이동, 2이면 위로 이동, 1이면 왼쪽으로 이동하는식으로 옮겨가면서 LCS를 채운다.

그림으로는 위와 같다.
하지만 이건 LCS를 구한 것일 뿐이고, 아직 Alignment 는 하지 않았다.
Alignment 를 하려면 _ 를 적절히 추가해야 한다.

위 함수를 사용한다.
기존에는 백트래킹을 할 때 3만 고려해서 추가했다면 이번엔 1, 2 를 고려해서 v, w 를 동시에 구성한다.
이제 드디어 본론으로 돌아올 때가 되었다.
LCS 는 Alignment의 특별한 케이스였다.
이제 LCS distance 말고, Edit Distance 를 제대로 구해보자.

LCS와는 다른 점수 규칙을 사용한다.
LCS에서는 INDEL 만 허용했으므로, INDEL 을 할 때는 0점, 일치하면 1점 이었다.
이번엔 불일치를 허용하고, 일치하면 1점, 불일치하면 0점, INDEL 을 하면 -2로 패널티를 주었다.
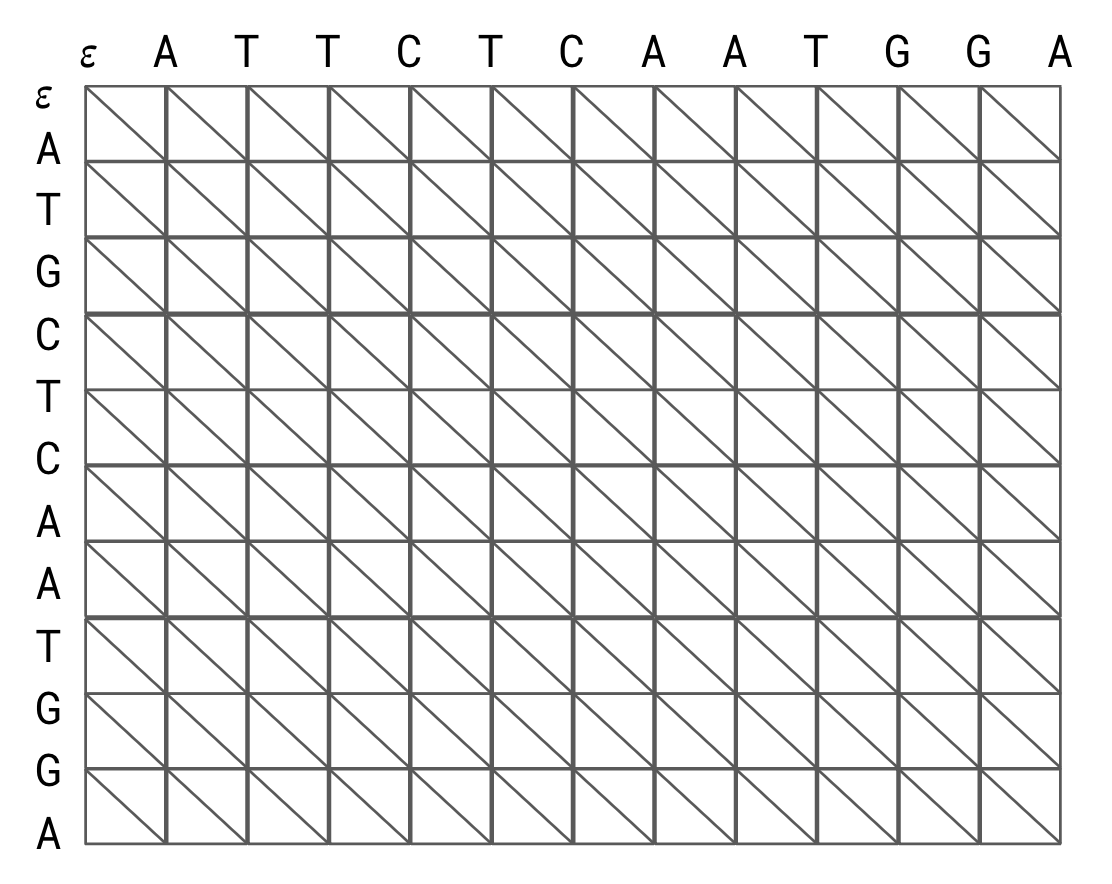
이번에는 위와 같이 그래프를 구성한다.
LCS 에서는 '일치할 때만' 대각선을 탈 수 있었지만, 이번인 불일치해도 대각선을 타고 내려갈 수 있기 때문에 모든 칸에 대각선이 존재한다.

이때 각 선택에 따른 비용을 측정할 때 동일한 비용을 사용하는 edit distance 대신, 별도의 score 행렬을 사용할 수도 있다.
A-G, T-C 는 상보적이므로 페널티를 적게 주고, 상보적이 아닌 염기 서열에는 페널티를 크게 준다.
또한 삽입/삭제는 교체보다 발생 빈도가 낮으므로 페널티를 더 크게 (-3) 준다.
이 점수 매트릭스를 사용해서 최적해를 찾아보자.
이렇게 찾은 최적해는 Global Alignment 에 해당한다.

이를 가리켜 Global 이라고 부르는 이유는 각 시퀀스를 구성하는 모든 문자가 최종 점수를 계산하는데 참여하기 때문이다.
반면 Local Alignment 도 존재한다.
Local Alignment 는 똑같이 최고 점수를 찾는 것이 목적이지만 (0, 0) 부터 (n, m) 까지 전체에 대해서 찾는 것이 아니라, (i, j) ~ (i', j') 까지 부분 문자열에 대해서 최고 점수를 찾는다.

위 그림은 두 정렬 방법의 차이를 보여준다.
서로 다른 두 종에 존재하는 두 유전자는 짧은 부분에서 비슷하고, 나머지 영역에서는 비슷하지 않을 수 있다.
이런 경우에는 Local Alignment를 통해 유사성을 측정하는 것이 더 좋다.
Local Alignemnt 는 두 문자열의 모든 가능한 부분 문자열 조합 중 가장 높은 점수를 내는 부분 문자열을 찾는 것이 목표이다.
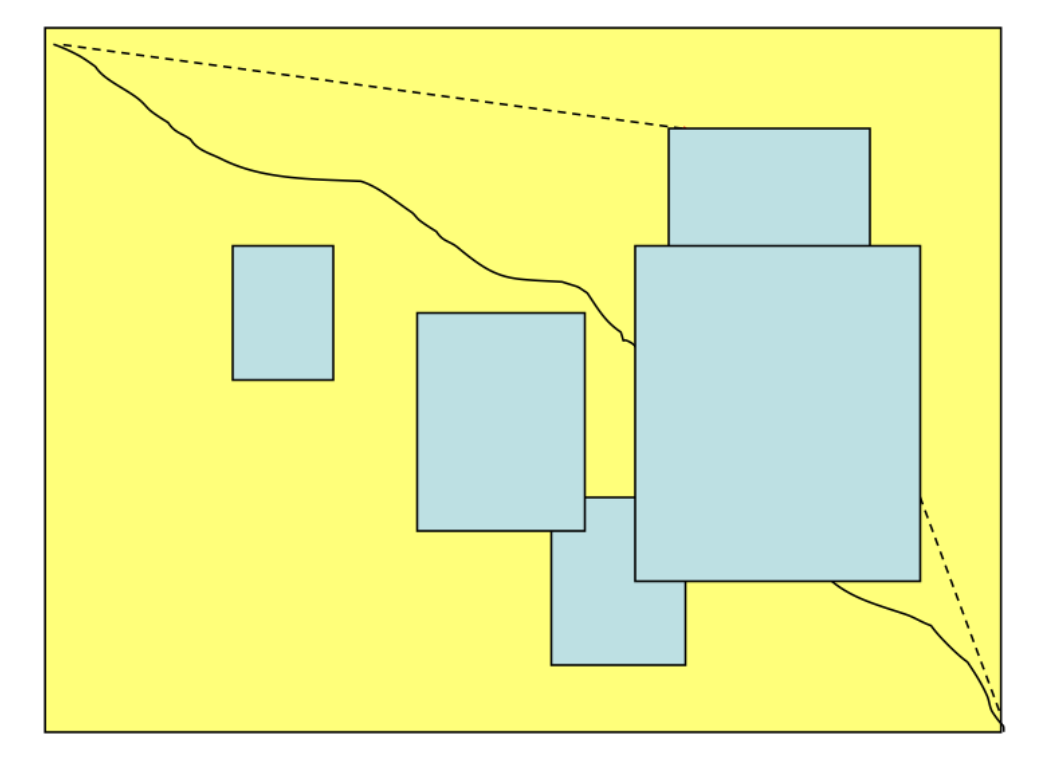
Local Alignment 를 구하는 첫 번째로 가능한 경우는 가능한 사각형 영역을 다 구해보는 것이다.
왼쪽 위 좌표와 오른쪽 아래 좌표 각 2개씩을 모두 선정하는데 N**2, 하나의 사각형 안에서 Local Alignment 를 찾는데 N**2 해서,
총 O(N**4) 시간 복잡도가 걸린다.
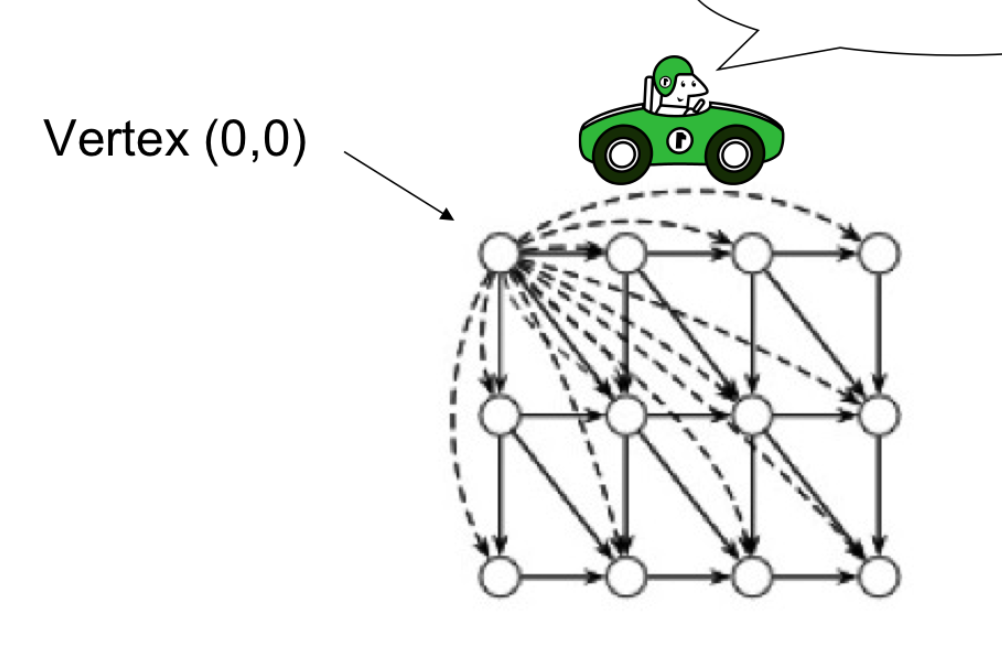
더 빠르게 구하기 위해 Free Rides 라는 방법을 사용할 수 있다.
이 방법은 (0, 0) 위치의 노드에서 다른 노드로 한번에 갈 수 있는 모든 edge 를 추가한다.
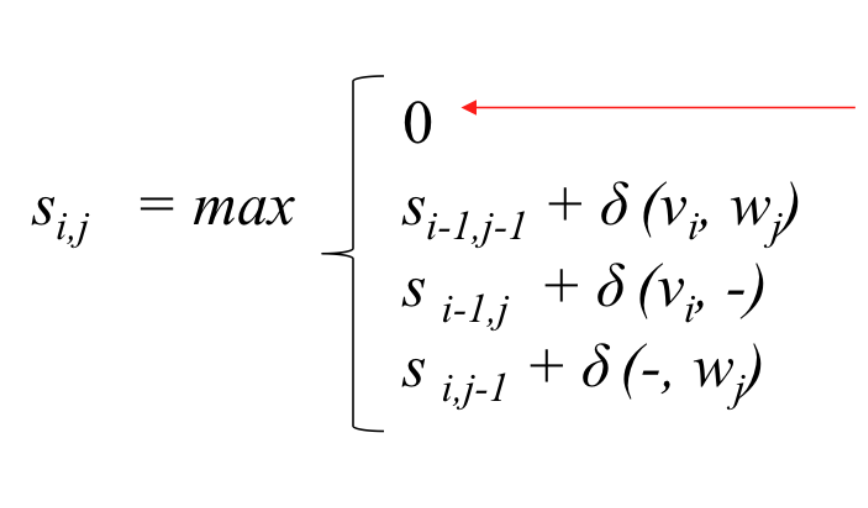
그리고 점수를 구하는 방법을 위와 같이 수정한다.
0을 선택하는 경우는 local alignment 를 위해 시작점을 이동할 때 사용한다.
(점수를 계산할 때 음수가 나오면 그 위치에서는 그냥 점수를 0으로 설정하고 거기서부터 새로 계산을 시작한다.)

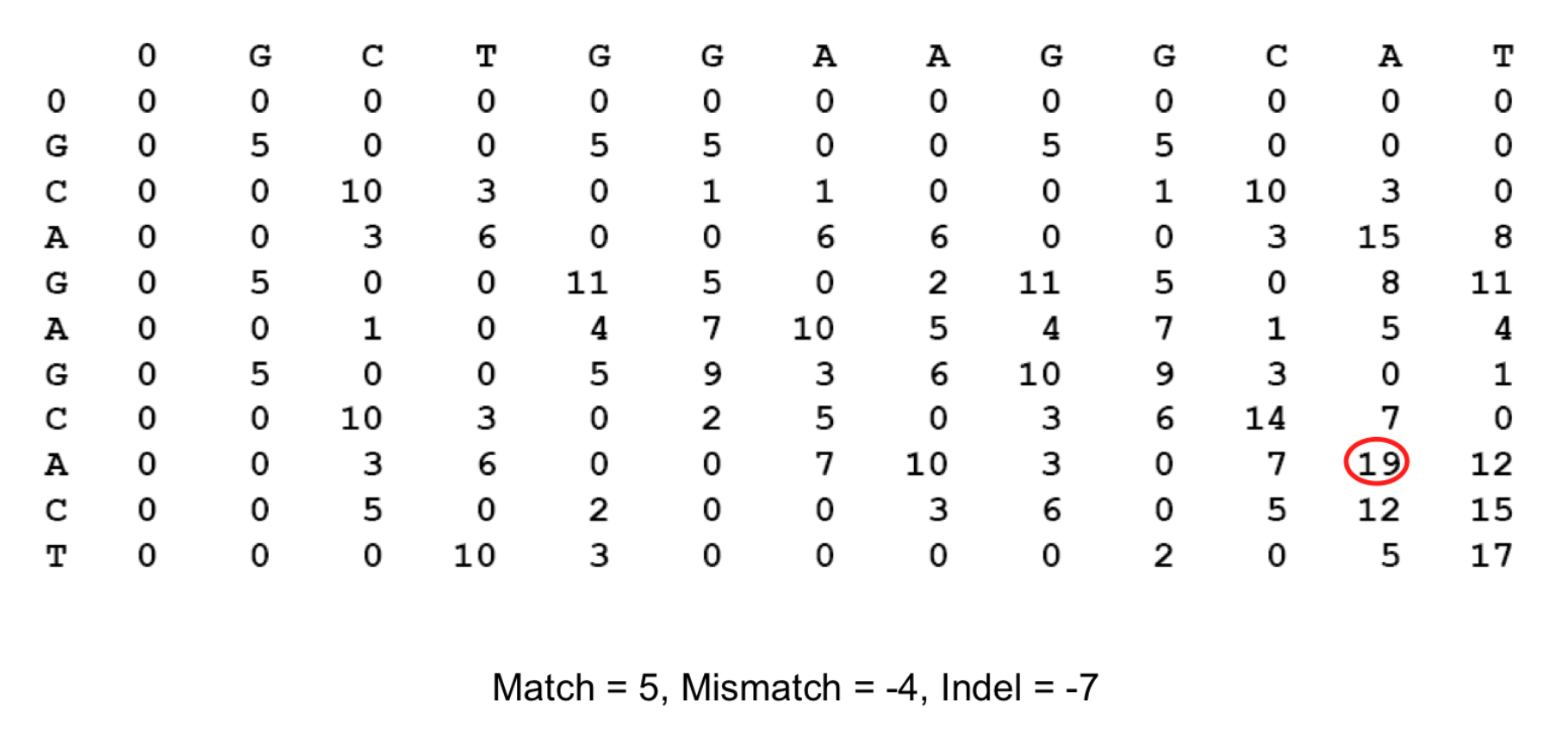
최적해가 19이므로, 19가 나오도록 만들었던 local alignment 를 찾는다.
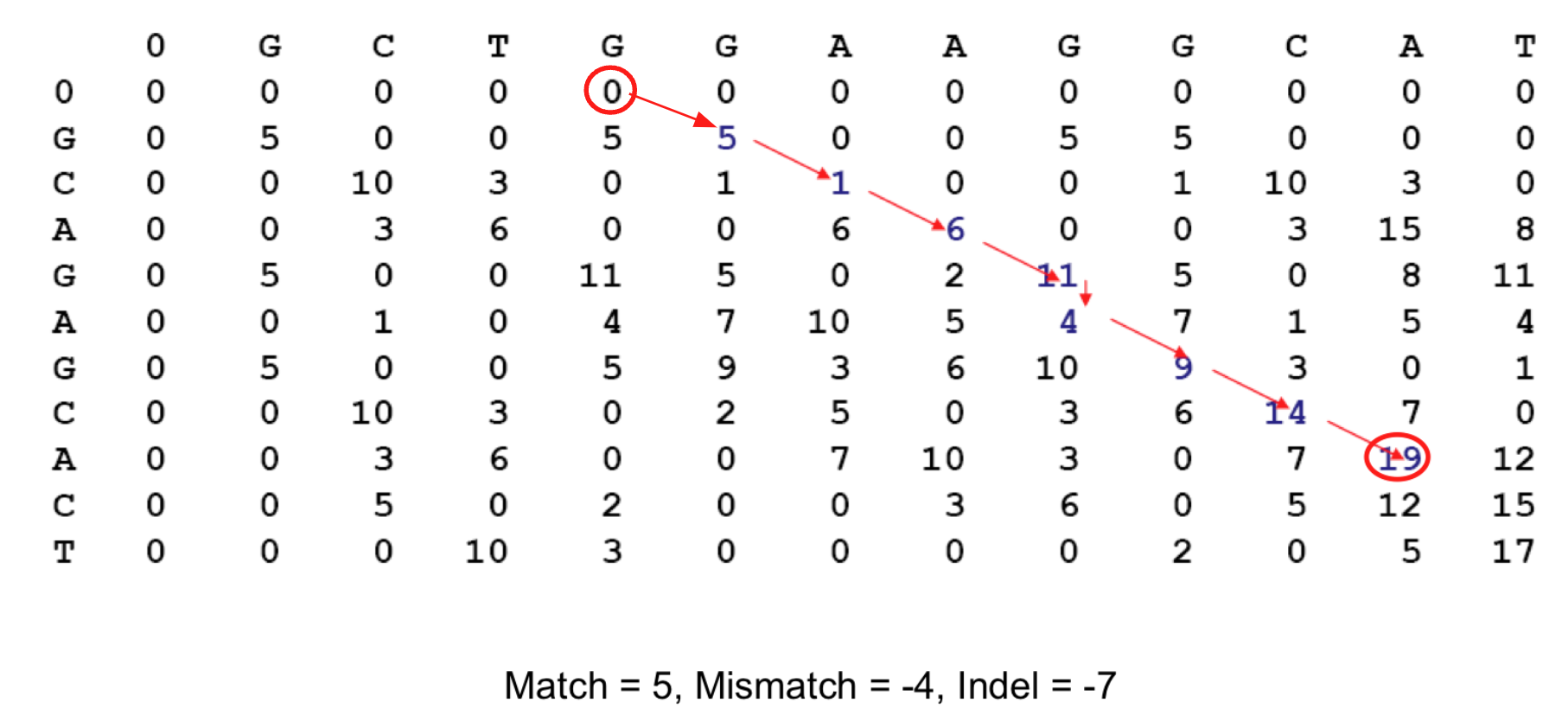
0을 만날 때까지 백트래킹을 진행한다.
만약 Global Alignment 였다면 (0, 0) 까지 백트래킹을 진행했을 것이다.
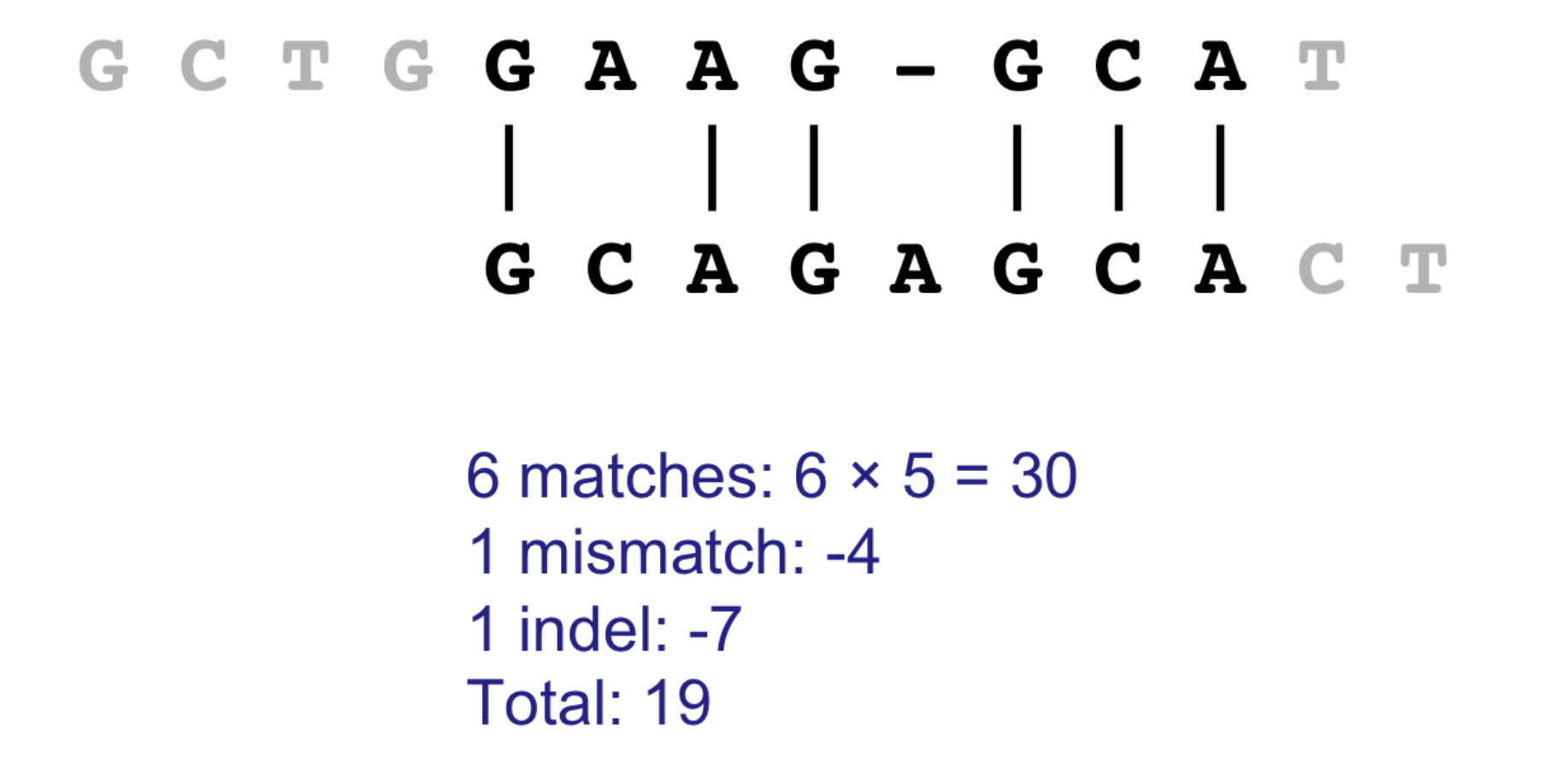
위 그림에서 19점이 계산된 것은 위와 같은 Alignment 가 발생한 것과 같다.

Global Alignment 를 해보면 8점이 나오는 것을 알 수 있다.
훨씬 더 적은 점수가 나온다.

위 그림 상황에 맞는 Local Alignment 를 코드로 구현한 것은 위와 같다.
INDEL 에서는 -7점, mismatch 는 -4 점, match = 5 점의 점수를 부여한다.

백트래킹은 위와 같이 작성할 수 있다.
GlobalAlignment 와 다른 점은 재귀 함수의 종료조건이다.
기존에는 (0, 0) 에서 멈추었지만, 이번에는 backtracking 행렬의 값이 0이면 멈춘다.
'CS > 문제해결기법' 카테고리의 다른 글
| 7. Assembling a Genome (0) | 2024.10.30 |
|---|---|
| 6. Advanced Sequence Alignment (0) | 2024.10.29 |
| 4. Finding TFBS Motifs in our lifetime (0) | 2024.10.29 |
| 3. Searching Pattern (0) | 2024.10.29 |
| 2. Genome (2) | 2024.10.28 |
