해시 기반 인덱스
해시 기반 인덱스는 등호 조건 조회에 최적화된 인덱스 기법이다.
(범위 조건 조회에는 사용할 수 없다. 탐색 키가 <a, b, c> 일 때, a >= 10 과 같은 질의를 수행하려면 10, 11, 12, .. 를 모두 해싱해야 하며, a = 10 에 대해서도 b, c 를 임의의 값을 모두 지정해서 해싱해야 하기 때문이다.
반면 a = 1, b = 2, c = 3 과 같이 조건이 명확할 때는 매우 빠르게 원하는 데이터를 찾아낼 수 있다.
정적 해싱
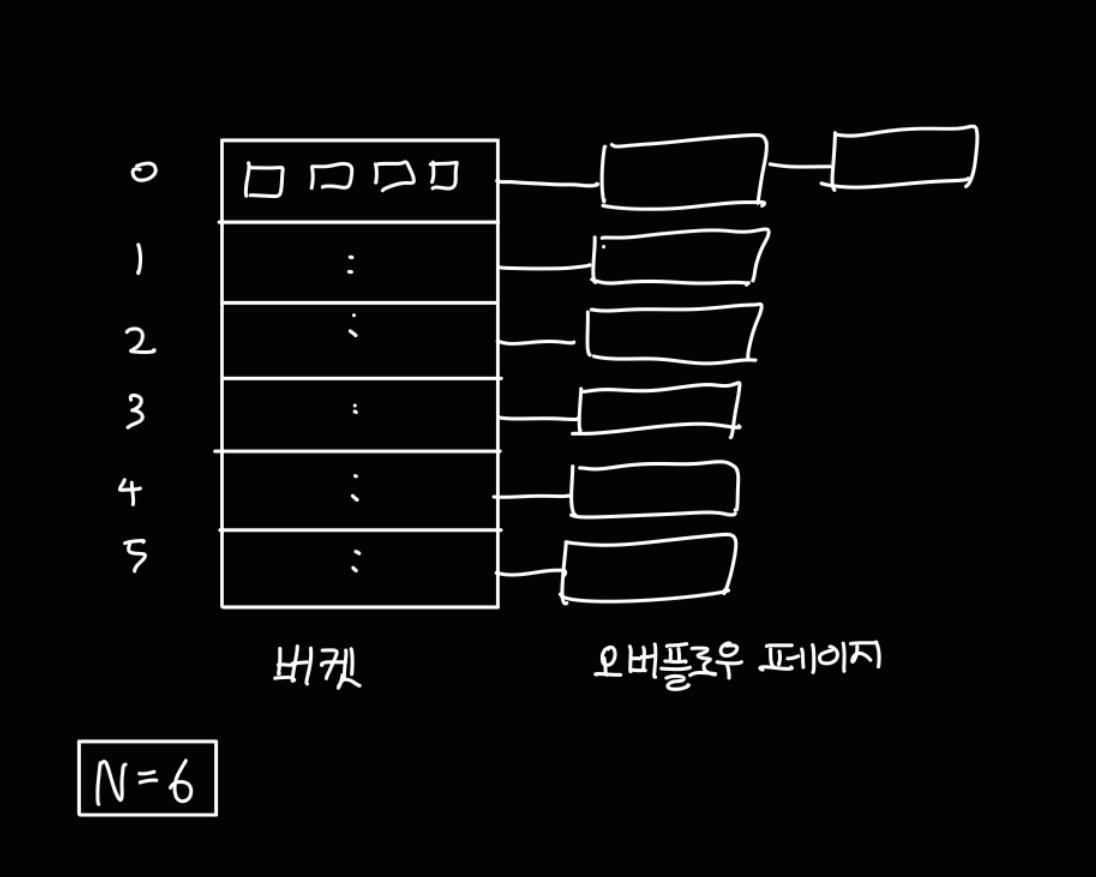
정적 해싱 기반의 인덱스는 primary bucket page 와 overflow page 로 구성된다.
하나의 인덱스 파일은 0 ~ N-1 까지의 고정된 크기의 버켓으로 이루어지며, 처음에는 버켓 당 하나의 기본 페이지만 존재한다.
버켓은 데이터 엔트리를 갖고 있고, 데이터 엔트리를 탐색할 때는 해시함수 h 를 사용하여 h(search key) % N 연산 결과를 통해 버켓을 찾아 데이터 엔트리를 찾는다.
만약 새로운 데이터를 추가하려고 하는데, 해싱 결과 해당 버킷 페이지에 이미 데이터 엔트리를 추가할 공간이 없다면 overflow page를 만들어 저장한 뒤 해당 버킷 페이지의 오버플로우 체인에 연결한다.
이 과정이 반복되면 시간이 지났을 때 거의 선형 탐색하는 것과 다를 바 없는 시간이 소모되므로, 동적으로 이를 조정하는 기법이 필요해졌다.
확장성 해싱 (Extendible Hashing)
해시 충돌이 발생하여 동적으로 버킷 크기를 늘리는 상황이라고 생각해보자.
만약 그냥 버킷 크기를 임의로 늘린다면, 버킷 크기가 늘어남에 따라 모든 데이터에 대해 늘어난 버킷 크기에 대해 저장 공간을 재배치해야 하는 문제가 발생한다.
(N = 6 에서 N = 8로 늘린다면, 나머지가 6, 7 인 데이터를 기존의 나머지 0, 1 위치에서 6, 7 위치로 옮겨야 한다.)
따라서 데이터의 재배치를 최소화하는 기법으로 확장성 해싱이 등장했다.
확장성 해싱은 해시 충돌이 발생하면 충돌이 발생한 그 번호에 대해서만 버킷을 쪼개는 방식으로 데이터 엔트리를 저장하며, 오버플로우 페이지는 생기지 않는다. (단, 데이터가 '중복' 되는 경우에는 오버플로우 페이지가 필요할 수 있다.)

확장성 해시에는 실제 데이터 엔트리를 저장하는 데이터 페이지와, 데이터 페이지 주소를 가리키는 배열인 디렉토리로 구성된다.
디렉토리에는 Global Depth, 각각의 데이터 페이지에는 Local Depth 가 있는데, Global Depth 는 디렉토리의 모든 레코드를 식별하는데 필요한 비트 수, Local Depth 는 해당 페이지를 식별하는데 필요한 비트 수를 나타낸다.
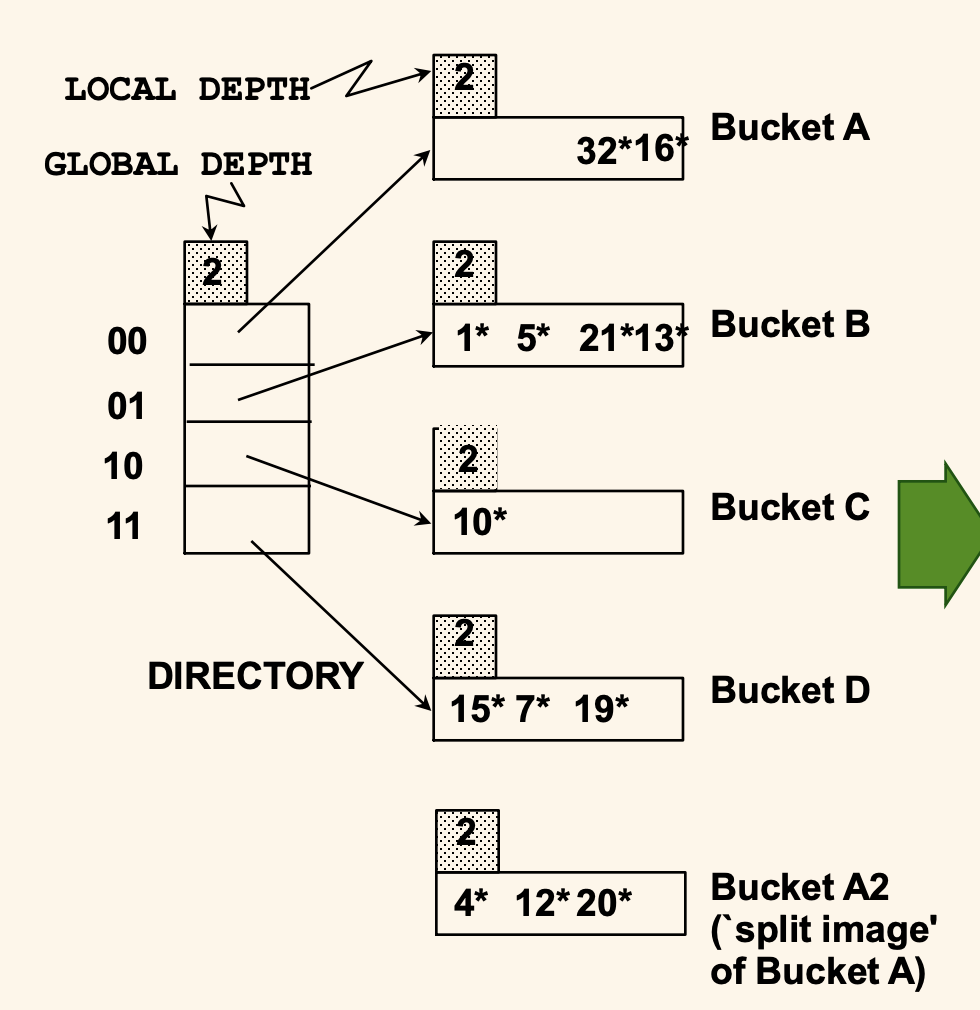
위 그림은 Global Depth, Local Depth 가 모두 2인 초기 상태를 보여주며, 데이터 엔트리는 위와 같이 저장되어있다.
각 데이터 페이지에는 최대 4개의 데이터 엔트리가 저장될 수 있다.
Global Depth 가 2라는 뜻은 디렉토리 배열의 크기가 2^2 = 4 이며, 각각을 식별하는데 필요한 비트의 수가 2라는 것을 나타낸다.
00 디렉토리는 2^2 = 4로 나눈 나머지가 0인 데이터 엔트리를 저장하는 페이지를 가리키며 해당 데이터 페이지에는 4, 12, 32, 16 이 들어있다.
01 디렉토리는 4로 나눈 나머지가 1인 데이터 엔트리를 저장하는 데이터 페이지를, 10 디렉토리는 나머지가 2, 11 디렉토리는 나머지가 3인 데이터 엔트리를 저장하는 데이터 페이지를 가리킨다.
여기에서 새롭게 20 이라는 데이터 엔트리를 추가한다고 해보자.
20을 이진수로 나타내면 최하위 2비트는 00 이므로 00 디렉토리가 가리키는 데이터 페이지에 데이터를 저장하려고 한다.
그러나 해당 데이터 페이지에는 데이터 엔트리가 가득 찬 상황이다.
이런 경우에, 확장성 해싱은 디렉토리의 크기를 2배로 늘리고, 데이터 엔트리가 가득찬 데이터 페이지의 데이터 엔트리를 재정렬한다.
엔트리를 재정렬하는 방법은 간단하다.
페이지를 식별하는데 필요한 비트 수를 1개 더 늘리면 된다.
따라서 3개 비트를 가지고 데이터 엔트리를 분류하기 위해, Local Depth 를 1 증가시키고 다음과 같이 데이터를 분류한다.
4, 12, 20 은 모두 100 으로 끝나는 데이터 엔트리, 32, 16은 모두 000 으로 끝나는 데이터 엔트리이다.
(위 그림에서는 아직 Local Depth 가 증가하지 않은 상태이다.)
그리고 이렇게 버켓을 나누어 데이터 엔트리를 재분류 한 뒤, 디렉토리가 각각의 버켓을 가리킬 수 있도록 디렉토리의 크기를 2배로 늘린다.
디렉토리의 크기를 2배로 늘리는 것 역시, 데이터 페이지를 식별하는데 사용할 비트 수를 1개 더 사용한다는 뜻과 같으며 Global Depth 를 1 증가시키는 것과 같다.

Global Depth 가 증가하면, 위 그림과 같이 디렉토리의 크기가 8로 증가하며, 각각을 식별하는데 3개의 비트를 사용한다.
(즉, 해시 함수의 결과 값이 3비트로 증가한다는 것과 같다.)
아직 Local Depth 가 2인 데이터 페이지를 식별할 때는 디렉토리에서 하위 2비트가 같은 칸이 같은 데이터 페이지를 가리키도록 하고, 쪼개진 A, A2 는 각각 000, 100 이 가리키도록 포인터를 나눔으로써 오버플로우 페이지 없이 데이터를 저장할 수 있다.
이때 헷갈리지 않도록 주의할 점은, 버켓을 쪼갤 때 항상 디렉토리의 크기가 2배로 증가하지는 않는다.
(splitting a bucket does not always require doubling.)
예를 들어 Bucket B 에 새로운 데이터가 들어와서 버켓을 2개로 쪼개더라도, 기존의 디렉토리 공간에서 충분히 포인터를 나눠서 새로운 버켓을 가리킬 수 있으므로 디렉토리를 두배로 늘릴 필요가 없다.
(쉽게 정리하면, Local Depth 가 Global Depth 를 넘지 않는 한, Global Depth 가 증가할 필요는 없다.)
다시 정리하면, Global Depth 는 버켓을 식별하는데 필요한 '최대' 비트 수
Local Depth 는 특정 데이터 엔트리가 속할 버켓을 결정하는데 필요한 '실제' 비트 수를 말한다.
선형 해싱 (Linear Hashing)
선형 해싱은 확장성 해싱의 대안 방법으로, 디렉토리대신 여러 개의 해싱 함수들을 사용하여 중복 데이터를 관리한다.
초기에 사용하는 해싱 함수 h₀ 는 초기 버켓의 개수 N 과 같은 가짓수의 결과를 내보낸다.
만약 N = 32 라면, h₀ 의 적용 결과는 0 ~ 31 사이의 값이 나올 수 있다.
그 다음의 해시 함수 h₁ 는 2N 가지의 결과를 내보내는 0 ~ 63 사이의 값을 내보내고,
그 다음의 해시 함수 h₂ 는 4N 가지의 결과를 내보내는 0 ~127 사이의 값을 내보낸다.
이를 일반화하면 아래와 같이 작성할 수 있다.
hᵢ(key) = h(key) % (2ⁱN)
이때 hᵢ 와 h 는 서로 다른 해시 함수이며, h는 0~N-1 사이의 값을 만들어낼 필요는 없다.
어차피 모듈러 연산을 취할 것이기 때문이다.
이제 이 해시 함수들을 사용하면 어떻게 인덱스로부터 데이터를 빠르게 찾을 수 있는지 알아보자.
먼저 현재 라운드를 나타내는 변수를 Level = 0 으로 초기화해둔다.
다음에 분할될 버켓은 Next 변수로 가리키며, 처음에는 Next = 0 으로 첫번째 버킷을 가리킨다.
Level 번째 라운드의 시작에, 파일에 존재하는 버켓의 수는 N_Level 로 표현한다.
그러면 N_Level = N * 2^Level 이다. (Level 이 증가할 때마다 N이 두 배씩 늘어난다.)
Level = 0 일 때 버켓의 수 N₀ = 4 라고 하자.
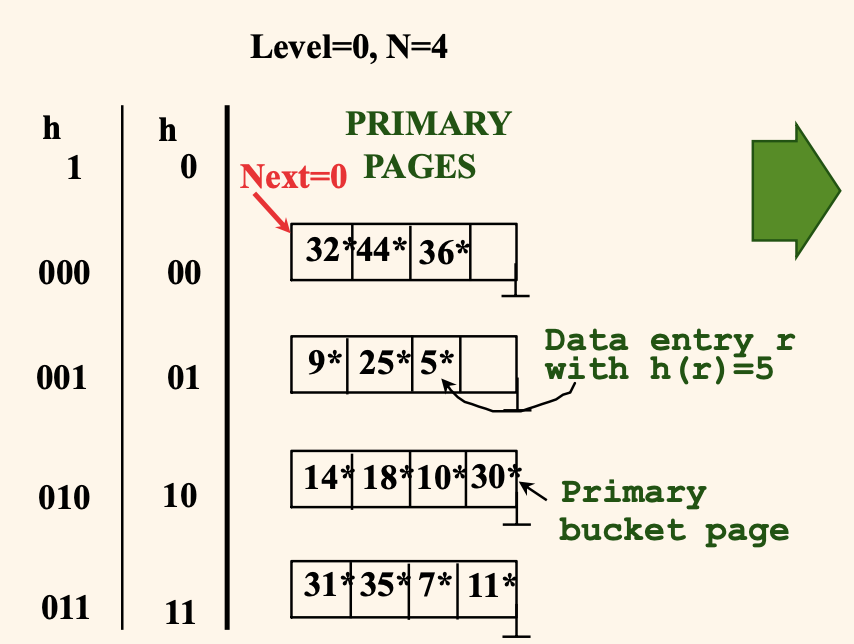
이때 현재 4개의 버켓에 위와 같이 데이터가 들어있는 상황을 생각해보자.
각각의 버켓은 4개의 데이터 엔트리를 가지며, h₀ 해시 함수는 h(key) % 4*2^0 의 결과에 맞춰 0 ~ 3 의 나머지 값을 기준으로 데이터를 분류해서 저장한다.
선형 해싱은 (다양한 알고리즘이 존재할 수 있으나 이번 예시에서는) 새로운 데이터 엔트리를 추가할 때 오버플로우 페이지가 생기는 경우, 버켓을 분할한다.
예를 들어 위 그림과 같은 상황에서 43 이라는 데이터 엔트리를 추가하려고 한다고 해보자.
그러면 43을 4로 나눈 나머지는 3 이므로 h₀ 에서 '11' 위치에 데이터 엔트리를 추가하려고 할 것이다.
그런데 이 버켓이 현재 모두 다 차있기 때문에 오버플로우 페이지를 만들어 43을 저장한다.
그러면 <31, 35, 7, 11> - <43, , , > 과 같이 저장될 것이다.
이때 새로운 오버플로우 페이지가 생겼으므로, Next 변수가 가리키고 있는 버켓을 분할한다.
(오버플로우가 발생하는 버켓이 아니라, Next 변수가 가리키는 버켓이다. 이 둘은 서로 다를 수 있다!)
분할한 뒤에는 h₁ 함수를 사용하여 기존의 32, 44, 36 을 8로 나눈 나머지가 0인 것과 4인 것으로 분할하여 저장한다.
분할이 완료되면 Next 변수가 1 증가하며, 최종 결과는 아래와 같다.

현재 라운드가 Level 인 상태에서는 0부터 Next - 1 까지는 분할된 버켓이고, Next ~ N_Level 까지는 분할되지 않은 버켓이다.
(N_Level 은 현재 레벨이 갖는 전체 버켓의 수 = N * 2^Level 이다.)
위 그림을 예시로부면, 현재 Level = 0 인 상태에서 0부터 Next - 1 = 0 까지는 분할된 버켓이고 (0번 버켓은 분할되어 있다.)
Next ~ N_Level → 1 ~ 4 까지는 아직 분할되지 않은 버켓이다.
어떤 key 값을 h₀ 해시 함수에 적용했을 때 그 값이 0 이라면, 0은 분할된 버켓이므로 h₀ 만으로는 초기 버켓과 새로 분할되어 떨어져나간 버켓 중 어떤 버켓에 들어가야 할 지 알 수 없으므로 h₁ 을 적용하여 8로 나눈 나머지를 계산함으로써 데이터 엔트리를 추가할 버켓을 결정한다.
반면 어떤 key 값을 h₀ 해시 함수에 적용했을 때 그 값이 1~3 사이라면, 분할디지 않은 버켓이므로 그 버켓에 그대로 추가하거나, 오버플로우 페이지를 만들어서 데이터를 추가하고 Next 버켓을 분할하는 과정을 거친다.
예를 들어 37 이라는 데이터를 신규로 추가하는 경우, h₀(37) = 01 이므로 <9, 25, 5, 37> 로 데이터가 추가되며, 이때는 오버플로우 페이지가 생기지 않아서 버켓 분할이 발생하지 않는다. (따라서 Next 변수의 변화도 없다.)
그런데 어떤 경우에는 Next 가 가리키는 버켓이 가득 차 있고, 새로 추가하려는 데이터가 Next 가 가리키는 버켓에 추가되어야 하는 상황이 있을 수도 있다.
29 라는 신규 데이터를 추가하려는 상황을 생각해보자.
h₀(29) = 01 로 계산한 버켓에 데이터를 넣으려는데, Next = 1 이 가리키는 버켓에 29를 추가로 저장하려는 상황이다.
이때는 오버플로우 페이지를 만들 필요 없이, Next 가 가리키는 버켓을 분할하고, 29를 기존 버켓과 분할된 버켓 중 h₁(29) 가 가리키는 버켓에 담으면 된다.
최종 결과는 001 이 <9, 25, , > 를 가리키고, 101 이 <5, 37, 29, > 를 가리키는 방향으로 버켓이 분할된다.
다음으로 Level 이 증가하는 상황을 살펴보자.
마지막 상태에서 22, 66, 34 를 추가적으로 삽입했다고 해보자.
셋 모두 h₀ 해시 함수의 적용 결과가 2 이므로 이진수로 10 이 가리키는 버켓에 데이터가 추가되려고 하며,
오버플로우 페이지가 생기기 때문에 버켓이 분할되고 Next = 3 으로 증가하게 된다.
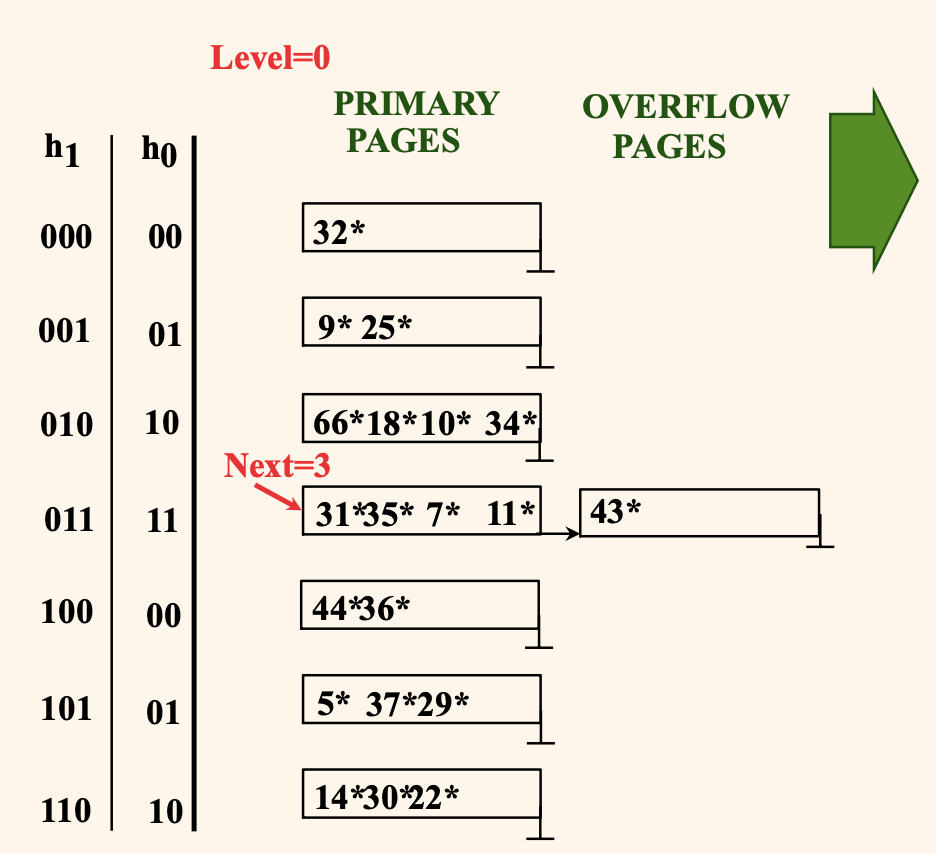
그 상황을 그림으로 나타내면 위와 같다.
이제 Next = 3 이 N_Level - 1 과 같은 상황에서 추가적으로 분할이 발생하는 상황을 생각해보자.
위 그림과 같은 상황에서 50이라는 신규 데이터가 들어오면, 이 데이터의 h₁ 적용 결과는 010 이므로 데이터 분할이 발생하게 된다.
(h₀ 적용 결과인 2는 0 ~ (3-1) 사이 이므로 분할된 버켓의 범위에 속한다. 따라서 버켓 위치를 알아내려면 h₁ 을 사용해야 한다.)
이때 50은 오버플로우 페이지에 저장되고, Next = 3 이 가리키는 버켓이 분할되어 기존의 오버플로우 페이지가 사라진다.

이렇게 현재 레벨에 대해 N_Level 에 Next가 도달하게 되면, 이때 Level 이 1 증가하고, Next = 0 으로 초기화되어 새로운 라운드를 시작한다.
Level 이 증가하면 결론적으로 키가 해시되는 실질 유효범위가 2배로 늘어난 것과 같다.
선형 해싱의 연산 비용
선형 해싱은 위와 같은 방법으로 데이터 엔트리를 관리하기 때문에, 동등 조건 탐색 시 오버플로우 페이지가 없다면 1번의 디스크 입출력으로 원하는 데이터 엔트리를 찾을 수 있다.
(실제로 데이터 분포가 균등하다면 평균적으로 1.2번의 디스크 입출력이 발생한다.)
하지만 데이터가 편중되어있다면 한쪽 버켓에 계속 데이터가 몰리면서 공간 활용도가 낮아지고 비용 또한 편중된 데이터 엔트리 수에 비례하여 증가한다.
데이터 삽입의 경우, 오버플로우가 발생하지 않으면 각각 1번의 읽고, 쓰기를 통해 데이터 엔트리를 추가할 수 있다.
데이터 삭제의 경우, 삽입과 반대로 이루어지며, 삭제를 통해 오버플로우 버켓이 비게되면, 해당 버켓을 제거함과 동시에 Next 변수를 1 감소시킨다. (만약 Next = 0 이었다면 Level 이 감소하고 N_Level - 1 위치를 Next가 가리킬 것이다.)
그리고 적절한 기준을 적용하여 분할된 버켓을 하나로 합병하는 과정이 일어난다. (책에서 자세히 다루지는 않았다.)
확장성 해싱 vs 선형 해싱
선행 해싱을 일종의 변형된 확장성 해싱처럼 생각해보자.
그러면 선형 해싱은 첫번째 분할을 반드시 0번 버켓에서 발생시키고, N번 버켓이 생성된다.
기존 확장성 해싱의 관점에서보면 이 시점에서 디렉토리가 2배가 되어야 하지만, 선형해싱에서는 실제로 2배가 되지 않는다.
두 번째 분할은 반드시 1번 버켓에서 발생하고, 이로 인해 N+1번 버켓이 생성되는 과정을 거치면서 처음 N개의 버킷이 모두 분할되어야 실제로 2배가 된다.
해시 함수의 선택 과점에서도 확장성 해싱에서는 디렉토리를 한번에 2배로 만들었지만, 선형 해싱에서는 h₀ h₁ 을 모두 사용하면서 점진적으로 2배로 늘리는 과정을 거친다.
선형 해싱은 라운드 로빈을 통해 공평하게 하나씩 모두 분할하다보면 디렉토리 없이도 오버플로우 체인을 적절한 선에서 관리할 수 있다는 아이디어를 사용한다.
반면 확장성 해싱은 항상 그 순간에 오버플로우가 발생하는 버켓을 분할하므로 분할 횟수가 상대적으로 적어 버켓 적재율을 높일 수 있다.
(즉, 쓸모없는 분할된 버켓이 없다.)
따라서 데이터가 균등하게 분포되어 있을 대는 선형 해싱으로 구현되어 있을 경우 등호 조건 조회에 대한 비용이 낮아진다.
(디렉토리 계층이 존재하지 않기 때문)
하지만 데이터가 편중된 경우에는 빈 버켓을 계속 만들어내므로 적재율이 낮아지고, 높은 적재율을 갖는 확장성 해싱에 비해 성능이 낮아지게 된다.
'CS > 기초데이터베이스' 카테고리의 다른 글
| [데이터베이스] 22. 외부 정렬 (0) | 2024.11.29 |
|---|---|
| [데이터베이스] 21. 질의 수행 (Query Plan) (2) | 2024.11.29 |
| [데이터베이스] 19. 트리 기반 인덱스 (B+트리) (1) | 2024.10.22 |
| [데이터베이스] 18. 파일과 인덱스 (레코드 저장 방법) (0) | 2024.10.22 |
| [데이터베이스] 17. 하드 디스크와 SSD의 구조 (0) | 2024.10.22 |
