데이터베이스에서는 다양한 이유로 레코드를 정렬해야 할 때가 있다.
- order by 와 같은 SQL을 처리해야 할 수도 있고
- 트리 인덱스에 데이터를 많이 넣고자 할 때도 정렬이 필요하고
- projection 연산 결과로 중복을 제거할 때도 정렬이 유용하며
- 조인을 구현할 때 정렬을 사용하여 조인할 수도 있다.
우리가 흔히 쓰는 정렬 알고리즘은 in place 방식이라고 하더라도 O(N)의 공간복잡도가 필요하다.
하지만 요즘 메인 메모리의 크기가 점점 늘어나고는 있음에도 처리해야 할 데이터는 너무 많아서 메인 메모리만으로는 모든 데이터를 한번에 정렬할 수 없다.
그렇다고 디스크를 메모리처럼 보고 정렬하기에는 너무 많은 입출력 비용이 발생하기 때문에 디스크 접근 비용을 최소화하면서 적은 메모리로 데이터를 정렬하는 '외부 정렬' 알고리즘이 필요하다.
단순 이원 합병 정렬

먼저 단순하게 위 그림과 같이 메인 메모리에 3개의 버퍼 페이지가 있다고 해보자. (실제로는 더 많은 버퍼 페이지를 쓸 수 있다.)
하나의 파일을 정렬하는 과정에서 중간 과정에 여러개의 정렬된 서브 파일들이 생성되는데, 이 서브 파일들을 '런(run)' 이라고 부른다.
3개의 버퍼 페이지 중 2개는 정렬할 페이지를 받는 버퍼 페이지 이고, 하나는 정렬 결과를 내보내는 페이지이다.
하나의 파일을 정렬할 때, 그 파일이 메모리에 다 들어가지 않더라도, 그 파일을 더 작은 여러 개의 서브파일로 쪼개고, 각각의 서브파일을 정렬한 결과를 합병하면 결국 전체 파일을 정렬할 수 있다. 이때 각각의 정렬 단계를 '패스(pass)' 라고 부른다.
단순 이원 합병 정렬의 알고리즘은 다음과 같다.
1. 첫 번째 패스
파일에 있는 페이지들을 한번에 하나씩 읽어들이고, 그 내부의 레코드를 정렬한 뒤, 정렬된 페이지 (1페이지 크기의 정렬된 런)를 디스크에 쓴다.
한 페이지 내부의 레코드를 정렬할 때는 메인 메모리에 페이지 데이터가 모두 올라와있는 상태니 기존에 사용하는 내부 정렬 알고리즘을 활용하여 정렬할 수 있다. (퀵소트, 머지소트, ..)
2. 두 번째 패스 이후
앞 패스에서 생긴 런을 2개씩 읽어들인 뒤, 2배 크기의 정렬된 런을 만들도록 합병한다.
이를 일반화하면 2ᵏ 개의 페이지로 구성된 하나의 파일을 정렬하는 과정은 다음과 같다.
패스 0 : 1페이지 크기의 정렬된 런을 2ᵏ개 생성
패스 1 : 2페이지 크기의 정렬된 런을 2ᵏ⁻¹ 개 생성
패스 2 : 2² 페이지 크기의 정렬된 런을 2ᵏ⁻² 개 생성
...
패스 k : 2ᵏ 페이지 크기의 정렬된 런을 1개 생성
각 패스에서는 결과적으로 하나의 파일을 구성하는 모든 페이지를 읽고 쓰는 과정을 1번씩 수행하므로 2번의 디스크 입출력이 발생한다.
따라서 파일을 구성하는 페이지의 수가 N 이라면 디스크 입출력 횟수는 2N (log₂ N + 1) 이다.
구체적인 예시를 따라가보자.

먼저 그림에서 하나의 사각형은 하나의 페이지를 나타낸다.
위 그림은 하나의 페이지에 2개의 레코드가 들어있고, 7개 페이지로 구성된 하나의 파일을 나타낸다.
(색칠한 사각형은 없는 페이지라고 생각하자)
- 패스 0
패스 0 에서는 한번에 하나의 파일을 읽어들이고 CPU를 사용해 내부 정렬을 수행하여 페이지 내 레코드를 정렬한 뒤 그 결과를 run 으로 내보낸다. 이 결과 위에서 정리한대로, 1페이지 크기의 정렬된 런이 7개 생성된다.
이때 페이지는 버퍼 페이지의 input, output 버퍼 페이지를 통해 들어오고 나간다.

- 패스 1
이제 이전 패스의 결과로 생성된 런 2개를 input page 로 받아들인다.
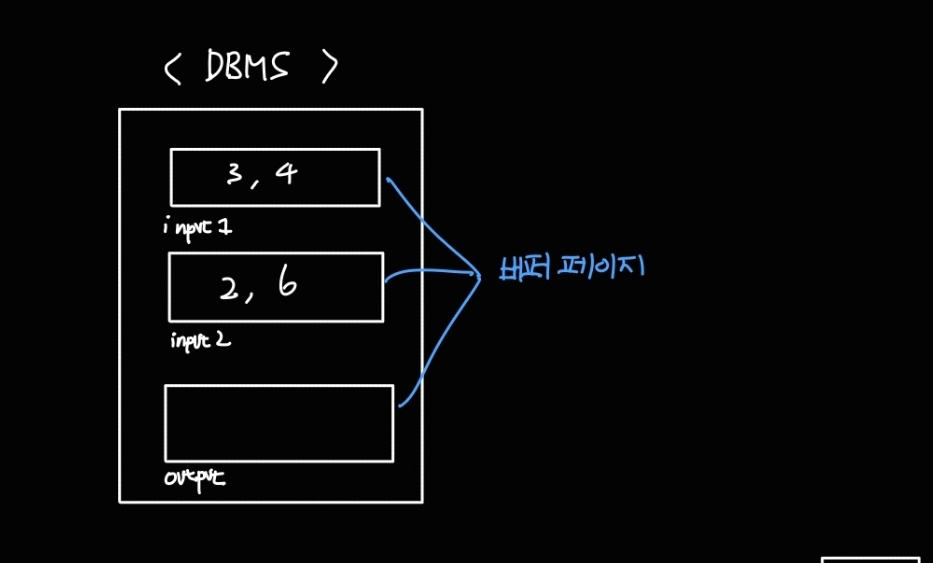
처음에는 <3, 4> 페이지와 <2, 6> 페이지가 들어올 것이다.
각 페이지 내 레코드는 모두 정렬되어 있으므로 머지 소트에서 병합하듯, 각 페이지의 앞에 있는 레코드를 비교하여 크기 순으로 output page에 쓰고 디스크로 내보낸다.

첫 정렬 결과로 <2, 3> 레코드로 구성된 하나의 페이지가 만들어지고 디스크에 쓰인다.
패스 1에서는 1페이지 크기의 런 2개를 읽어들여 2페이지 크기의 런 하나를 만드므로, 나머지 4, 6을 모아 <4, 6> 페이지로 만들 것이다.

정렬 결과는 위와 같다.
이 과정을 나머지 pass 0 결과에 대해 반복하면 아래와 같은 pass 1 결과가 나온다.

- 패스 2
패스 2에서는 이전 정렬의 결과로 생성된 2페이지 크기의 런 2개를 병합하여 4페이지 크기의 런 1개를 만든다.
위 예시에서는 <2, 3> <4, 6> 과 <4, 7> <8, 9> 를 병합할 것이다.
구체적인 과정은 아래와 같다.
1. 각 런에서 제일 앞에 있는 페이지를 가져와 정렬한다.

처음엔 <2, 3> 과 <4, 7> 을 가져올 것이다.
그 결과는 <2, 3> 이 되며 <2, 3> 페이지가 output으로 빠져나간다.
첫번째 런의 첫번째 페이지를 모두 처리했으니, 그 다음 페이지를 input 으로 불러온다.

그 다음에는 <4, 6> 과 <4, 7> 을 병합한다.
각 페이지에서 앞에 있는 레코드를 비교하여 <4, 4> 를 output 페이지로 만들어 내보낸다.

그 결과로 이렇게 하나의 레코드씩 남은 페이지가 2개 남는다.
이때는 두 레코드롤 병합해서 하나의 페이지로 옮기고 다시 아직 읽지 않은 페이지를 불러와서 병합한다.
(<6, 7> 을 바로 내보낼 수는 없다. 아직 읽지 않은 페이지에서 더 작은 데이터가 들어있을 수도 있기 때문이다.
위 상황에서 6대신 9가 들어있었다고 생각해보면 이해가 된다.)

그래서 이렇게 6을 하나의 페이지로 몰아주고, (메모리 내부에서는 충분히 이렇게 정렬할 수 있다.)
<8, 9> 페이지를 읽어와서 같은 과정으로 병합한다.
최종적으로 pass 1 을 거친 결과는 아래와 같다.
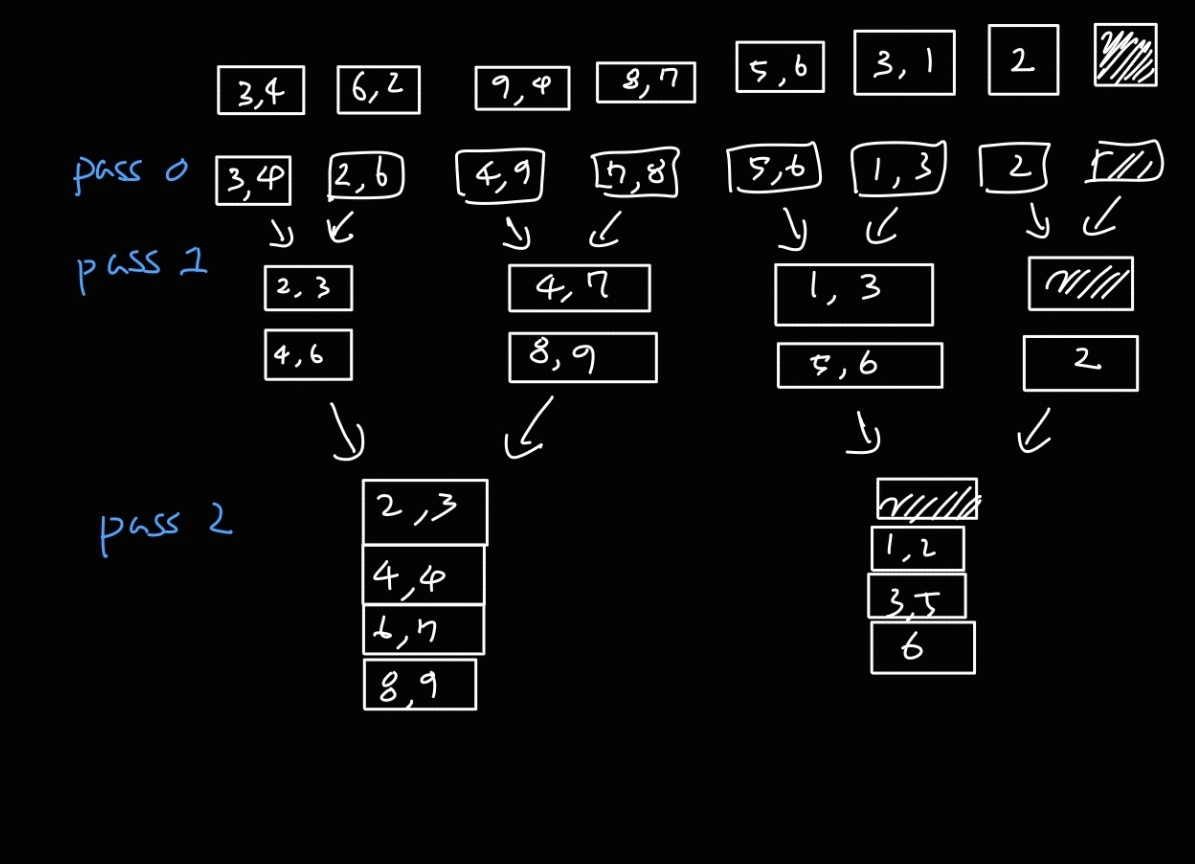
- 패스 3
패스 3은 이제 같은 방법으로 병합할 수 있음을 쉽게 이해할 수 있을 것이다.
결과는 아래와 같으며, 7개 페이지로 구성된 1개의 런이 나왔으므로 최종 정렬 결과가 된다.

외부 정렬
지금은 단순하개 3개의 버퍼 페이지로 구성된 메모리로 2개의 input 씩 받아들여 처리했지만, 이를 일반화할 수 있다.
만약 메모리에 B개의 버퍼 페이지를 쓸 수 있고, N개의 페이지로 구성된 파일 하나를 정렬하는 경우, 패스 0에서 한번에 B개씩 페이지를 읽고 내부 정렬하여 B개씩의 페이지로 구성된 ceil(N/B) 개의 런을 만들어 낼 수 있다. (기존의 패스0과 패스 1을 한번에 수행한 것이다.)
이후 패스에서는 입력으로 B-1개의 버퍼 페이지를 사용하고, 1개의 출력 버퍼 페이지를 사용하여 각 패스마다 (B-1)원 합병을 수행한다.
이 경우 정렬에 필요한 총 패수의 수는 ceil(Log_(B-1) N) + 1 이 될 것이다.
만약 정렬이 자주 필요하다면 애초에 인덱스를 만들 때 B+ 트리로 만들어서 정렬된 상태를 유지하도록 만들 수 있다.
이렇게 하면 초기에 트리를 구성하고 유지하는 비용이 존재하겠지만, 매 순간 정렬된 결과에 대해 연산이 필요한 경우 정렬 비용을 절약할 수 있다.
예를 들면
10 페이지를 5개 버퍼로 정렬하는 경우,
ceil(log_4(ceil(10/5))) + 1 = ceil(log_4(2)) + 1 = ceil(0.5) + 1 = 1 + 1 = 2 로 2개의 패스가 필요하다.
250 페이지를 5개 버퍼로 정렬하는 경우,
ceil(log_4(ceil(250/5))) + 1 = ceil(log_4(50)) + 1 = ceil(2.xxx) + 1 = 3 + 1 = 4 로, 4개의 패스가 필요하다.
'CS > 기초데이터베이스' 카테고리의 다른 글
| [데이터베이스] 24. 트랜잭션 & 직렬 가능성 (0) | 2024.12.07 |
|---|---|
| [데이터베이스] 23. Postgresql Explain (0) | 2024.12.05 |
| [데이터베이스] 21. 질의 수행 (Query Plan) (2) | 2024.11.29 |
| [데이터베이스] 20. 해시 기반 인덱스 (0) | 2024.11.22 |
| [데이터베이스] 19. 트리 기반 인덱스 (B+트리) (1) | 2024.10.22 |
