SQL 문장을 실제로 컴퓨터가 실행할 때는 어떤 과정으로 실행될까?
먼저 SQL은 확장된 형태의 관계 대수로 변환된다.
그리고 이 관계 대수식을 기반으로 '질의 처리 계획'을 만드는데, 이는 관계 대수 연산자를 노드로 하는 트리로 표현된다.
트리의 각 노드에는 해당 연산자가 어떤 알고리즘을 사용할 것인지 표시하는 라벨이 있다.
이렇게 관계 대수 연산자는 질의 수행의 기본 단위가 되며, 이 연산자들의 동작을 구현하는 것은 최대 성능을 위해 최적화 되어 있다.
시스템 카탈로그
DBMS가 쿼리를 처리할 때, 어떻게 처리할 지 결정하는 과정에서 테이블의 구조와 인덱스 등의 데이터를 참고한다.
이 정보는 '시스템 카탈로그'라는 특별한 '테이블' 에 저장된다. (데이터 딕셔너리, 카탈로그라고 부르기도 한다.)
실제 테이블 데이터와 인덱스의 데이터 엔트리는 앞에서 정리했던 '파일'에 저장되지만,
DBMS가 관리하고 있는 모든 테이블과 그 인덱스들의 메타 데이터에 대한 테이블이 카탈로그라고 보면 된다.
카탈로그에는 대략적으로 다음과 같은 정보가 들어간다.
- 테이블 관련 정보 : 테이블명, 파일 이름, 파일 구조 (힙, 정렬힙, 인덱스 ..), 속성 명, 속성 타입, 인덱스, 무결성 제약조건, ..
- 인덱스 관련 정보 : 인덱스 이름, 인덱스 구조 (해시, 트리, ..), 탐색키
- 뷰 관련 정보 : 뷰 이름, 뷰 정의
또한 이런 메타데이터 외에도 테이블과 인덱스에 대한 '통계' 정보도 들어간다.
이 정보는 테이블 내용이 바뀔 때마다 바꾸기엔 비용이 비싸서, 일정 주기마다 갱신한다.
여기에는 cardinality, 테이블의 페이지 수, 인덱스 카디널리티, 인덱스 페이지 수, 인덱스 높이, 인덱스 범위 등이 저장된다.
참고로 시스템 카탈로그 역시 '테이블' 이라서, 카탈로그 자신에 대한 메타데이터 역시 카탈로그 테이블 안에 들어있다.
관계대수 연산자 수행
관계 대수 연산자의 동작을 실제로 구현할 때는 여러 알고리즘이 존재한다.
이때 하나의 알고리즘을 고정적으로 사용하기 보다, 각각의 상황에 맞게 최적의 알고리즘을 선택하여 동작을 구현하는데, 테이블의 크기, 인덱스 유무, 정렬 순서, 버퍼 풀의 크기 등을 고려하여 알고리즘이 선택된다.
먼저 관계 대수 연산자의 동작을 실제로 구현하는 알고리즘은 대표적으로 다음 3가지가 있다.
1. 인덱싱 (Indexing) : 관계 대수에서 selection, join 이 명시되면, 그 조건에 맞는 튜플을 선별하기 위해 인덱스를 사용할 수 있다.
2. 반복 (Iteration) : 테이블의 모든 레코드를 하나씩 검사하는 연산. 만약 레코드의 일부 필드가 필요한데, 그 필드들이 모두 인덱스의 탐색키에 존재하면, 인덱스 파일 내의 데이터 엔트리를 탐색하는 것으로 대신할 수 있다.
3. 분할 (Partitioning) : 특정한 정렬 키 기준으로 튜플을 정렬한 뒤 정렬 키를 기준으로 튜플을 분할하거나, 해싱을 사용해서 같은 해시값을 갖는 튜플끼리 모아서 분할할 수 있다. 이렇게 튜플을 분할하면 하나의 시간이 오래걸리는 연산을, 작은 크기의 튜플들에 대한 연산 여러개로 나눌 수 있다.
접근 경로 (Access Path)
접근 경로는 테이블로부터 튜플을 검색하는 구체적인 방법을 말한다.
내가 원하는 튜플을 검색하기 위해서는 특정 조건에 맞는 튜플들을 선택해야 하는데, 이때 파일을 스캔하거나, index와 조건이 맞는 튜플을 찾을 수 있다.
<테이블 속성> op <값> 형태로 하나의 <조건>을 나타낼 때, (op 는 비교연산자)
각각의 <조건> 을 and 연산자(논리곱)로 묶은 단순한 형태의 selection 을 논리곱 정규형 (CNF, conjunctive normal form) 이라고 한다. 예를 들어 (age > 10) and (sal >= 1000) 과 같은 조건을 갖는 selection 연산은 CNF 이다.
이때 인덱스를 사용하여 특정 튜플의 조건이 맞는지 확인하려면
- 해시 인덱스
<테이블 속성> = <값> 형태의 <조건> 만 확인할 수 있으며, 이때 해시 인덱스의 탐색키가 여러 속성의 조합으로 되어있다면 모든 속성이 <조건>에 들어있어야 한다.
예를 들어 <a, b, c> 라는 탐색키로 이루어진 해시 인덱스가 있다면, 반드시 a = 10 and b = 20 and c = 30 과 같은 형태의 조건이어야 CNF에 맞는지 확인할 수 있다.
a = 10 만 있다거나, a > 10 and b = 10 과 같이 = 연산자 이외의 연산자가 존재하면 확인할 수 없다.
- 트리 인덱스
<a, b, c> 라는 탐색키로 이루어진 트리 인덱스가 있다면, 이 조합의 prefix 에 대해서 조건을 체크할 수 있다.
<a, b, c> 의 prefix 는 <a>, <a, b>, <a, b, c> 이다.
<a, c>, <b, c>, <c> 와 같은 조합의 CNF는 확인할 수 없다.
하지만 트리 인덱스는 연산자의 제약이 없다.
우리가 원하는 튜플 조합을 가져올 때, 그 구체적인 방법(접근 경로)은 여러 가지가 있을 수 있다.
예를 들면 어떤 테이블에 주어진 셀렉션 조건에 맞는 튜플을 가져온다고 할 때, 우리는 최소 2개의 접근 경로를 알고 있다.
(file 에 직접 접근하여 레코드 스캔, index 사용하여 레코드 스캔) 경우에 따라서는 인덱스만을 스캔하여 데이터를 얻어올 수도 있다.
이때 여러 접근 경로 중에서 page I/O 가 제일 적은 접근 경로를 가리켜 Most Selective Access Path 라고 부른다.
관계 대수의 selection 연산을 실제로 구현할 때는 most selective access path 를 찾고, 이 접근 경로를 따라 튜플을 가져온 뒤, index를 적용할 수 없는 항에 적용한다.
인덱스를 사용하여 CNF의 일부 항을 결정하면 테이블로부터 가져올 튜플의 개수를 줄일 수 있다.
예를 들어 day < 8/9/94 and bid = 5 and sid = 3 과 같은 셀렉션 조건이 있다고 해보자.
만약 B+ 트리 기반의 인덱스를 적용하는 경우, day 항에 대해 B+ 트리 기반 인덱스를 적용한 뒤, 이 인덱스로 얻어온 모든 튜플에 대해서 bid = 5, sid = 3 을 체크하면 된다.
만약 <bid, sid> 에 대해 해시 인덱스를 적용한다면, 이렇게 해서 가져온 모든 튜플에 대해 day < 8/9/94 인 항을 추가적으로 선별하는 과정을 통해 원하는 데이터를 얻어올 수 있다.
관계 대수 연산 비용 계산
이제부터 예시 테이블을 하나 보면서 질의 수행 과정과 비용에 대해 정리한다.
예시 테이블은 Sailors, Reservers 2개 테이블이며, 그 스키마는 앞서 정리한 것과 같다.
Reserves 테이블의 하나의 튜플은 40 바이트의 크기를 갖고, 한 페이지에는 100개의 Reserves 테이블 튜플이 들어갈 수 있다.
Reserves 테이블의 데이터는 1000개 페이지에 걸쳐 존재한다.
Sailors 테이블의 하나의 튜플은 50 바이트의 크기를 갖고, 한 페이지에는 80개의 Sailors 테이블 튜플이 들어갈 수 있다.
Sailors 테이블의 데이터는 500개 페이지에 걸쳐 존재한다.
셀렉션
셀렉션 연산의 비용은 조건에 맞는 튜플의 개수와 인덱스의 클러스터링(군집) 여부에 따라 달라진다.
그 비용은 일치하는 튜플을 찾는 비용 + 튜플을 가져오는 비용으로 계산한다.
튜플을 찾는 비용은 상대적으로 작으며, 튜플을 가져오는 비용은 군집 인덱스가 아닌 경우 클 수 있다.

예를 들어 다음과 같은 SQL을 실행한다고 해보자.
관계 대수로는 R.rname < 'C%' 조건에 맞는 셀렉션 연산으로 표현할 수 있다.
만약 모든 이름들의 분포가 균등하다고 가정하면 첫 글자가 C일 확률은 대략 10% 정도로 잡을 수 있다.
( 1 / 26 이면 대략 5% 정도로 잡는게 낫지 않을까..? 일단 책에서는 10%로 잡았다. )
따라서 조건에 맞는 Reserves 테이블의 레코드는 1000페이지 * (100 레코드 / 페이지) = 10만 레코드가 존재하므로 대략 1만개의 레코드를 가져와야 하며, 페이지로는 100 페이지를 가져와야 한다.
만약 트리 기반 인덱스 사용한다면, 군집 인덱스일 경우 대략 100번이 입출력을, 비군집 인덱스인 경우 최악의 경우 1만번의 입출력을 수행할 수 있다.
(보통 전체의 5% 이상의 튜플을 찾는 경우, 비군집 인덱스라면 전체 스캔이 더 효율적일 수도 있다.)
프로젝션
입력 테이블의 특정 필드를 삭제하는 연산.
관계 대수 정리할 때 언급했듯, 기본적으로 프로젝션은 중복 데이터를 제거하는 연산이므로, 비용이 많이 든다.
중복을 제거하는 방법을 구현할 때, 일반적으로는 위에서 정리한 partition 을 활용하여 중복을 제거한다.
만약 Reserves 테이블에서 <sid, bid> 쌍 데이터를 조회하는 경우, 먼저 Reserves 테이블을 스캔하고, <sid, bid> 를 정렬키로 하여 정렬하여 Reserves 테이블을 분할한다.
이제 정렬된 <sid, bid> 쌍을 스캔하면서 인접한 중복 값을 제거하면 중복을 간단하게 제거할 수 있다.
(테이블의 모든 튜플 데이터를 정렬하는 구체적인 방법은 다음 글에서 정리한다.)
만약 <sid, bid> 가 인덱스의 탐색키로 존재한다면, 테이블을 스캔하는 대신, 인덱스 데이터 엔트리를 스캔하여 정렬하면 더 적은 비용으로 정렬할 수 있다.
partition 연산은 해싱을 통해서도 구현할 수 있었다.
<sid, bid> 쌍을 해싱하고, 해시값을 기반으로 파티션을 생성한다.
메모리에는 한번에 하나의 파티션을 불러와 그 파티션 내 데이터에 대해 중복을 제거한다.
조인
Reserves.sid = Sailors.sid 인 Reserves 테이블과 Sailors 테이블 조인 연산을 생각해보자.
기본적으로 조인은 두 테이블에 대한 cross product 로 이루어지므로, 이중 반복문을 돌아야 한다.
만약 Sailors 테이블의 sid 에 인덱스가 존재한다면, 이 조인 연산을 수행할 때는 인덱스가 존재하는 Sailors 테이블에 대한 스캔을 안쪽 루프에 넣어서 돌리면 더 효율적이다.
즉 아래 그림과 같이 실제 조인 연산을 수행하는 것이 좋다.
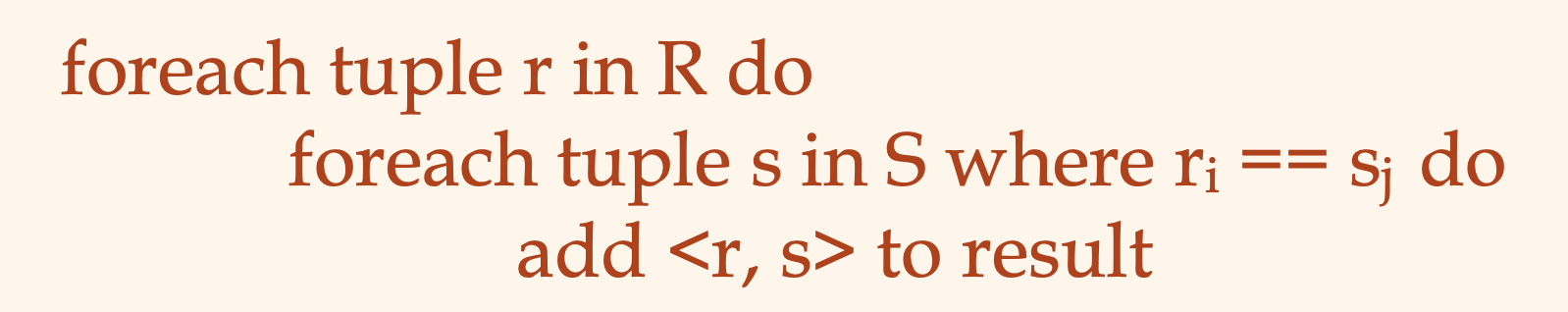
이렇게 인덱스가 걸려있는 테이블을 안쪽에 넣는 것을 '인덱스 중첩루프 조인' 이라고 한다.
인덱스 중첩루프 조인 방법의 조인 비용은 아래와 같이 계산할 수 있다.
먼저 밖에서 루프를 도는 Reserves 테이블의 페이지 로딩 비용은 1000 이다. (1000 페이지를 읽어들이므로)
Reserves 테이블에는 페이지당 100개의 레코드가 있으므로 10만개 레코드 각각에 대해 그 레코드에 일치하는 sid 를 Sailors 테이블에서 찾는다.
해시 기반인덱스에서는 sid 로부터 레코드가 존재하는 인덱스 페이지를 얻어오는데 평균적으로 1.2 번의 입출력이 필요하고,
인덱스의 데이터 엔트리로부터 실제 데이터 레코드가 존재하는 페이지를 가져오는 1번의 입출력 비용이 든다.
따라서 1000 개 페이지의 Reserves 테이블 페이지를 읽어들인 뒤, 그 안에 있는 10만 개의 Reserves 테이블 레코드 각각에 대해, 매번 해시 연산으로 평균 1.2번의 페이지 입출력으로 데이터 엔트리가 들어있는 인덱스 페이지를 찾고, 실제 데이터 레코드를 가져오기 위해 페이지를 1번 가져와서 총 (1.2 + 1) 번의 페이지 연산을 해야 하므로, 1000 + 2.2 * 10만 = 22만 1000번의 페이지 입출력 비용이 든다.
(sname 필드를 골라오려면 데이터 엔트리를 가져온 뒤, 데이터 엔트리에 들어있는 rid 를 기반으로 실제 페이지를 불러와서 sname을 포함한 모든 속성을 가져와야 한다.)
만약 인덱스를 쓰지 않고 그냥 풀스캔하면, 1000페이지를 로딩하고, 10만개 레코드 각각에 대해 500 페이지를 읽어들여서 일치하는 레코드를 찾아내므로 1000 + 10만 x 500 = 5000만 1000번의 페이지 입출력 비용이 필요했다.
이에 비하면 비용이 매우 많이 줄어든 것을 알 수 있다.
이 비용은 인덱스가 군집인지, 비군집인지에 따라 달라질 수 있다.
만약 인덱스가 트리 기반이라면 평균 인덱스 페이지 로딩 비용은 2~4로 증가한다.
만약 Reserves 테이블에 인덱스가 걸려있어 루프의 안쪽에 넣으면 어떻게 될까?
먼저 모든 Sailors 데이터를 가져와야 하므로 500개 페이지를 불러온다.
그리고 그 안에 있는 500 * 80 = 4000 개 튜플에 대해 반복하면서 Sailors.sid 와 일치하는 Reserves.sid 를 갖는 튜플을 찾는다.
Reserves 테이블에도 sid 에 인덱스가 걸려있고, 데이터가 균등하게 분포되어 있어 한 명의 선원이 평균적으로 2.5번의 예약을 했다면 군집인덱스의 경우 1번의 페이지 입출력이 (sid 가 모여있으므로), 비군집 인덱스라면 평균 2.5번의 페이지 입출력이 발생한다.
비군집 기준이라면 500 + 4000 * (1.2 + 2.5) → 500 + 4000 * 4 = 대략 16500 번의 페이지 입출력 비용이 발생한다.
인덱스 중첩루프 조인은 두 테이블 중 적어도 하나의 조인 조건에 인덱스가 걸려있어야 한다.
만약 조인 조건 필드에 대한 인덱스가 두 테이블 모두 걸려있지 않다면 인덱스 중첩루프 조인을 쓸 수 없다.
이럴 때는 두 테이블 데이터를 모두 정렬하고, 정렬된 레코드를 동시에 스캔하면서 조인 결과를 얻어낼 수 있다.
이 방법을 가리켜 '정렬합병 조인 (sort-merge join)' 이라고 한다.
정렬에 대한 구체적인 내용은 다음 글에서 정리하겠지만, 만약 정렬하는데 2번의 패스가 필요하다면,
Reserves 테이블의 레코드를 정렬하는 데 드는 입출력 비용은 2 * 2 * 1000 = 4000
Sailors 테이블의 레코드를 정렬하는데 드는 입출력 비용은 2 * 2 * 500 = 2000 이다.
(1개 페이지 내 데이터를 정렬할 때 2번의 패스가 필요한데, 각 패스에서 1번의 입력, 1번의 출력이 발생하므로 입출력이 2번 발생한다.)
정렬을 마친 후에는 두 테이블의 정렬된 데이터를 모두 1번씩 순회하면 되므로 총 조인 비용은
정렬 비용 (4000 + 2000) + 순회 비용 (1000 + 500) = 7500 이다.
정렬 합병 조인은 인덱스 중첩루프 조인보다 비용이 낮지만, 인덱스 중첩루프 정렬은 데이터의 크기에 따라 점진적으로 비용이 증가하므로, 바깥 루프를 순회하는 레코드의 수가 적다면 더 낮은 비용을 가질 수 있다.
정렬 합병 조인은 두 테이블을 적어도 한번씩 모두 순회해야 하지만, 인덱스 중첩 루프 조인은 특정 조건에 해당하는 데이터에 대해 조인하는 경우, 그 데이터에 대해서만 바깥 루프를 순회하며 조인하면 되므로 조인 비용이 더 낮아질 수 있다.
질의 최적화기 (Query Optimizer)
지금까지는 하나의 관계 대수 연산을 수행하는 방법과 그 비용을 살펴보았다.
하지만 실제로 하나의 질의를 수행할 때는 여러 관계 대수 연산이 복합적으로 섞여있다.
관계대수 질의 최적화기는 하나의 질의가 주어질 때 이 질의를 수행하는 여러 개의 질의 계획 (query plan)을 만들고, 이 계획들 중 추정 비용이 제일 작은 계획을 선택하여 수행한다.
질의 비용을 추정할 때는 시스템 카탈로그에 저장된 통계 내용을 활용하여 각각의 관계 대수 연산 수행 비용과 각 연산의 결과 크기를 추정한다. (위에서 정리한 것처럼 프로젝션, 셀렉션, 조인 연산 각각의 비용을 추정하는 것이다.)
또한 CPU 시간과 I/O 비용 역시 함께 고려한다.
질의 계획을 고를 때는 질의를 수행하는데 필요한 공간도 함께 고려한다.
이 공간을 plan space 라고 부르는데, 이 공간이 너무 많이 필요한 경우도 좋지 않다.
plan space 를 줄이려면 데카르트 곱을 피하는 것이 좋으며, 하나의 연산을 수행한 결과를 임시로 저장하지 않고 그 다음 연산의 input 으로 곧바로 내보내는 pipeline 식 수행을 통해 비용을 줄일 수 있다.
만약 단항 연산자 (셀렉션 또는 프로젝션) 에 대해 pipeline 이 적용되는 경우에는 연산자가 즉시 적용되었다고 해서 on-the-fly 라고 말한다.
반대로 pipeline 없이 연산 결과를 임시 테이블을 만들어 저장하는 것을 가리켜 '실체화한다 = materialize' 고 표현한다.
임시테이블은 버퍼 메모리 공간에 데이터를 추가적으로 저장하므로 메모리 공간을 소모하지만, 실체화를 하면 그만큼 디스크를 많이 왔다갔다 하지 않아도 된다.
비용 추정 예시

이제 복잡한 관계 대수가 섞여있는 연산에 대해 비용을 추정해보자.
위와 같은 SQL을 실행할 때, 관계 대수 식으로는 다음과 같이 적을 수 있다.
π_sname (σ_bid=100^rating>5 (Reserves ⨝_sid Sailors))
이 수식은 다음과 같이 관계 대수 연산자 트리로 표현할 수 있다.
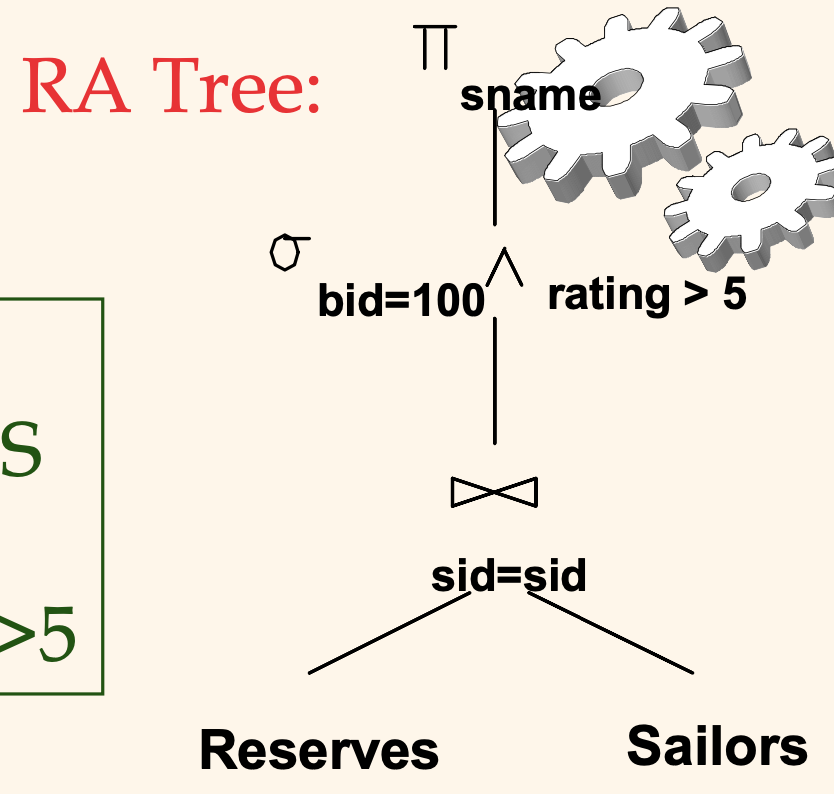
위 수식에서는 두 테이블의 자연 조인을 구하고, selection을 취한 뒤, 마지막에 projection을 수행한다.
완전한 질의 처리 계획을 얻으려면, 이 각각의 join, selection, projection 연산을 어떻게 구현할 지 결정해야 한다.
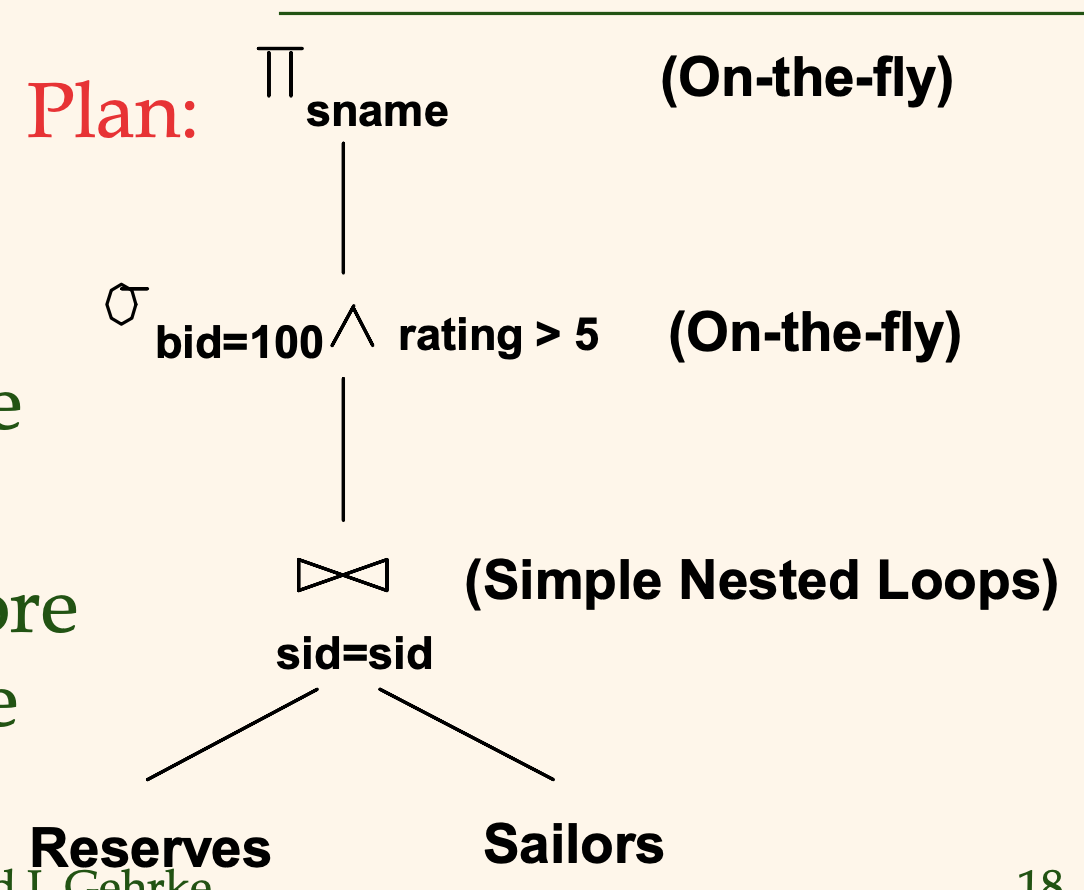
다음 그림은 질의 계획 중 하나를 나타낸 모습이다.
두 테이블의 조인 연산은 단순히 중첩 루프를 통해 구현하고,
selection 연산과 projection 연산을 수행할 때는 join 결과로 레코드가 나올 때마다 즉시 처리해서 결과를 저장하도록 하고 있다.
이 질의 계획의 수행 비용은 1000 페이지의 Reserves 데이터를 가져오고, 각각의 페이지마다 500개 페이지의 Sailors 데이터를 불러와 join 연산을 수행하므로 1000 + 1000*500 = 501000 의 비용이 든다.
(책에서는 트리의 왼쪽에 있는 노드가 outer loop에 해당하는 테이블로 본다.)
(책에서는 501000 인데 강의록에서는 500 + 1000*500 으로 계산하였다.. 왜지.. 나도 1000을 더하는게 맞다고 본다.)
이제 2가지 대안 계획을 고려하면서 이 비용을 줄여보자.
대안 계획 1 : Selection을 먼저 수행하고 join 하기
우선 join 비용이 큰 이유는 join 대상이 되는 테이블 각각의 레코드 수가 너무 많기 때문이다.
이 레코드 수를 먼저 줄이고 조인한다면 질의 수행 비용을 줄일 수 있지 않을까?
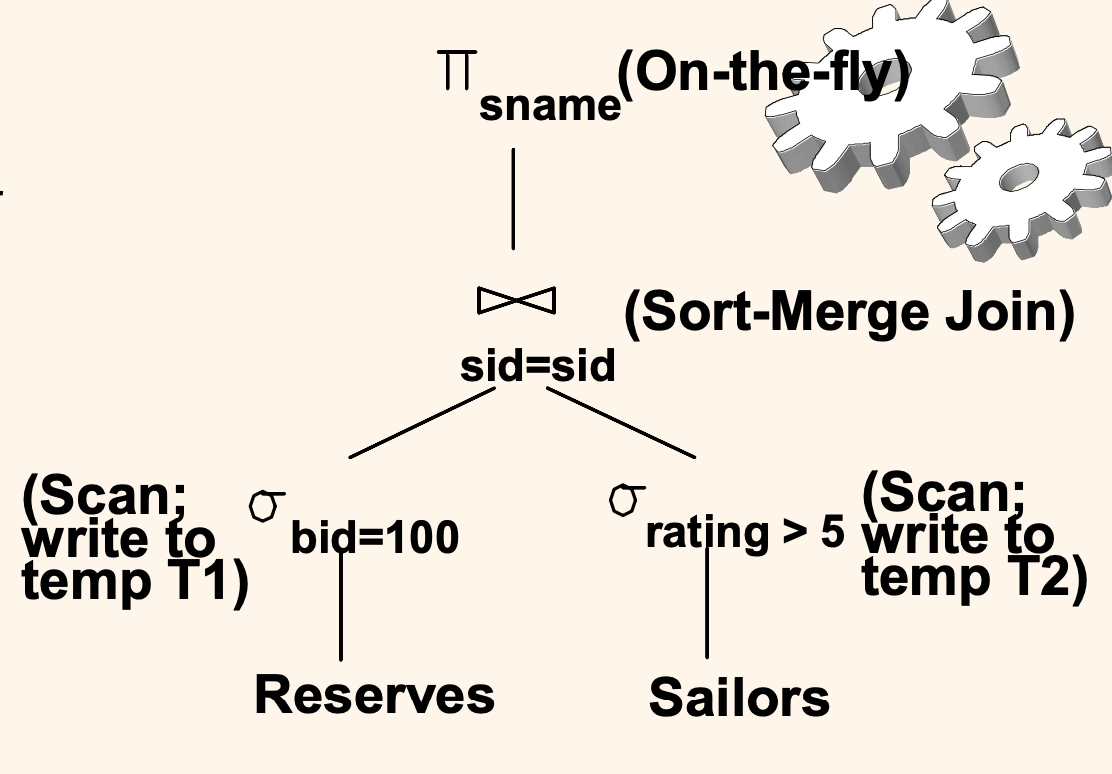
이를 고려한 대안 계획은 위와 같다.
먼저 Reserves 테이블에 대해 bid = 100 selection 을 먼저 걸고, 그 결과를 T1 테이블에 임시로 저장한다. (실체화)
다음으로 Sailors 테이블에 대해 rating > 5 selection 을 먼저 걸고, 그 결과를 T2 테이블에 임시로 저장한다. (실체화)
이 과정에서는 두 테이블을 모두 full scan 하면서 selection 조건에 부합하는지 확인할 것이다.
그 다음으로 T1, T2 에 대해 join 할 때는 Srot-Merge join 방식으로 구현한다고 해보자.
마지막으로 이 결과에 대해서 sname 을 뽑아내는 것은 join 결과가 하나 나올 때마다 즉시 처리할 수 있으므로 on-the-fly 방식으로 임시 테이블을 거치지 않고 처리한다.
이 대안 계획의 비용은 다음과 같다.
1. bid = 100 을 선별하는 비용
만약 100개의 보트가 있고 그 보트가 균등하게 예약되었다면, 10만개 예약 데이터 중 1000개 데이터를 선별할 것이다.
(데이터의 분포를 파악하기 위해 쿼리 플랜 비용을 추정할 때 샘플링을 할 수도 있다. Explain 글에서 참고)
Reserves 테이블을 full scan 할 때 1000개 페이지를 가져오고, 순회 결과를 T1 테이블로 쓸 때 1000 개 데이터를 쓰므로 10개 페이지를 쓰게 된다. (T1을 디스크에 저장)
비용 : 1000 + 10 = 1010
2. rating > 5 를 선별하는 비용
만약 10개의 rating 이 있고, 각 선원의 rating 분포가 균등하다면 rating > 5 인 선원은 대략 절반정도 있을 것이므로 250 페이지에 걸쳐 존재할 것이다.
따라서 Sailors 테이블을 full scan 할 때 500 개 페이지를 읽어오고, T2를 쓸 때는 250 페이지를 쓴다. (T2를 디스크에 저장)
비용 : 500 + 250 = 750
3. T1, T2 를 sort-merge join 하는 비용
다음 글에서 정리하겠지만, 외부 정렬시 5개 버퍼가 있다면, 10개 페이지를 정렬 할 때는 log_4 (10) = 대략 2번의 패스가 필요하다.
250개 페이지를 정렬할 때는 log_4 (250) = 대략 4번의 패스가 필요하다.
따라서 T1을 정렬하는 비용은, 2 * 2 * 10 = 40, T2를 정렬하는 비용은 2 * 4 * 250 = 2000
각각의 정렬 결과를 모두 순회하면서 합치는데 10 + 250 = 260 의 비용이 든다.
비용 : 40 + 2000 + 260 = 2300
최종적으로 위의 1, 2, 3 비용을 모두 더하면 1010 + 750 + 2300 = 4060 페이지의 입출력 비용이 발생한다.
+ 책에서 자세한 알고리즘을 소개하진 않았지만, 블록 중첩루프 조인을 사용하여 조인을 구현하면 10 + 4*250 = 1010 의 비용으로 조인 연산을 수행할 수 있어 1 + 2 + (블록 중첩루프 조인 비용) = 2770 의 비용으로 이 질의를 수행할 수 있다고 한다.
+ 조인하기전에 셀렉션 연산을 먼저 수행한 것처럼, 만약 조인하기 전에 projection 연산을 먼저 수행하면 T1, T2 테이블의 크기를 줄일 수 있으므로 조인 비용이 250번 이하로 줄어들어 총 비용이 1010 + 750 + 250 = 2010 이하로 줄어든다고 한다.
이 내용 역시 구체적인 설명은 없었다..
대안 계획 2 : 인덱스 이용하기
만약 Reserves 테이블에 대해 bid 필드에 인덱스가 걸려있다면 어떨까?
위에서 인덱스 중첩 루프는 특정 조건에 의해 outer loop 크기가 작아지는 경우 연산량이 줄어든다고 했던 내용과 연계해서 이해해보자.
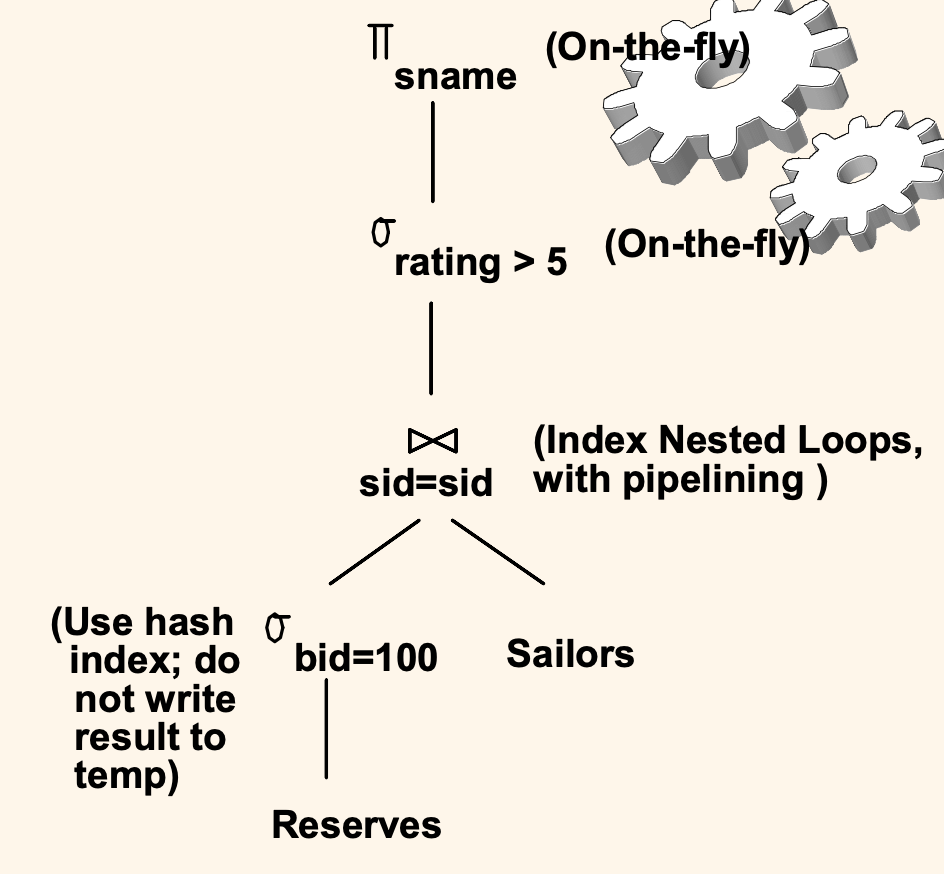
이번엔 위와 같이 질의 계획을 만들 수 있을 것이다.
먼저 Reserves 테이블에 대해 bid = 100 조건을 먼저 처리한다.
bid 에만 인덱스가 걸려있고, 이 인덱스가 해시 기반 군집 인덱스라고 해보자.
이 연산의 결과는 별도의 임시 테이블 없이 파이프라인 방식으로 곧바로 올려서 Index Nested Loop 방식으로 조인하여 조인 연산을 처리한다고 해보자.
(Reserves 테이블이 outer, Sailors 테이블이 inner 이고, index nested loop 는 인덱스가 걸린 테이블이 inner 로 들어가므로 Sailors 에도 sid에 index 가 걸려있다는 것을 유추할 수 있다. 이때 sid는 PK 라서 최대 한 개의 레코드만 가지므로 비군집 인덱스여도 상관없다.)
이 질의의 추정 비용은 아래와 같이 계산할 수 있다.
1. Reserves 테이블에서 bid = 100 을 선택하는 비용
마찬가지로 bid 가 100개 보트에 대해 균등하다면 10만개 예약 데이터 중 bid = 100 보트에 대한 예약은 1000건이므로, 10개 페이지에 대해 데이터를 뽑아낼 것이다.
그 비용은 군집 인덱스라면 1.2번의 해시 인덱스 페이지를 가져온 이후, 해당 인덱스 페이지 정보를 기반으로 10개의 페이지를 읽어오면 된다.
이때 reserves 테이블에서 가져오는 데이터는 파이프라인 방식으로 가져와서 실체화 되지 않기 때문에 projection 연산을 미리 수행할 필요가 없다.
2. 각 페이지를 읽어올 때마다 Sailors 테이블과 join 연산 수행 (파이프라인)
이제 10개 페이지에 들어있는 1000개의 bid = 100 레코드에 대해, sid 가 같은 sailors 를 찾는 비용은 평균 1.2번의 해시 인덱스 페이지를 가져온 후, 그 페이지로부터 하나의 실제 데이터가 들어있는 페이지를 추가로 가져와야 하므로 1.2번의 페이지 로딩 비용이 발생한다.
따라서 1000 * 1.2 = 1200 번의 페이지 로딩이 발생한다.
(데이터 구성법 (1)을 사용하면 1.2번, 구성법 (2) (3)을 사용하면 2.2번의 비용이라는데, 구성법(1~3)이 뭘까.. 정적 해싱, 동적 해싱 2가지를 말하는 걸까? => 단순하게 정적해싱을 사용한다고 가정하면, bid = 100 인 데이터를 오버플로우 페이지에 저장한다. 평균적으로 1.2 페이지의 비용이 발생하는 것은 데이터가 균등하게 분포된 경우 오버플로우 페이지가 1개 ~ 2개이기 때문이다. 그런데 위 경우 bid = 100 인 데이터가 10페이지에 걸쳐 줄줄이 오버플로우 페이지로 딸려있는 상황을 생각하면 된다. 따라서 버켓을 찾은 뒤 10페이지를 즉각적으로 가져오면 된다. 이때 버켓은 데이터 구성법 (1~3) 을 가질 수 있는데, 책에 보면 인덱스에 데이터 엔트리로 저장하는 3가지 방법을 소개한다.
1. 데이터 엔트리는 실제 데이터 레코드인 경우 2. 데이터 엔트리는 탐색키와 rid 값 하나를 가지는 경우 3. 데이터 엔트리는 탐색키와 rid 값 리스트를 갖는 경우. 위 예시는 1번, 데이터 엔트리가 실제 데이터 레코드인 경우를 가정하였기 때문에 인덱스에서 페이지를 가져온 즉시 나머지 데이터도 알 수 있었다. 책 258페이지를 참고)
이때 rating > 5를 미리 수행하지 않은 이유는 rating 에 인덱스가 걸려있지 않으면 셀렉션 과정에서 전체 테이블을 스캔하는 과정이 추가적으로 필요하기 때문이며, 만약 rating 에 인덱스가 걸려있다면 sid 조건 하나에 대해 해시 인덱스를 쓸 수 없다.
해시 인덱스는 모든 인덱스 탐색키에 대해 동등 조건을 걸어야 쓸 수 있기 때문이다.
따라서 위 2개 연산을 합치면 1210 번의 페이지 I/O 비용이 발생한다.
만약 Sailors 테이블의 sid 가 군집 인덱스라면, bid = 100 실렉션 연산을 임시 테이블에 실체화 시키고 sid 기준 정렬한다.
임시테이블의 크기는 10페이지 이므로 5개 버퍼를 활용한 정렬비용은 2 * 2 * 10 = 40 이다.
만약 어떤 선원이 이 배를 여러번 예약했다면 sid 가 반복적으로 등장하므로 한번 sailors를 찾은 후에는 동일한 sid 에 대해 버퍼 풀에서 찾으면 비용을 줄일 수 있다.
먼저 reserves 테이블에서 군집 해시 인덱스를 사용하여 10 페이지의 데이터를 가져왔다고 해보자.
그리고 이를 2*2*10 = 40의 비용으로 sid기준 정렬했다고 해보자.
다시 테이블로 실체화하면 10 페이지의 쓰기가 발생하므로 총 60페이지의 비용이 발생한다.
다시 정렬된 sid 에 대해 정렬된 페이지 10페이지를 불러온다.
이번에는 sid가 정렬되어 있으므로 1000개 튜플을 모두 확인할 필요 없이, 내가 처음 확인하는 sid에 대해서만 확인해서 Sailors 테이블에서 해시 인덱스를 통해 평균 1.2번의 페이지 입출력으로 데이터를 가져오면 된다.
(만약 1000개 튜플들에 평균 10번씩 중복되어있다고 해보면, 100가지 sid 의 값을 가져와야 하므로 100*1.2 와 같은 식으로 계산할 수 있다. 책에서는 중복 정도에 대한 언급은 없었다.)
여기에 projection까지 미리해주면 비용을 더 줄일 수 있다.
먼저 Reserves 테이블에서 군집 해시 인덱스를 사용하여 10페이지 데이터를 가져온다.
이 데이터에서 다른 정보를 모두 제외하고 sid만 골라서 저장한다.
이 경우 레코드 하나의 크기가 감소해서(아니면 중복 sid가 없어져서?, 수업에서는 sid가 중복된 것들이 여러개 딸려 나온다고 설명하셨는데, 프로젝션은 중복을 제거하지 않나?) 3페이지에 1000튜플 정보를 저장할 수 있다고 해보고, 3페이지를 디스크에 쓴다.
조인을 하기 위해서 3페이지에 걸친 sid 데이터를 다시 가져온다. 이때 DBMS의 버퍼 페이지가 5개이므로, 3개 페이지에 걸친 데이터는 메모리 내에서 한번에 정렬할 수 있다. 따라서 정렬을 마칠 때까지 비용은 10 + 3 + 3 = 16페이지 이다.
그리고 정렬된 sid에 대해 마찬가지로 Sailors 테이블에서 데이터를 조회하면 위와 같은 이유로 모든 sid가 아니라 중복되지 않은 sid 가짓수 만큼만 찾으면 되므로 비용을 줄일 수 있다.
즉 비교해보면 다음과 같이 비용을 줄였다.
1210 페이지 → 60페이지 + 알파 → 16페이지 + 알파
'CS > 기초데이터베이스' 카테고리의 다른 글
| [데이터베이스] 23. Postgresql Explain (0) | 2024.12.05 |
|---|---|
| [데이터베이스] 22. 외부 정렬 (0) | 2024.11.29 |
| [데이터베이스] 20. 해시 기반 인덱스 (0) | 2024.11.22 |
| [데이터베이스] 19. 트리 기반 인덱스 (B+트리) (1) | 2024.10.22 |
| [데이터베이스] 18. 파일과 인덱스 (레코드 저장 방법) (0) | 2024.10.22 |
