scan conversion 은 rasterization 과 같은 말이다.
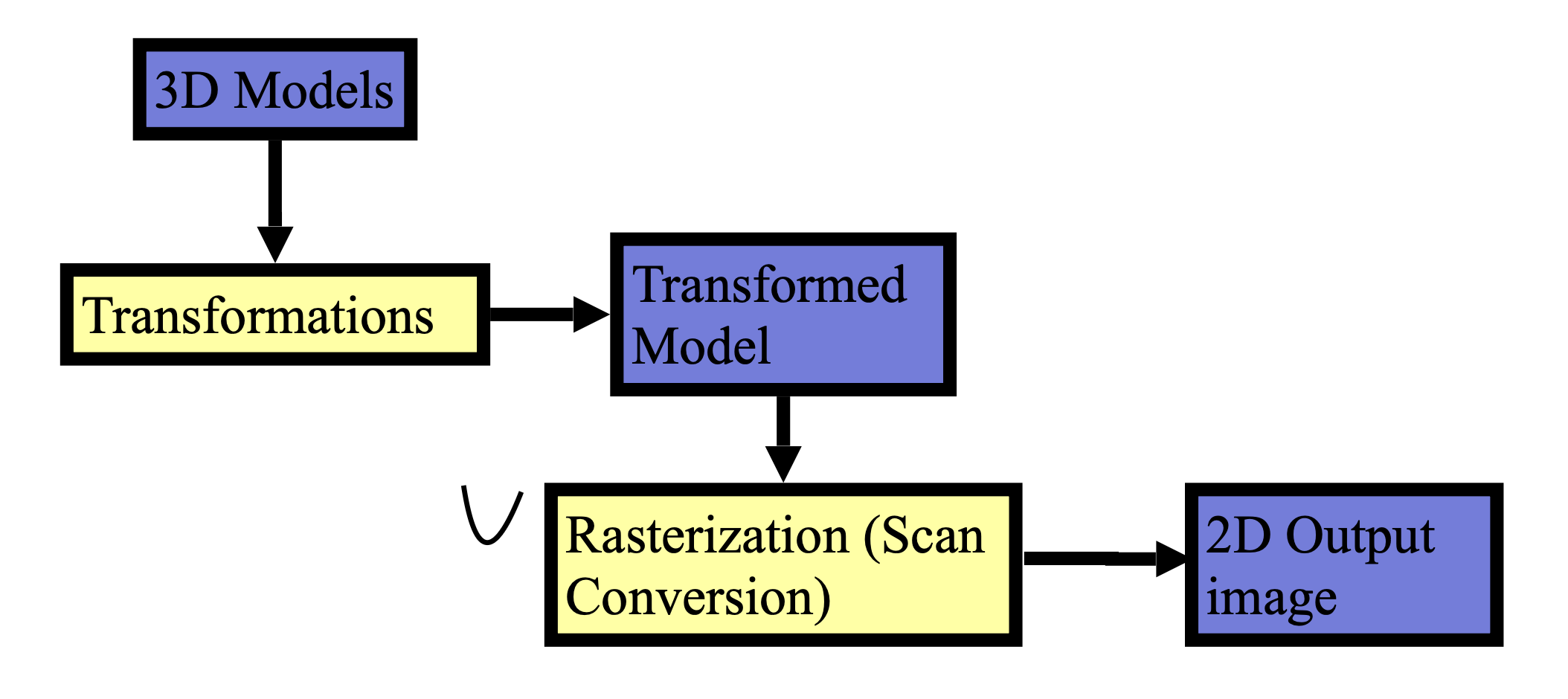
그래픽스 파이프라인을 보면 3차원 좌표계에 모델링 된 3D 물체가 있다.
이 좌표계에는 물체의 각 정점, 정점의 텍스처 값, 면을 구성하는 꼭짓점 값 등의 정보가 있다.
이제 이 모델을 2D 화면에서 보는 것과 같아지고도록 좌표변환을 거치면, 각 정점의 2D 이미지상 위치를 얻게 된다.
아직까지는 이미지에서 정점만 찍혀있기 때문에, 이제 정점을 연결하고 면 내부를 채워야한다.
이 과정이 Rasterization (scan conversion) 단계이다.
이 단계를 거치고나면 최종적으로 화면에 보여질 2D 이미지가 완성된다.
Scan Converting Line
먼저 정점이 있을 때 정점을 잇는 선부터 그어보자.
선은 그냥 그으면 되는 것 아닌가? 하고 생각할 수 있겠지만, 디스플레이의 해상도 제한 때문에 격자 무늬 픽셀 중에서 선을 표현할 픽셀을 선택해야 한다.

선을 그을 때 고려할 점은 선택된 픽셀이 끊어지지 않는 형태이며 (continuous appearance), 굵기가 일정하고, 계산량이 적어야 한다.
굵기를 일정하게 유지하면서 선을 긋는 제일 간단한 방법은, 시작점으로부터 x 좌표를 한칸씩 옮기면서 실제 선(하늘색)과 가장 가까운 픽셀을 선택하여 칠하는 방법일 것이다.
이를 슈도코드로 나타내면 다음과 같다.
void drawLine(int x0, int y0, int x1, int y1) {
double dx = x1 - x0, dy = y1 - y0;
double m = dy/dx; // 기울기
for (int x = x0, double y = y0; x <= x1; x++) {
drawPixel(x, round(y), color(x, y));
y += m;
}
}
두 점 좌표를 이용해서 기울기를 구하고,
시작점의 x좌표부터 x를 1씩 증가한 뒤, y좌표는 기울기만큼 증가시켜서 실제 하늘색 선의 위치를 찾는다.
그리고 round() 함수를 사용해서 제일 가까운 정수 픽셀을 찾는다.
하지만 이 코드에는 몇 가지 문제가 있다.
먼저 기울기가 1이하 여야만 한다.
기울기가 1을 넘으면 y좌표가 듬성듬성 찍히기 때문에 연속적인 픽셀을 그릴 수 없기 때문이다.
이때는 x, y 좌표의 역할을 바꿔서 수행한다. (이 경우 y 기준으로는 기울기가 1보다 작아지므로)
또한 기울기가 0이거나 무한대인 케이스도 고려해야한다.
그리고 사실 이 방법은 계산량이 많은 편이다.
실수형 변수를 사용하고 있고, round() 함수도 연산량이 많기 때문이다.
실제로 정수만 사용해서 선을 그리는 알고리즘도 있다.
Z-Buffer Algorithm
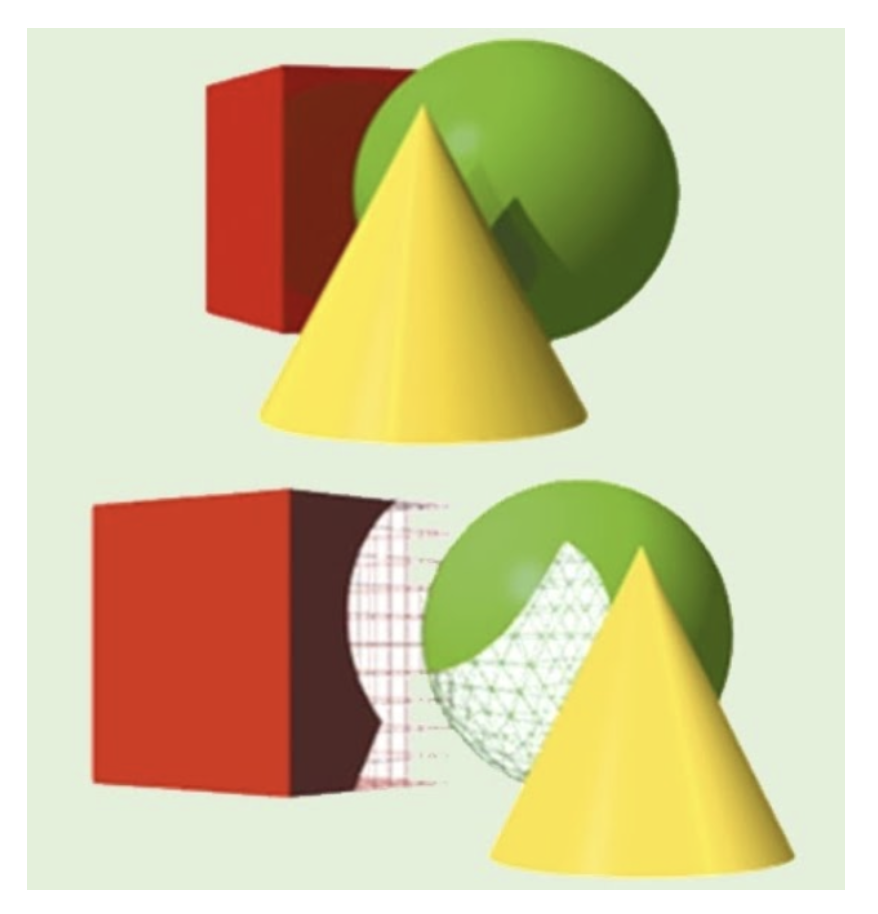
이제 폴리곤에 대해 스캔 컨버전을 진행하기에 앞서 Z-Buffer 알고리즘을 정리해보자.
이 알고리즘은 위 그림처럼 여러 물체가 겹쳐있을 때, 어떤 부분이 보이고, 어떤 부분이 숨겨지는지를 결정하는 문제(visible surfice determination)에서 활용된다.
ray tracing 을 사용하면 시각 광선이 제일 처음 부딪히는 물체만 보게 되므로, 이 문제가 자연스럽게 해결되지만
ray tracing 을 사용하지 않고 렌더링하는 경우에는 이 물체가 앞에 있는 물체인지 뒤에 있는 물체인지 알 수 없기 때문이다.
렌더링을 할 때는 object centric / image centric 방식으로 나뉘는데,
ray tracing 은 image centric 방식이고, scan conversion 은 object centric 방식이다.
ray tracing 은 이미지를 중심으로 각 좌표마다 물체가 있는 쪽으로 광선을 쏴서 픽셀을 계산한다면
rasterization (scan conversion) 은 물체에서 이미지쪽으로 정사영해서 픽셀값을 계산하는 방식이다.
이 과정을 각 물체마다 반복하기 때문에, 한번 정사영을 하고 나면 어떤 물체가 앞에 있고 뒤에 있는지를 알 수 없다.
이때 사용하는 것이 바로 Z-Buffer 알고리즘이다.
Z-Buffer 알고리즘은 말 그대로 물체와 카메라 사이의 거리(Z좌표 값)를 버퍼에 저장하는 것이다.
z축은 카메라에서 바라보는 시점 기준으로 앞 / 뒤를 나타내는 축이기 때문이다.
이때 z 좌표값은 NDC (normalized device coordinate, 디스플레이 해상도에 상관없이 -1 ~ 1 사이의 값으로 정규화된 좌표계) 에서의 z 값을 말한다.
z 버퍼에는 지금까지 렌더링한 물체의 z 좌표중 가장 가까웠던 물체의 z 좌표를 저장하는 간단한 알고리즘이고,
이미지의 각 픽셀마다 z 값을 저장해야 하므로 이미지 해상도만큼의 2차원 배열 형태로 z값을 저장한다.

이때 z 값을 저장하는 범위는 위와 같다.
무작정 크다고 다 저장하는게 아니라, 너무 가까우면 또 시야에서 안 보이기 때문에 초기값은 제일 멀리 있는 위치값으로 세팅해두고 Front clipping plane 위치에 있는 z 값까지만 저장한다.
Z-Buffer 알고리즘의 슈도코드는 다음과 같다.
void ZBufferAlgorithm()
{
int x, y ;
for each pixel (x, y) on Screen
z_buffer (x, y) = INIT_Z ; // initialize Z-buffer: scalar
set_pixel(x, y, INIT_COLOR); // initialize color: 3D vector
for each polygon P
for each pixel (x, y) in P
compute z_depth at x, y
if z_depth > z_buffer (x, y) then
set_pixel (x, y, color)
z_buffer (x, y) = z_depth
}
먼저 z_buffer 를 back-clipping palne 의 z값으로 초기화하고, 픽셀의 색상값도 초기 색상값 (r, g, b) 로 설정한다.
이제 각 폴리곤을 순회하면서 폴리곤의 각 픽셀마다 z 값을 계산한다.
z 값은 모두 음수이고, 작아질수록 멀어지고, 커질수록 가까워지므로
이 값이 현재 버퍼에 있는 값보다 크다면 현재 이미지의 픽셀 값을 해당 폴리곤의 색상 값으로 그리고, z_buffer를 업데이트한다.
폴리곤 안의 z 값을 계산할 때, 우리는 정점의 z 값만 알고 있기 때문에 각 정점을 기반으로 평면 방정식을 세워서 계산한다.
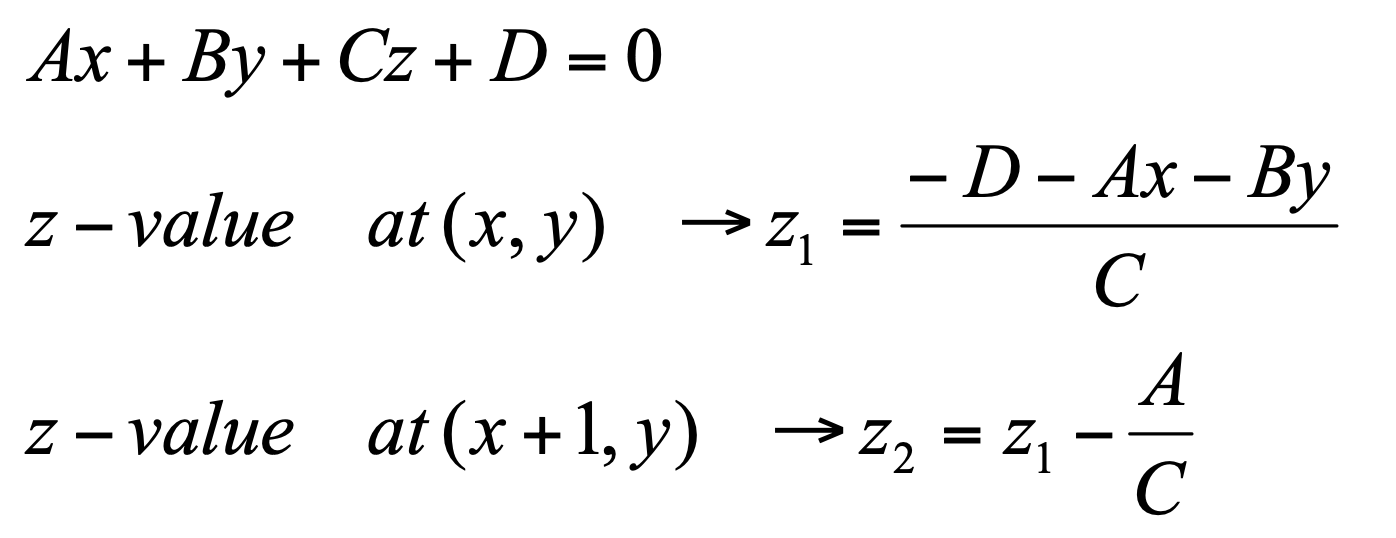
따라서 임의의 z 값은 폴리곤에 대해 구한 평면 방정식에 (x, y) 값을 대입하고 z 에 대해서 풀면 된다.
이때 x 값이 1 증가할 때마다 z 값은 A/C 만큼 감소한다.
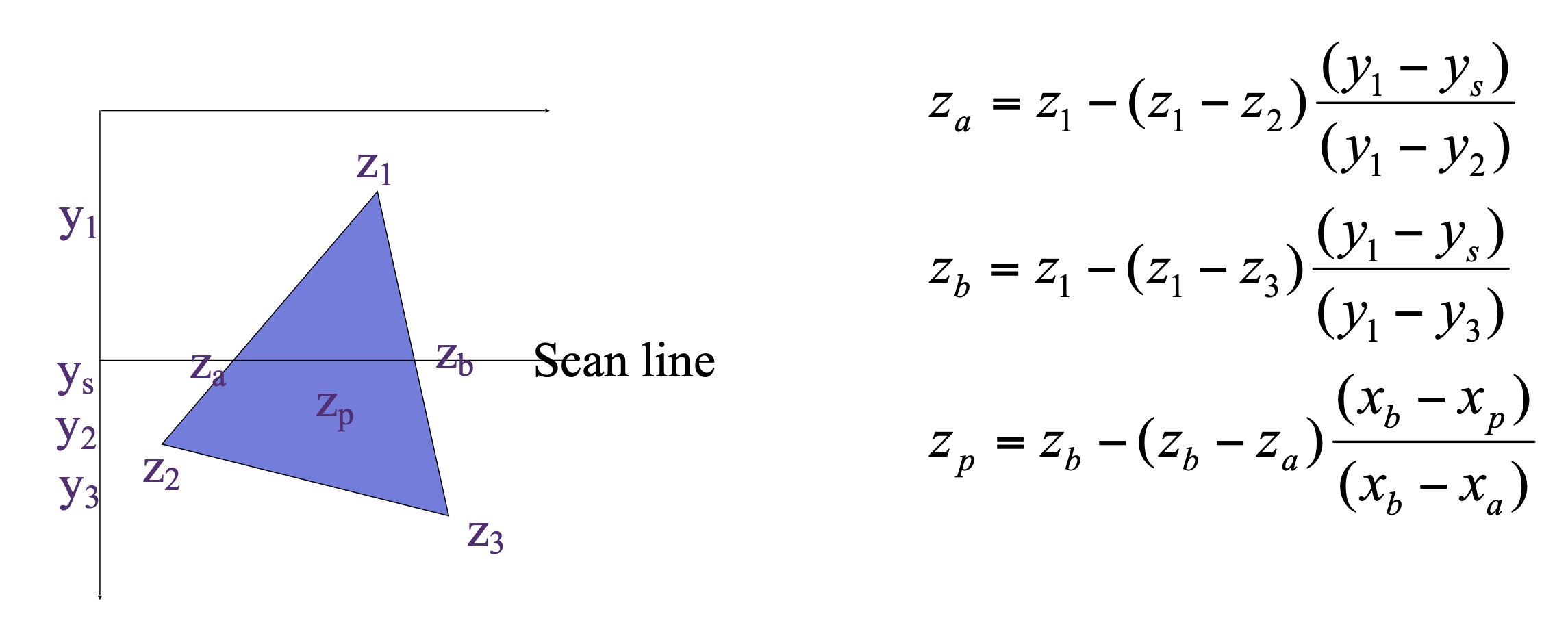
이 성질을 이용하면 매번 평면 방정식을 계산하지 않고도
이렇게 선형 보간을 통해서 모든 폴리곤 점마다 z 값을 계산할 수 있다.
Z-Buffer 알고리즘은 간단하고 계산이 빠르며, 하드웨어로 구현도 쉽다는 장점이 있다.
하드웨어로 구현이 쉽다는 것은 메모리만 있으면 된다는 말이다.
Z-Buffer 의 크기는 1byte 로 하면 다양한 깊이를 표현하는데 부족할 수 있어서 보통 2byte 로 설정하며 (이것도 부족할 때가 있다)
이 값이 이미지 해상도만큼 다 필요하므로 이미지 가로 x 세로 x 2byte 만큼의 메모리 공간이 필요하다.
사실 그렇게 큰 메모리가 필요한 것이 아니라서 하드웨어의 부담이 적다는 뜻이다.
하지만 결국 추가적인 메모리가 필요하며, 보이지 않는 물체도 함께 계산하기 때문에 불필요한 연산이 많다는 단점이 있다.
Polygon
이제 폴리곤에 대해서 scan conversion 을 수행해보자.
폴리곤에 대해서 scan conversion 을 한다는 것은, 폴리곤의 정점 3개 또는 4개를 기반으로 그 안에 있는 픽셀값을 계산하는 과정이다.
스캔 컨버전 과정에서는 z값 계산, 색상값 계산 뿐만 아니라 퐁 셰이딩을 적용한다면 법선 벡터의 보간을 계산하는 과정도 들어간다.
이 외에도 illumination, shading 처리도 이때 수행한다.
폴리곤에 대해 scan conversion 을 수행하는 제일 간단한 알고리즘은 브루트포스 알고리즘이다.
이 방식은 모든 물체가 볼록 다각형 (convex) 라고 가정하고 사용하는 방법이며, 브루트포스이기 때문에 효율적이진 않다.
(오목한 부분이 있다면 물체를 볼록 다각형으로 쪼개서 생각하면 된다)
For each polygon
1. Find the min and max Y by looping through all the polygon vertex
2. for each scanline y=j in [minY, maxY]
for each edge (p0,p1) of the polygon
calculate the scan edge intersection:
find t satisfying (p=p0+t(p1-p0) and y=j)
compute xLeft and xRight
3. for x = xLeft to xRight
compute Z, color
update Z-buffer and color-buffer if necessary
알고리즘을 슈도코드로 간단하게 나타내면 위와 같다.
먼저 모든 폴리곤에 대해 반복해서 수행해야 한다.

1. 폴리곤을 구성하는 모든 정점의 y 좌표 최소, 최댓값을 찾는다.
2. y좌표의 최소부터 최대를 향해 순회하면서 , 모든 edge 를 찾는다.
edge 를 찾을 때는 y = j 라는 현재 scan line 과 p=p0 + t 라는 두 정점으로 구성된 직선의 방정식 사이 교점을 이루는 t 값을 쭉 구하는 과정이다.
이렇게 scan line 과 edge 의 교점을 구하면, 좌우 교점을 알 수 있다. (위 그림에서 j 선과 edge 2개로 만들어지는 교점 2개)
3. 이 좌우 교점을 범위로하여 가로로 순회하면서 폴리곤 내부 점에 대해 z 값과 색상을 계산하고, z-buffer 를 업데이트한다.
'CS > 컴퓨터그래픽스와 메타버스' 카테고리의 다른 글
| [그래픽스] 8. Transformation (0) | 2025.06.11 |
|---|---|
| [그래픽스] 7. Bilnn-Phong illumination model (3) | 2025.06.11 |
| [그래픽스] 5. Rendering (3) - Lightening & Ray Tracing (0) | 2025.06.09 |
| [그래픽스] 4. Rendering (2) - Texture Mapping, Shadow Generation (1) | 2025.06.08 |
| [그래픽스] 3. Rendering (1) - Shading (0) | 2025.06.08 |
