
렌더링은 빛과 물체가 있을 때, 관찰자가 현재 물체를 어떻게 보는지를 그려내는 과정이다.
3D 모델을 화면에 표시하는 과정은 크게 위와 같다.
이번 글부터는 위 단계 중 Lighting 과 Shading 단계를 자세히 살펴본다.
Lightening 은 illumination 이라고도 부르며,
물체가 빛을 받았을 때, 그 물체의 정점의 색이 어떻게 되는지를 계산하는 과정이다.
Shading 은 결정된 정점 색을 기준으로 물체 내부에 색을 입히는 과정이다.
(폴리곤의 내부 픽셀 각각의 색을 결정하는 과정)
폴리곤 메시 형태의 모델에 대해 색을 입히는 Polygon Mesh Shading 은 기본적으로 각 폴리곤 면마다 lighting 모델을 적용하여 색을 결정한다.
그리고 구체적인 방법에 따라 크게 Flat Shading, Gouraud Shading, Phong Shading 이 있다.

각 방법별 셰이딩 적용 결과를 먼저 보면 위와 같이 보인다.
셰이딩을 적용하지 않으면 물체의 모든 면을 단색으로 처리한다.
이렇게 하면 비사실적으로 보이고, 물체가 2차원처럼 보이게 된다.
Flat Shading

interpolation(보간) 을 적용하지 않는 기법으로,
각 메시의 면마다 illumination model 을 적용하여 각 면을 동일한 광도로 처리하는 것을 말한다.
각 면을 하나의 색으로 채우기 때문에 면과 면 사이의 경계가 두드러지게 보여서 곡면이 곡면처럼 보이지 않게 되는 단점이 있다.
한 점에서의 밝기 값(색상 값)을 계산할 때는 빛의 위치, 관찰자의 위치, 면이 향하는 각도 3가지를 고려해야 한다.
어떤 면이 가장 밝게 보일 때는, 빛이 점광원이라고 했을 때 광선 벡터와 법선 벡터가 일치할 때 제일 밝게 보인다.
면이 향하는 각도는 각 면의 normal vector 로 결정하며,
polygon mesh 의 경우 normal vector 는 실제 곡면의 normal vector 근사치를 사용한다.
Flat Shading 의 장점은 계산이 적고 간단하다는 것이다.
하지만 곡면에서 사실감이 낮고, 경계면이 두드러지게 보인다는 단점이 있다.
사실감을 높이려면 polygon 을 더 잘게 쪼개야 하지만, 그럼에도 각 조각마다 경계면의 계속 보이기 때문에 여전히 한계가 있다.
Gouraud Shading
광도 보간법 (intensity interpolation) 을 사용한다.
이 방법은 꼭짓점의 법선 벡터를 이용해서 조명을 계산한 뒤,
이 값을 선형 보간해서 모서리의 조명을 계산하고
모서리 조명 값을 선형 보간해서 면의 조명을 계산하는 방법이다.
단계 별로 과정을 따라가보자.
1. 정점의 법선 벡터 구하기
우리는 각 면의 법선벡터를 알고 있다.
어떤 꼭짓점이 맞닿아있는 모든 면의 법선벡터를 평균내서 정점의 법선벡터를 구한다.
(Flat Shading 에서는 이 면의 모든 픽셀 색상을 동일한 법선벡터를 기준으로 채웠었다)

인접한 모든 면의 법선벡터를 다 더한 벡터의 단위 벡터를 구하는 것과 같다.
(지금은 모든 법선벡터를 균등하게 적용했는데, 꼭짓점과 각 법선벡터 사이 거리를 고려하여 가중치를 두는 경우도 있다)
이 과정을 모든 정점에 대해 다 수행해준다.
2. 정점의 밝기 구하기 (illumination model 적용)
각 정점 별로 ambient light, diffuse reflection, specular reflection, transparency 와 같은 값을 구한다.
3. 선형 보간
정점의 밝기 값을 기반으로 선형보간하여 모서리의 조명값을 계산한다.
그리고 모서리의 조명값을 기반으로 면의 조명값을 계산한다.
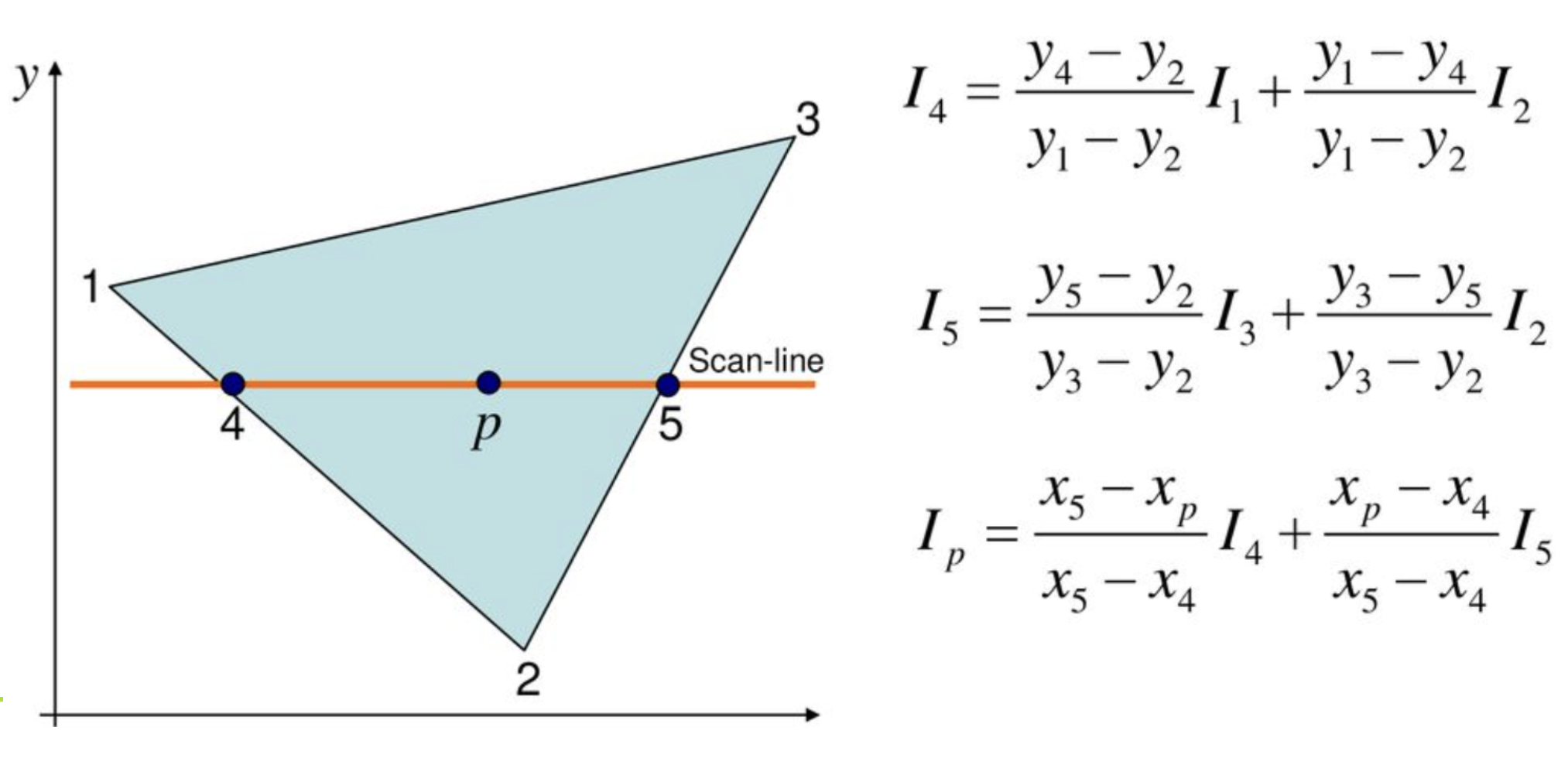
i1, i2, i3 은 정점 1, 2, 3 의 밝기 값을 갖고 있다.
Scan-line 을 따라 계산할 때, 현재 scan line 과 닿아있는 모서리 점 4, 5 의 밝기 값은
각각 (i1, i2) 의 밝기 값을 i1, i2 사이의 거리 비율에 맞게 적용하여 더한 값 i4 와
(i2, i3) 의 밝기 값을 i2, i3 사이에서 거리 비율에 맞게 적용하여 더한 값 i5 로 표현한다.
그리고 내부 면의 특정 점 p 의 밝기값은 앞서 구한 i4, i5 의 거리 비율을 기반으로 구한다.
거리 비율을 구할 때는 x, y 좌표 중 하나의 거리 비율을 선택해서 사용하면 된다. (어떤 걸 사용하든 비율은 동일하다)
예를 들어 i4 의 밝기 값은 i1, i2 의 밝기 값이 특정 비율로 섞여서 결정된다.
그 섞이는 비율을 거리를 기반으로 비례식을 세워보면
i1 : i2 = p1p4 : p4p2
i2 * p1p4 = i1 * p4p2
p1p4 는 p1p2 에서 p1p4 의 길이 비율, p4p2 는 p1p2 에서 p4p2 의 길이 비율로 보면 된다.
이 길이 비율을 그대로 x 또는 y 를 기반으로 표현하면 i1, i2 이 어느 정도 비율로 섞이는지 알 수 있다.
그 비율을 i1, i2 에 곱해서 더해주면 i4 의 밝기 값이 된다.
Gouraud Shading 방법은 hidden surfice algorithm 과 조합하여 보이지 않는 면은 그리지 않는 방식으로 사용할 수 있다.
그리고 보간을 통해 밝기 값이 한번에 크게 바뀌는 문제를 해결하여 더 사실적인 셰이딩을 적용할 수 있다.

이 그림은 flat shading 과 gouraud shading 의 차이를 보여준다.
gouraud shading 방법을 사용하면 실제로는 폴리곤으로 이루어진 모델도 곡면인 것처럼 보이게 된다.
하지만 단점도 있다.
이 방법은 기본적으로 꼭짓점과 모서리의 밝기 값을 기반으로 면의 밝기를 채우는 방식이다.
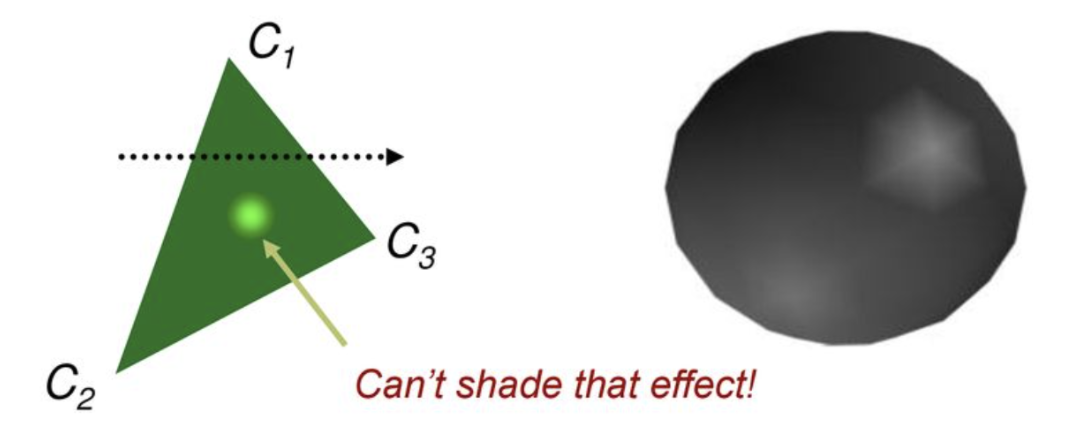
따라서 위 그림과 같이 특정 면 안에 하이라이트되는 밝기 표현은 할 수 없다.
Phong Shading
gouraud shading 이 밝기를 보간했다면
퐁 셰이딩은 법선벡터를 보간하는 방법이다.
먼저 각 정점의 법선 벡터를 선형보간하여 각 면에서의 법선벡터를 구한 뒤
이 각 면을 구성하는 각 점의 법선벡터를 기반으로 밝기 값을 구하는 방법이다.
퐁 셰이딩을 사용하면 면의 특정점에 대한 하이라이팅 효과를 잘 표현한다는 장점이 있다.
(다른 셰이딩 방법도 하이라이팅을 표현은 할 수 있다. 다만 '잘' 표현하지 못 할 뿐이다)
따라서 물체가 빛을 잘 반사히지 않는, 하이라이트가 거의 없는 물체라면 굳이 퐁 셰이딩을 적용할 필요가 없다.
퐁 셰이딩은 하이라이팅을 위해서 사용하는 방법이다.
그리고 ray tracing 과 같은 기술을 사용하지 않는 경우에도 퐁 셰이딩을 통해 셰이딩을 적용한다.
퐁 셰이딩을 적용하는 단계는 다음과 같다.
1. 정점의 법선벡터 구하기
각 면의 법선벡터를 더해서 구한다. (gouraud shading 과 동일)
2. 정점의 법선벡터를 선형 보간
3. 각 면을 구성하는 보간된 법선벡터에 대해 illumination model 적용
gouraud shading 과의 차이점을 보면 illumination model 을 꼭짓점에만 적용할 것인지
모든 면의 점에 적용할 것인지의 차이이다.
그런데 illumination model 은 삼각함수와 같이 복잡한 계산이 많이 들어간다.
따라서 퐁 셰이딩은 gouraud shading 기법에 비해 계산량이 더 많다는 단점이 있다.
(= 시간이 오래 걸린다)

정점의 법선벡터를 선형보간하는 방법은 위와 같다.
꼭짓점 1, 2 에서의 법선벡터가 N1, N2 라면,
그 거리 비율을 기반으로 모서리 위의 점 4의 N4 법선벡터를 구한다.
마찬가지로 꼭짓점 2, 3 에서의 법선벡터 N2, N3를 기반으로 이 두 점에 의한 모서리 위의 점 5의 법선벡터 N5 를 구한다.
N4, N5 의 법선벡터를 기반으로 면 내부 점 p 의 법선벡터 Np 를 구한다.
사실 방법은 gouraud shading 과 동일한데, 밝기를 보간하냐, 법선벡터를 보간하냐의 차이만 존재한다.
퐁 셰이딩도 visible surface detection (안 보이는 면은 숨기고 보이는 면만 셰이딩) 기법과 함께 사용된다.

최종적으로 3가지 셰이딩 기법을 비교해보면 위와 같다.
'CS > 컴퓨터그래픽스와 메타버스' 카테고리의 다른 글
| [그래픽스] 6. Scan Conversion (1) | 2025.06.11 |
|---|---|
| [그래픽스] 5. Rendering (3) - Lightening & Ray Tracing (0) | 2025.06.09 |
| [그래픽스] 4. Rendering (2) - Texture Mapping, Shadow Generation (1) | 2025.06.08 |
| [그래픽스] 2. Modeling (0) | 2025.06.08 |
| [그래픽스] 1. 컴퓨터 그래픽스 (8) | 2025.06.07 |
