Texture Mapping
텍스처는 물체 표면의 질감(거침, 부드러움)을 나타내는 무늬를 가진 2차원 배열 이미지를 말한다.
이 2D 이미지를 3차원 모델에 입혀서 사실감을 더해주는데 사용되며, 2D 텍스처 이미지를 3D 모델에 입히는 것을 가리켜 texture mapping 이라고 한다.
텍스처는 사람이 직접 찍거나, 스캔하는 등의 방식으로 얻어낼 수 있다.
텍스처 매핑 방법은 크게 Non-parametric 방식과 parametric 방식으로 나뉜다.
Non-parametric 방식은 배경에 이미지를 두고, 물체에 구멍을 뚫어서 구멍을 통해 보이는 배경으로 텍스처를 간접 매핑하는 방식이다.
물체가 이동, 회전해도 배경은 그대로기 때문에 자연스러운 방법은 아니다.
중요한 것은 parametric texture mapping 방식이다.
이 방식은 texture space 와 screen space 를 분리한 방식으로 (= 텍스처 좌표계와 screen 좌표계를 분리)
물체에 텍스처를 입히는 과정을 texture space 에서 진행하고, 그 결과물을 화면에 보여줄 때 screen space 에서 계산하여 보여준다.
따라서 물체가 이동, 회전하면 텍스처도 그에 맞게 바뀌어 좀 더 사실적으로 물체를 표현할 수 있다.

텍스처 이미지 좌표계는 (u, v) 또는 (s, t) 형식으로 기술한다.
그리고 이 이미지는 다양한 형태의 surface 에 wrapping 될 수 있다.
이를 위해서는 물체의 표면과 관련된 좌표계가 필요하고, 이 좌표계를 텍스처 이미지 좌표계와 매핑하는 과정이 필요하다.
만약 이 물체의 표면이 평면이라면 매핑이 쉽겠지만, 구와 같이 굴곡이 있는 경우에는 매핑이 조금 더 어려워진다.
예를 들어 구와 같은 경우에는 위도, 경도와 같은 2개의 각도를 사용하여 매핑한다.
하지만 이렇게 매핑하면 각도에 따라 어디는 간격이 넓고 어디는 간격이 좁아서 원하는대로 매핑하기가 쉽지 않다는 단점이 있다.
원기둥 형태라면 (윗면은 따로하고) 옆면만 원기둥의 높이, 수평 각도를 기반으로 매핑하면 비교적 쉽게 매핑할 수 있다.
제일 매핑하기 어려운 것은 사람 얼굴과 같이 굴곡이 많은 물체이다.
텍스처 매핑에서 중요한 개념 중 하나로는 texture resampling 이 있다.
결국 스크린에 그림을 그리기 위해서는, 현재 screen space 에 있는 물체 표면에 텍스처를 매핑해야 한다.
그러다보면 screen space 에서 그리고자 하는 물체의 각 픽셀의 색상값 (텍스처 값) 을 결정할 수 있어야 한다.
하지만 텍스처 상에서의 점을 스크린 상에서 물체의 점과 매핑할 때, 그 크기가 딱 맞지 않을 수 있다.
텍스처 좌표계를 스크린 상 물체 표면의 좌표계와 맞췄을 때, 색을 계산할 픽셀의 위치가 텍스처 상에서 중간 어딘가에 있는 픽셀을 지나는 것이다.
이런 상황에서 스크린 상 픽셀값을 결정하기 위해서 수행하는 작업이 texture resampling 이다.

이때 제일 자주 사용하는 방법이 bilinear resampling 이다.
이 방법은 결정해야 하는 픽셀을 가두고 있는 인근 4개 점의 픽셀값을 평균내서 결정할 픽셀의 색을 결정하는 방법으로,
이름 그대로 2개 방향에 대해 선형보간을 하는 방식을 사용한다.
즉, 단순히 4개의 값을 더해서 평균내는 것이 아니라, 색상을 결정할 픽셀의 위치와 인근 4개 점 위치를 기반으로 더 가까운 점의 색을 더 많이 반영하도록 거리에 비례하여 비율을 조정하여 평균을 낸다.
텍스처 매핑을 구현할 때는 Z-Buffer 알고리즘을 많이 사용한다.
이에 대해서는 뒤에서 더 자세히 정리한다.
스크린의 픽셀 색상을 결정할 때 각 픽셀의 색은 텍스처를 기반으로 결정된다.
이때 텍스처 좌표계를 찾을 때도 Gouraud 스타일의 보간 방법을 사용한다.
셰이딩에서 정리했던 방법과 마찬가지로 각 정점에서의 텍스처 좌표값을 계산하고 (색상값이 아니다)
이를 기반으로 각 정점들이 구성하는 면 안쪽의 좌표값을 거리 기반으로 보간해서 좌표값을 구하는 것이다.
좌표값을 다 구했다면, 이제 texture resampling 을 사용해서 색상을 결정하면 된다.
(결정한 좌표값은 텍스처 이미지 상에서 중간 어딘가에 애매하게 찍혀있을 가능성이 높을 것이기 때문이다)
Mip Maps
텍스처와 관련하여 mip maps 라는 개념이 있다.
우리가 물체를 보는 거리에 따라서 표현해야 할 텍스처의 해상도는 얼마든지 달라질 수 있다.
그리고 텍스처의 해상도를 한 가지만 갖고 있다면 물체의 해상도에 따라 텍스처를 입힌 결과가 이상하게 깨져보일 수 있다.
이 문제를 해결하기 위해서 사전에 하나의 텍스처에 대한 여러 해상도 이미지를 준비하는 것이다.
이를 통해 스크린 해상도와 텍스처 해상도를 비슷하게 맞춤으로서 결과가 깨지지 않도록 할 수 있다.
보통 해상도를 준비할 때는 가로, 세로 각각 1/2 씩 줄여가면서 1/4 크기의 이미지로 줄여가며 준비를 해두고,
특정 해상도 레벨을 선택할 때는 현재 물체 해상도와 비슷한 해상도 레벨 앞 뒤로 하나씩을 선정한 뒤
이 둘 사이에 선형보간을 하여 텍스처 값을 구하는 방법이 Mip Maps 이다.
Mip Maps 를 통해서 여러 해상도의 이미지를 저장하려고 할 때, 추가로 필요한 공간을 계산해보면
첫 이미지의 크기를 1이라고 하면 매번 이미지의 크기가 1/4 씩 줄어드는 무한 등비급수의 합을 구하는 것과 같으므로 4/3 이 나온다.
즉, 추가 공간이 1/3 만큼만 더 필요한 것이다.
그래서 메모리를 크게 차지하지 않는 장점이 있다.
Solid Texture
지금까지는 텍스처를 2D 이미지로만 살펴보았다.
하지만 가끔 3D 텍스처가 필요할 때가 있다.
예를 들어 어떤 물체를 자르거나, 이 물체가 깨져서 내부가 보이도록 표현하고자 한다면, 그 물체의 내부에 대한 텍스처가 함께 필요할 것이다.
이렇게 물체의 내부를 표현하는데 사용하는 텍스처가 solid texture 이다.
즉, texture 가 2차원이 아닌 3차원인 것이다.
solid texture 를 사용하는 경우, 텍스처 좌표계를 사용하여 매핑하기보다 보통 텍스처를 정의하는 함수를 계산하여 표현한다.
대표적인 예시중 하나가 Perlin Noise 함수이다.
Bump Mapping

물체의 표면이 울퉁불퉁하고 거친 경우에는 bump mapping 기법을 사용할 수 있다.
이 기법을 적용하면 위 사진처럼 벽돌과 같이 울퉁불퉁한 느낌을 줄 수 있다.
물체의 음영이라는 것은 물체 표면의 법선벡터와 빛이 들어오는 벡터의 각도 차이에 의한 밝기에 의해 표현된다.
따라서 물체가 울퉁불퉁하다는 것은 그 표면의 법선벡터와 빛의 각도가 이리저리 바뀌면서 밝기가 수시로 바뀌는 것이다.

물체의 밝기를 결정하는 blinn-phong illumination 수식을 보면 위와 같다.
여기에서 N 이 물체 표면의 법선벡터를 가리키며, R은 빛이 들어와서 정반사된 뒤 나가는 것을 가리킨다.
이 R 역시 N 벡터에 의해 바뀐다. 따라서 N 벡터의 방향을 이리저리 바꿔주면 물체가 울퉁불퉁한 느낌을 줄 수 있다.
(실제로는 평평한데 눈속임으로 울퉁불퉁하게 보이게 만드는 것)
Displacement Mapping
Bumping Mapping 이 눈속임으로 울퉁불퉁한 느낌을 표현했다면,
실제로 물체 표면의 높낮이를 바꿔서 울퉁불퉁한 느낌을 표현하는 방식이 displacement mapping 이다.
이때 물체의 높낮이를 조절할 때 흑백 texture 를 사용하여 이미지의 밝고 어두운 정도에 따라 물체의 높낮이를 조정한다.
이때 물체의 높낮이는 그 포인트의 normal vector 방향을 따라 조정한다.

이 사진을 보면 바로 이해가 된다.
이렇게 하면 실제로 높낮이가 바뀐 것이기 때문에 옆에서 봐도 높이가 달라지게 보인다.
하지만 이렇게 작업을 하려면 추가적인 전처리도 필요하고, 바뀐 높이에 따라 hidden surface 가 바뀌므로 추가적인 계산이 많이 필요하다.
보통 울퉁불퉁한 물체를 모델링할 때는 단순한 형태로 먼저 모델링한 뒤, displacement mapping 기법을 통해 디테일한 울퉁불퉁한 표현을 적용하는 방식으로 모델링한다.
Environment Mapping
다른 기법으로는 알루미늄 그릇 표면에 주변 환경이 비쳐보이듯,
주변 환경의 모습 자체를 텍스처로 하여 모델에 입히는 environment mapping 기법도 있다.
다른 물체의 모습이 반사된 모습을 가지고 매핑하기 때문에 reflection mapping 이라고도 부른다.
어떤 물체에 시각 광선을 쏘았을 때, 광선이 정반사되어 부딪히면, 그 위치의 색을 반사되었던 물체의 색으로 표현하는 것이다.
이 방법은 반사하는 물체가 하나일 때는 잘 되지만, 여러 물체가 반사하고 있다면 복잡하기 때문에 ray tracing 같은 기법을 사용한다.
이 기법은 계산량이 많다고 한다.
(4장 내용도 여기에 추가적으로 정리할 예정)
Shadow Generation
물체와 빛이 있으면 물체에 대한 그림자가 생기는 것이 자연스럽다.
그림자의 경우에는 Ray Tracing 같은 global illumination 기법을 사용하면 자연스럽게 만들어진다.
하지만 local illumination 기법을 사용하게 되면 그림자가 알아서 만들어지지 않기 때문에 직접 계산해야 한다.
그림자의 종류는 크게 2가지로 나눌 수 있다.
물체에 의해 바닥이나 벽에 생기는 projective shadow
물체 자체가 복잡해서 자신의 일부에 의해 자신에게 드리워지는 self shadow 이다.
또한 그림자는 광원의 성질에 따라 다르게 만들어지기도 한다.
햇빛과 같이 멀리 한 점에서 오는 빛 (점광원) 의 경우, 그림자가 선명하게 생기지만
강의실처럼 여러 각도에서 오는 형광등에 의해 그림자가 만들어지는 경우, 햇빛에 비해 그림자가 선명하지 않다.
이런 광원의 성질을 고려하여 그림자를 만들기 위해서 ray tracing 같은 기법을 사용한다.
(그림자를 계산하기 위한 ray tracing, rendering 을 위한 것이 아니다)
그림자를 만드는 간단한 알고리즘으로 2-pass algorithm 이 있다.
말 그대로 2개 단계를 통해 그림자를 만드는 알고리즘이다.
1-pass

shadow map 을 만든다.
빛을 물체에 쐈을 때 어디에 빛이 부딪히고 어디에 부딪히지 않는지 계산하는 과정이다.
계산 결과는 z 값을 저장하는 Z Buffer 에 저장한다.
구체적으로는 가상의 2차원 격자를 만들고, 각 격자칸을 향해 빛을 사선으로 쏜 뒤,
각 칸에서 빛이 얼만큼의 거리를 가서 부딪혔는지 그 거리 (z) 를 저장한 것이 셰도우 맵이다.
2-pass
하지만 빛과 그림자의 관계는 그냥 world 에 있는 빛과 물체만으로 결정된 데이터이다.
결국 그림자 역시 '관찰자' 에게 보여야 하기 때문에 관찰자 입장에서 그림자가 어떻게 보일지를 계산해야 한다.
이 과정을 두번째 패스에서 계산한다.
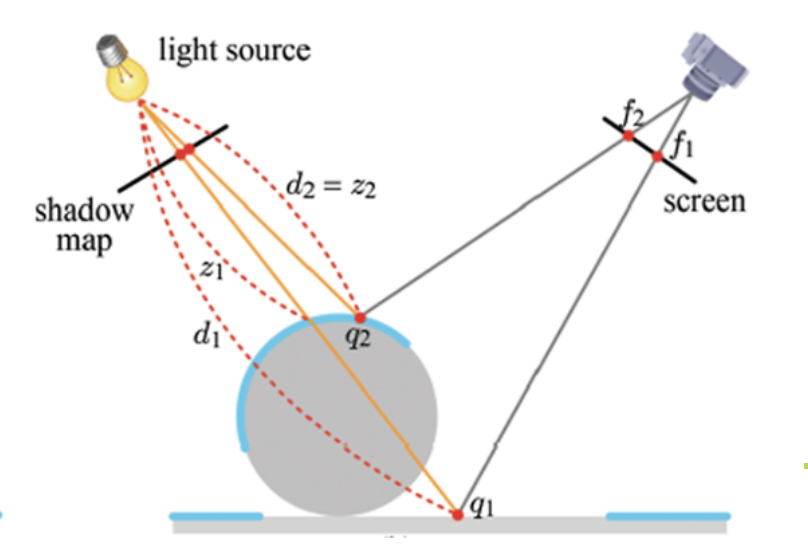
관찰자 입장에서도 스크린을 기준으로 광선을 쏜 뒤, 물체에 부딪히는 포인트를 찍는다.
이제 이 점의 색을 결정하기 위해 그 포인트와 빛 사이의 거리 d 를 잰다.
만약 이 거리 d 가 셰도우 맵에 저장했던 z 값 보다 크다면,
관찰자는 빛이 부딪힌 거리 뒤에 있는 모습을 보는 것이므로 그림자를 보게 된다. (어두운 색으로 표현)
만약 d = z 라면 빛이 부딪힌 물체의 상태를 그대로 보고 있는 것이므로 그림자가 아닌 물체를 보게 된다. (물체의 색으로 표현)
soft shadow
광원이 점광원이 아니라 area, 또는 volumn 형태일 때 그림자를 가리켜 soft shadow 라고 한다.

광원이 면적형태라면 빛이 위 그림과 같이 사방에서 날아오기 때문에 안쪽은 진한 그림자가, 바깥쪽은 옅은 그림자가 그려진다.
이런 그림자를 가리켜 soft shadow 라고 부른다.
'CS > 컴퓨터그래픽스와 메타버스' 카테고리의 다른 글
| [그래픽스] 6. Scan Conversion (1) | 2025.06.11 |
|---|---|
| [그래픽스] 5. Rendering (3) - Lightening & Ray Tracing (0) | 2025.06.09 |
| [그래픽스] 3. Rendering (1) - Shading (0) | 2025.06.08 |
| [그래픽스] 2. Modeling (0) | 2025.06.08 |
| [그래픽스] 1. 컴퓨터 그래픽스 (8) | 2025.06.07 |
