지난 글에서는 벡터와 벡터를 이용한 직선식의 표현에 대해 정리하였다.
이번 글에서는 그렇게 표현한 직선식이 여러개 있을 때, 그 직선들이 서로 만나는 지 판별하고, 만난다면 좌표를 어떻게 구할 수 있는지 그 방법을 정리하고자 한다.
2D 직선의 교점 구하기
우선 간단하게 2D 평면에 존재하는 두 직선의 교점을 구해보자.
2D 평면에서 서로 다른 두 직선은 반드시 서로 평행하거나 교차한다.
우선 두 직선이 서로 평행한 경우를 따져보자
L1: y = 2x + 1
L2: y = 2x + 3
이렇게 두 직선이 있을 때, 두 직선을 parametric 표현으로 바꾸면 아래와 같이 바꿀 수 있다.
(과정은 L1만 기록하였다)

L1(t): (t, 2t+1)
L2(t): (t, 2t+3)
저렇게 표현한 것은 사실 x = t, y = 2t+3 으로 이루어진 t를 매개로 한 식과 같다.
여기에서 x = t y = 2t+3 에 대입하면 y = 2x + 3이 나온다.
아무튼 이렇게 두 식을 구한 후, 두 식의 교점을 구해보자.
보통 문제에서는 두 식의 매개변수가 똑같이 t 로 주어질 때가 많은데,
계산을 할 때는 매개변수를 반드시 구분해서 적어야 계산의 실수를 줄인다.
두 직선은 서로 독립적이기 때문에, 같은 매개변수를 쓸 수 없다.
L1(t): (t, 2t+1)
L2(s): (s, 2s+3)
두 직선이 교차한다는 말은, 두 직선의 임의 점의 x좌표와 y 좌표가 같다는 의미이므로 아래 식을 만족하는 t, s 를 구하면 된다.
t = s
2t+1 = 2s+3
식이 2개이고 변수가 2개 이므로 해답을 판별할 수 있다.
t = s 를 두번째 식에 대입하면 2s + 1 = 2s + 3 이고, 이를 만족하는 s 는 존재하지 않는다.
따라서 두 직선의 교점은 존재하지 않으며, 두 직선이 서로 평행함을 알 수 있다.
사실, 두 직선이 평행한지는 기울기 벡터 (1, 2) 를 봄으로서도 알 수 있다.
이번엔 평행하지 않은 두 직선에 대해 교점을 구해보겠다.
과정을 위에 정리하였으므로, 과정은 간단하게 생략하겠다.

교수님이 연습을 할 때는 쉽게 답을 알 수 있는 예제를 놓고 계산 결과와 우리가 알고 있는 답이 일치 하는지 확인하라고 하셔서 정리할 때도 아주 간단한 예제를 겨져와 보았다.
두 직선 y = x + 1, y = -x + 1 의 교점은 (0, 1) 이다.
두 직선의 parametric 표현은 아래와 같이 된다.
L1(t): (t, t + 1)
L2(t): (t, -t + 1)
이제 저 방정식을 풀어보기 위해 L2 를 s에 대해 표현한 후, x좌표와 y 좌표가 같음을 식으로 세우면
t = s
t + 1 = -s + 1
이 방정식을 풀면 된다.
이 식을 정리하면
2s = 0
s = 0
t = s = 0
이때 t, s 는 x, y 를 직접적으로 의미하지 않으므로 둘 다 0 이 나왔다고 당황하지 않아도 된다.
원래 식에 이를 대입해보자.
L1(t) 에 t = 0 을 대입하면, (0, 1) 로 우리가 알고 있는 답이 나왔음을 알 수 있다.
3D 직선의 교점 구하기
위 과정을 3D에서도 똑같이 하면 된다.
3D는 교수님이 수업 중 들어주신 예제 식으로 정리하였다.
L1: y축에 평행하고, (1, 0, 0) 을 지나는 직선
L2: x축에 평행하고, (0, 1, 1) 을 지나는 직선
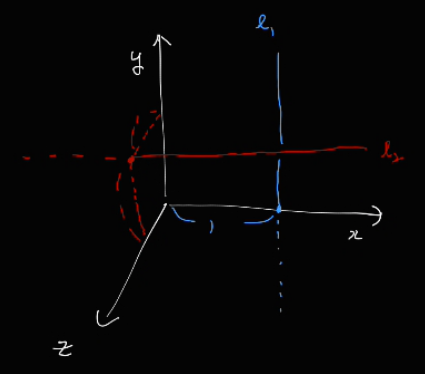
축에 평행한 직선의 경우, 기울기 벡터가 간단하므로 직선식을 아래와 같이 바로 작성할 수 있다.

L2도 축에 평행하므로 기울기 벡터가 간단하게 나온다.
따라서 이를 모두 정리하면 아래와 같다.
L1(t) : (1, t, 0)
L2(s) : (s, 1, 1)
이제 두 직선식의 x, y, z 좌표가 같다고 두고 방정식을 풀면 된다.
1 = s
t = 1
0 = 1
지금은 식이 간단하다보니 0 = 1 부분에서 교점이 존재하지 않음을 바로 알 수 있다.
하지만 연습을 위해 전체 과정을 따라 교점의 존재여부를 판별해보자.
3D평면에서는 식 3개를 한번에 다루는 것이 복잡하기 때문에, 식 2개를 골라서 본다.
변수가 2개이므로 식2개만을 다뤄도 s, t를 결정할 수 있다.
이 경우를 '그림자를 본다' 라고 한다.
예를 들어 x, y 성분 좌표만 본다고 해보자.
그러면 두 직선의 XY 평면에 생긴 그림자의 교점을 보는 것과 같다.
1 = s
t = 1
식에서 x, y 성분만 놓고 계산하면 s = 1, t = 1 일 때 교점이 생긴다.
이렇게 t, s 값을 구했다면 이 값을 전체 교점에 대입한다.
x, y 성분에서는 문제 없이 대입되어 값을 특정할 수 있지만,
z 성분에서는 어떤 값을 대입해도 0 = 1 을 만족시킬 수 없다.
이번엔 y, z 성분 좌표만 본다고 해보자.
그러면 두 직선의 YZ 평면에 생긴 그림자의 교점을 보는 것과 같다.
t = 1
0 = 1
식에서 y, z 성분만 놓고 계산하면, t = 1 로 특정이 되지만, z 성분에서 0 = 1 이므로 교점이 존재하지 않는다.
두 직선의 YZ 평면에 생긴 그림자에 교점이 없다는 의미는 두 직선의 교점이 존재하지 않음을 의미한다.
식이 복잡해지더라도 3개의 성분 중 2개를 골라 s, t 의 값을 하나로 특정할 수 있는지 확인해서 교점을 구하거나, 교점을 구할 수 없음을 보이면 된다.
이렇게 2D 와 3D에서 서로 다른 두 직선의 교점을 구하는 과정을 정리해보았다.
다음 글에서는 내적과 내적을 이용한 직선식의 표현에 대해 정리해보겠다.
'CS > 멀티미디어응용수학' 카테고리의 다른 글
| [멀티미디어응용수학] 5. 입사 벡터로부터 반사 벡터 구하기 (0) | 2023.10.17 |
|---|---|
| [멀티미디어응용수학] 4. 직선과 평면, 점 사이의 최단 거리 (0) | 2023.10.14 |
| [멀티미디어응용수학] 3. 외적과 외적의 응용 (0) | 2023.10.12 |
| [멀티미디어응용수학] 2. 내적과 내적의 응용 (0) | 2023.10.11 |
| [멀티미디어응용수학] 0. 벡터와 선분 표현 (2) | 2023.10.04 |
