지수 base convention
알고리즘에서 제일 중요한 지수의 base 는 '2' 이다.
따라서 앞으로 아래와 같은 컨벤션으로 로그를 작성한다.
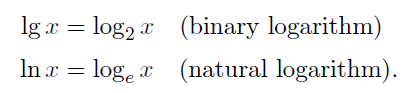
여기에 더해 log x 는 밑이 10인 로그를 의미한다.
Ceiling, Floor
만약 문맥상 반드시 정수가 와야하는데, Ceiling, Floor 기호가 빠져있다면, 어떤 나눗셈에 대해 Floor 가 적용된 것으로 본다.
“For the number of inputs n, the running time T(n) = 2T(n/2) + 1.” 라는 문장의 의미는
“ · · · , T(n) = 2T(⌊n/2⌋) + 1.” 라는 의미와 같다.
Notation

big-O 는 g(n) 이 f(n) 보다 항상 크거나 같다.
즉, g(n)이 f(n)의 최악이다.
big-Omega 는 g(n) 이 항상 f(n) 보다 작거나 같다.
즉, g(n)이 f(n)의 최선이다.
big-Theta 는 g(n) 과 f(n)이 같은 순서로 증가한다는 것을 의미한다.
이 말은 O(g(n)) 과 big-omega(g(n)) 이 모두 f(n) 과 같다는 뜻이다.
덧셈과 곱셈의 시간 복잡도
n자리 수 2개를 더할 때, 덧셈을 하는 과정을 따라가보면 각 자리수 하나하나를 더하고, carry를 발생시키고, 다시 더하고 캐리를 발생시키는 작업을 n번 반복한다.
더하고, 캐리를 발생시키는 각각의 작업은 각 1번씩 일어나며, 더하는 수의 길이에 상관없이 일정하다.
이 과정은 더하는 수의 길이 n 만큼 반복적으로 일어나므로, 덧셈의 시간복잡도는 O(n) 이다.
반면 곱셈은 피승수를 승수의 각 자리수마다 한번씩 곱한다.
한 자리수에서 곱셈을 계산할 때는, 피승수의 자리수를 승수의 특정 자리수와 한번씩 곱하고 그 결과를 더하는 과정을 반복하므로 n번의 곱셈과 덧셈 연산이 필요하다.
이 과정을 승수의 자리수 n번만큼 반복하므로, 곱셈의 시간복잡도는 O(n²) 이다.
피보나치 수열의 시간 복잡도
피보나치 수열은 아래 점화식으로 정의된다.

n번째 피보나치 수를 구하는 가장 간단한 방법은 아래와 같은 코드를 작성하는 것이다.
def fib(n):
if n==0:
return 0
if n==1:
return 1
else:
return fib(n-1)+fib(n-2)
그리고 1부터 10까지 피보나치를 구한다면 아래와 같이 반복문을 쓰면 된다.
for n in range(10):
print(fib(n))
그런데 한번 fib(20), fib(30), fib(40) 과 같이 점점 수를 증가시켜보자.
fib(40) 을 구하는 정도까지 가면 계산 결과를 구하는데 시간이 꽤 걸리는 것을 알 수 있다.
그 원인을 찾기 위해 한번 피보나치 수열을 구하는 fib 함수가 어떻게 호출되는지 살펴보자.
피보나치 함수의 호출을 재귀 트리 형태로 나타내면 아래와 같은 콜그래프가 그려진다.

이 그래프는 fib(4) 에 대한 콜 그래프이다.
이 트리를 T4 라고 하자.

그리고 이 그래프가 fib(5) 에 대한 콜 그래프이다.
이 트리를 T5 라고 하면 그 왼쪽에 T4가 있음을 알 수 있다.
따라서 Tn 트리를 그리는데는 왼쪽에 Tn-1 이 서브트리로, 오른쪽에 Tn-2 가 서브트리로 들어가는 것을 알 수 있다.
이제 각각의 노드에 대해 fib() 함수를 호출할 것이다.
그러면 fib(4) 는 9번의 fib()함수를 호출한다. 그리고 fib(5) 는 16번의 함수 호출이 필요하다.
이때 T(n) 을 fib(n) 을 실행했을 때 fib() 함수가 호출되는 횟수라고 정의하자.
그러면 Tn 트리를 그리는데 Tn-1, Tn-2 트리가 필요하다는 점에서 아래와 같은 식을 쓸 수 있다.

그리고 아래와 같은 초기값을 가진다.

그런데 이 모양을 보니 마치 피보나치 수열의 정의와 닮은 것을 볼 수 있다.
따라서 T(n) 의 값은 피보나치 수열과 연관성이 있다.
차이가 있다면 피보나치 수열은 Fn = Fn-1 + Fn-2 로 정의 되지만, T(n) = T(n-1) + T(n-2) + 1 로 정의 되기 때문에, 항상 피보나치 수열보다 큰 값을 갖는다.
하지만 그 증가하는 양상은 피보나치 수열과 비슷하게 지수적으로 증가한다.
n번째 피보나치 수열의 값은 아래와 같이 근사되기 때문이다.

따라서 n값이 증가할 때마다, fib(n) 의 실행시간은 지수적으로 증가한다.
(더 구체적으로는 1.6배씩 증가한다.)
만약 fib(45) 를 구하는데 5분의 시간이 걸렸다면, fib(46)을 구할 때는 1.6배 증가한 약 8분의 시간이 걸릴 것이다.
함수의 호출 횟수를 줄이기 위해 아래와 같은 방법으로 코드를 바꿀 수 있다.
def fib2(n):
if n == 0:
return 0
if n == 1:
return 1
else:
a, b = 0, 1
for _ in range(2, n + 1):
a, b = b, a + b
return b
이 방식은 사람이 피보나치 수를 계산하는 것과 같은 방법이다.
피보나치 수를 계산할 때, n-1 번의 덧셈만 하면 된다.
또는 아래와 같은 방법을 사용할 수 있다.
def fib3(n, memo={}):
if n in memo:
return memo[n]
if n == 0:
return 0
if n == 1:
return 1
else:
memo[n] = fib3(n-1, memo) + fib3(n-2, memo)
return memo[n]
이 방법을 memoization 이라고 한다.
한번 구해놓은 결과값을 별도 공간에 저장해두고, 이미 구해서 저장해둔 값을 다시 필요로 하는 경우, 그 값을 꺼내서 바로 돌려주는 방식이다.
이런 기법을 dynamic programming 이라고 한다.
이 기법에 대해서는 뒤에서 더 자세히 정리한다.
'CS > 알고리즘 분석' 카테고리의 다른 글
| [알고리즘분석] 3. 탐욕법 (Greedy) (0) | 2024.04.23 |
|---|---|
| [알고리즘분석] 2. 동적 계획법 (Dynamic Programming) (0) | 2024.04.23 |
| [알고리즘분석] 1. 분할 정복 (Divide and Conquer) (1) | 2024.04.23 |
