허프만 코드와 데이터 압축
컴퓨터는 문자를 그대로 이해하지 못한다.
따라서 문자를 컴퓨터가 이해할 수 있도록 숫자로 바꾸어주어야 한다.
문자를 숫자로 변환하는 것을 '인코딩'
숫자에서 다시 문자로 변환하는 것을 '디코딩' 이라고 한다.
예를 들어 아래와 같은 규칙의 코드 표가 있다면

a,b,c,d 4개 문자로 구성된 아래 문자열을 그 아래처럼 인코딩할 수 있다.


13자리 문자열이 26자리 bit 리스트로 인코딩되었다.
Prefix-Free code
문자열을 인코딩할 때 사용하는 코드 표는 다른 규칙의 코드표를 사용해도 된다.

이런 코드 표를 사용하더라도 문제없이 인코딩과 디코딩이 가능하다.
이때, 각각의 bit 가 선택됨에 따라 어떤 문자를 가리키게 되는지를 이진트리로 나타낼 수 있는데

위와 같이 나타난다.
이 코드표를 사용하여 위에서 언급한 abcd로 구성된 문자열을 인코딩하면
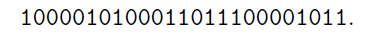
이렇게 인코딩되며, 그 길이는 25 로 전보다 1이 줄어들었음을 알 수 있다.
인코딩된 코드로부터, 다시 문자열로 디코딩하기 위해서는 한가지 규칙이 규칙이 필요하다.
바로 코드 표의 규칙상 어떤 코드도 다른 코드의 prefix가 될 수 없다는 규칙이다.
이 규칙이 깨지면 디코딩을 할 때 서로 다른 2가지 방법의 디코딩 방법이 생길 수 있다.
Huffman Code
허프만 코드는 임의 문자열을 인코딩한 결과가 제일 짧게 나오도록 하는 인코딩 방식을 의미한다.
우선 일반적으로 제일 짧게 인코딩하려면 인코딩하려는 각 문자를 leaf로 하는 extended binary search tree 를 그리면 된다.

그리고 왼쪽을 0, 오른쪽을 1 이라고 정의하면 (정의하기 나름이다.)
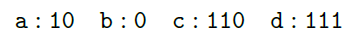
이런 코드가 나온다.
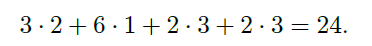
그리고 처음에 본 그 abcd 문자열의 인코딩 결과가 24비트로 더 줄어들었다.
어떤 문자가 주어질지 모르는 상황에서는 위 방식처럼 etended binary search tree 를 그리는 것이 적합하다.
하지만 어떤 문자의 빈도수를 추가로 알고 있다면, 평균적으로 자주 나오는 문자를 더 짧게 인코딩하고, 자주 나오지 않는 문자를 길게 인코딩하여 최적화를 할 수 있을 것이다.
허프만 코드가 이 아이디어를 사용한다.
그 구체적인 아이디어는 다음과 같다.
1. 제일 빈도수가 낮은 코드 2개를 합하여 sibling leaf node 로 둔다. 그리고 그 부모 노드는 그 둘의 빈도수 합이다.
2. 1에서 구한 빈도수 합을 포함한 전체 빈도수 리스트에서 빈도수가 제일 낮은 2개를 골라 묶는다.
역시 그 부모는 빈도수의 합이다.
3. 1, 2 과정을 반복하여 하나의 트리를 만든다. 이 트리를 코드로 나타내면 가장 최적의 인코딩 길이를 갖는 코드가 되며, 이 코드를 허프만 코드라고 부른다.
그 증명은 생략한다.
허프만 코드의 구현 방법과 시간 복잡도
1. 빈도수 순으로 정렬하고, 제일 작은 2개를 합한다. 다시 정렬하고, 제일 작은 2개를 합한다. 최악의 경우 n번의 정렬을 수행하므로 O(n²logn) 시간복잡도를 갖는다.
2. 굳이 정렬할 필요없이 전체 순회를 하면서 제일 작은 2개를 찾는다. 한번 2개를 찾는데 O(n) 시간이 걸리므로 전체 시간복잡도는 O(n²) 이다.
3. 우선순위 큐를 활용하여 전체 데이터를 다 넣은 뒤 (또는 O(n) 시간으로 힙으로 만든 뒤) 2번 pop 하고 한번 push 하는 과정을 n번 반복한다. pop, push 에 O(log n) 이 소모되므로, 전체 시간복잡도는 O(n log n) 이다.
만약 이미 정렬되어있는 경우, 2개의 큐를 사용하여 O(n) 시간에 구할수도 있다.
첫번째 큐에는 빈도수 순으로 정렬된 데이터를 넣고, 두번째 큐는 비워둔다.
1. 첫번째 큐에서 제일 작은 2개 데이터를 뺀다. (즉 pop 2번)
2. 이를 더해서 두번째 큐에 넣는다.
3. 첫번째 큐에서 값을 하나 뺀다. 두번째 값을 빼기 전 두번째 큐의 front 에 있는 값과 비교하여 더 작은 값을 취해 더한 뒤 두번째 큐에 넣는다.
4. 이 과정을 반복한다.
'CS > 알고리즘 분석' 카테고리의 다른 글
| [알고리즘분석] 2. 동적 계획법 (Dynamic Programming) (0) | 2024.04.23 |
|---|---|
| [알고리즘분석] 1. 분할 정복 (Divide and Conquer) (1) | 2024.04.23 |
| [알고리즘분석] 0. Preliminaries : 덧셈/곱셈 & 피보나치 수열의 시간복잡도 (0) | 2024.04.22 |
