분할 정복은 말 그대로 주어진 문제를 분할하고, 분할한 조각을 정복(해결) 하는 방식으로 해결한다.
그리고 이 과정은 재귀적으로 발생한다.
지난 글에서 정리한 피보나치 수열도 그 값을 구할 때 '재귀'를 주요 아이디어로 활용하였듯, 분할 정복도 다른 관점에서 재귀를 활용하는 알고리즘이다.
이제부터 다양한 분할 정복 알고리즘과 그들의 시간복잡도를 구해본다.
카라츠바 곱셈 계산 (Karatsuba Method)
일반적인 곱셈 계산
곱셈은 덧셈의 반복이므로, 먼저 덧셈을 하는 과정을 생각해보자.
1234와 5678을 더한다면 일반적으로 아래와 같은 과정으로 진행된다.

두 피연산자는 정렬되어있어 i번째 자릿수는 같은 열에 위치한다.
각 자리수를 더해 만약 올림(carry)이 발생한다면, 다음 자리수에 넘겨 함께 더한다.
4자리수의 덧셈을 할 때는 위에서 자릿수 덧셈 4번과 올림 덧셈 2번, 총 6번의 덧셈을 했다.
(덧셈은 한번에 2개의 수를 더하는 것으로 생각한다.)
만약 6자리 수라면 자릿수 덧셈 6번과 올림 덧셈 최대 5번 (1의 자리를 제외한 모든 자리에서 올림수 덧셈) 이 발생할 수 있다.
이를 일반화하면 n자리수 덧셈을 할 때는 최대 n번의 자릿수 덧셈과 n-1 번의 올림 덧셈, 총 2n-1 의 덧셈을 할 수 있다.
이로부터 덧셈의 시간복잡도는 O(n) 이라는 결론도 얻을 수 있다.
이제 곱셈을 생각해보자.
만약 1234 와 5678을 곱한다면, 아래와 같이 곱셈한다.
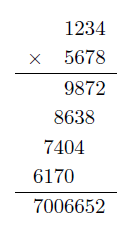
곱셈은 한자리 수 곱셈과 한 자리수 덧셈의 반복으로 이루어진다.
처음에는 1234 와 8의 곱셈
다음에는 1234와 7의 곱셈...
이를 반복하는 과정이다.
이를 일반화하여 생각해보자.
n자리 수와 어떤 한자리 수를 곱한 결과는 최대 몇자리가 나올 수 있을까?
n자리 수에 10을 곱했을 때 n+1 자리가 되기 때문에, 어떤 한자리 수를 곱한 결과는 최대 n+1 자리가 될 수 있다.
이를 그림으로 그리면 아래와 같다.

따라서 곱셈을 구하는 데에는 (n번의 곱셈과, 최대 n-1 번의 덧셈)을 필요로 하는 1자리수 곱셈을 n 번 반복 한뒤,
마지막에는 n개의 shift 된 n+1자리 수를 모두를 더하는 연산까지 (2n-1) * (n-1) 번 진행하므로 (2개 수를 더할 때 2n-1 덧셈을 1번 하므로, n개 수를 더할 땐 n-1 번의 덧셈을 한다.)
필요한 총 연산의 횟수는 (2n-1) * n + (2n-1) * (n-1) = (2n-1) ^ 2
따라서 곱셈의 시간복잡도는 O(n²) 이다.
그런데 놀랍게도 이보다 더 빠른 시간안에 곱셈을 연산할 수 있는 방법이 존재한다.
카라츠바 방법
카라츠바의 방법은 n자리수 U와 V를 곱할 때, 이 두 수를 상위 n/2 자리, 하위 n/2 자리수로 나누어서 곱셈을 하는 아이디어를 사용한다.
즉, 위의 1234와 5678의 곱을 예시로 들면
1234 = 12 * 10^2 + 34
5678 = 56 * 10^2 + 78
로 쪼개고, 이렇게 쪼갠 상태에서 곱셈을 한다.
이를 수학적으로 일반화하여 표현하면 아래와 같다.
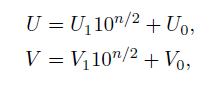
(이때 n/2 는 ceiling 으로 받아들이자. n = 3 이면 n/2 = 2 가 된다.)
이렇게 쪼갠 결과물을 곱하면

다음과 같은 식이 나온다.
이를 통해 알 수 있는 것은 n자리수 U, V 의 곱을 n/2 자리수 U1, U0, V1, V0 간의 곱으로 표현할 수 있다는 것이다.
게다가 이 식에서

다음과 같이 이 식을 변환할 수 있다.
이미 U1V1 과 U0V0이 필요해서 구해둔 상황에, 이를 그대로 재활용이 가능하도록 식을 재구성했다.
따라서 이 식을 계산하는데 필요한 연산은
U1V1, U0V0, (U0 + U1)(V0 + V1) 3가지 이며, 각 연산의 피연산자는 모두 n/2 자리수이다.
따라서 n자리 수의 곱셈을 n/2 자리수 곱셈 3개로 수행할 수 있게 되었다.
이를 1234 * 5678 에 적용해보면 아래와 같다.

이 과정을 코드로 짜면 아래와 같이 짤 수 있다.
mult(u,v)
{
// u,v: n digits
if both u and v are one-digit numbers
return u*v; // one-digit (or machine) multiplication
else
u1,v1 <- fisrt n/2 digits of u and v
u0,v0 <- remaining n/2 digits of u and v
uv0 <- mult(u0,v0) // recursive call
uv1 <- mult(u1,v1)
w <- mult(u0+u1, v0+v1) - uv0 - uv1 // ’+’: n/2-digits addition
return [uv1*10^n + w*10^(n/2) + uv0] // done by shifting + adding
}
n자리수를 n/2 자리수의 곱셈들로 치환하는데, 다시 n/2 자리수의 곱셈은 n/4자리수의 곱셈으로 치환할 수 있다.
반씩 계속 줄이다가 1자리수가 되면 구구단에서 하는 곱셈을 하면 된다.
이제 이 알고리즘의 시간복잡도를 분석해보자.
위에서 작성한 mult() 함수의 실행 시간을 T(n) 이라고 하자.
n 은 현재 곱하려는 수의 자리수이다.
만약 자리수가 1자리수가 되면 ( T(1) 이면 ) 1자리 곱셈을 하고 바로 반환하므로 T(1) = 1 이다.
1이 아닌 n자리수를 곱하는 상황이라면
1. u, v 를 n/2 자리로 분할하고
2. 3개의 n/2 자리수 곱셈을 구하기 위해 mult() 함수가 3번 호출된다.
3. 그리고 더한 결과물을 하나로 합치는데 n에 비례하는 시간이 든다.
( return 코드를 보면, 10^n 을 하는 시점에서 n번 곱하는 연산이 들어간다. )
따라서, T(n)을 아래와 같이 쓸 수 있다.

T(n) 을 실행하는 시간은, T(n/2)을 3번 호출하고, 3번의 return 에서 n에 비례한 연산, 1번의 n/2 자리 분할 등의 연산에 n에 비례한 Cn의 시간이 들어간다고 할 수 있다.
C값을 어떻게 잡을지 모르지만, 확실히 n에 비례한 시간이고, C값에 따라 T(n)이 3 T(n/2) + Cn 보다 작거나 같은 것은 확실하다. 구체적인 n의 계수를 구하지 않아도 되는 이유는, 상수 C라는 계수값이 자릿수 n에 상관없이 일정해서 n에 따른 시간복잡도 변화에 영향을 크게 주지 않기 때문이다.
이제 이 부등식을 아래와 같이 재귀적으로 확장할 수 있다.
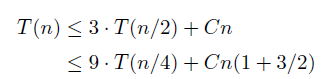
이 과정은 T(1)이 될 때까지 반복된다.
T(1)이 되기까지 n 이 매번 2로 나눠지는 과정을 반복하므로, 반복하는 횟수 k를 아래와 같이 계산할 수 있다.
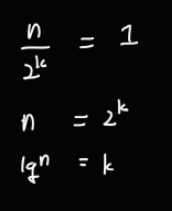
따라서 이 반복은 lgN번 반복한다. (지난 글에서 정한 notation 대로 밑이 2인 로그이다.)
위 수식 아래와 같이 지수를 이용하여 표현하면
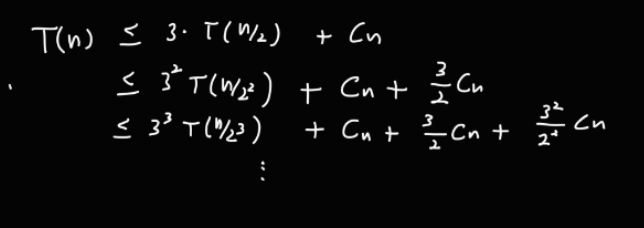
이렇게 되고, 이를 방금 구한 반복 횟수를 이용해서 표현하면
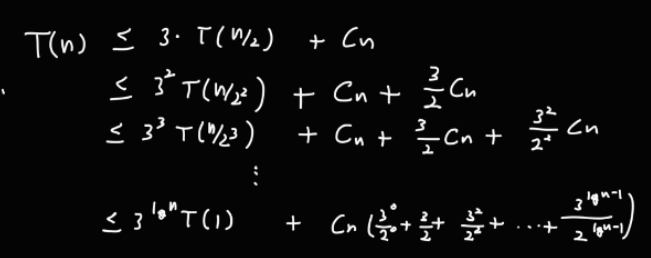
이때, Cn 에 붙은 수식이 등비급수의 합 공식을 이용하여 아래와 같이 표현할 수 있다.

이 값을 구하는 시간복잡도는 아래와 같이 구할 수 있다.

3의 lgN 승은 n의 lg3 승과 같다.
이때 T(1) 앞에 곱해진 값은 3의 lgN 승 = n의 lg3 승이므로

이렇게 구할 수 있다.

따라서 최종적으로 구한 시간복잡도는 O(n의 lg3승) 이다.
이 lg3 < lg4 = 2 이므로, 기존 시간복잡도보다 개선된 시간에 n자리수 곱셈을 수행할 수 있다.
T(n)의 전개 과정을 아래와 같이 트리로 표현할 수도 있다.

카라츠바 방법은 1960년대에 나온 방법이다.
지금은 이 방법을 더 일반화한 방법까지 논의되었다.
카라츠바는 n자리 수를 2개 파트로 쪼개서 연산하는 방법을 사용했다.
만약 쪼개는 파트가 2개가 아니라 3개, 4개, ..., k개 라면 어떨까?
기존 알고리즘대로라면 각각의 k자리 파트에 대한 곱셈 연산은 k² 번의 곱셈이 필요하다.
하지만 카라츠바와 비슷한 방법을 적용하면, 2k-1 번의 곱셈으로 k자리 수를 계산하고 O(n) 시간에 전체 조각을 합칠 수 있다.
따라서 이를 아래와 같이 나타낼 수 있다.


이 식에 k = 2 를 대입하면 위에서 구한 시간복잡도가 똑같이 나오는 것을 볼 수 있다.
만약 k값을 충분히 크게 한다면, 이론적으로 정수 곱셈의 시간복잡도는 O(n^(1+ε)) 가 된다.
ε는 충분히 작은 임의 양의 수이다.
행렬 곱셈
n x n 행렬을 곱셈하는데는 일반적으로 알려진 방법을 사용할 경우 O(n³) 의 시간복잡도를 갖는다.
곱셈 결과 특정 위치의 값을 계산하는데, n번의 곱셈을 해야하고, 이를 n² 번 반복해야 하기 때문이다.
New Breakthrough Brings Matrix Multiplication Closer to Ideal | Quanta Magazine
By eliminating a hidden inefficiency, computer scientists have come up with a new way to multiply large matrices that’s faster than ever.
www.quantamagazine.org
그런데 이 기사에 따르면, 행렬 곱셈의 시간복잡도가 점점 n² 에 가깝게 줄어들고 있다고 한다.
가장 먼저 시간복잡도를 줄인 방법은 O(n^(lg 7)) 으로 줄인 방법이었다.
기존보다 곱셈 연산 횟수를 줄이고, 미리 곱셈해둔 값을 조합한 연산으로 모든 위치의 값을 계산하는 것으로
이런 점에선 카라츠바의 아이디어와 유사하다고도 볼 수 있다.
그렇다면 행렬 곱셈의 시간복잡도는 O( n² ) 보다 더 줄어들 수 있을까?
절대 그렇지 않다.
행렬 곱셈을 하려면 행렬의 모든 원소를 최소 한번씩은 읽어야 하기 때문에 n² 의 순회가 반드시 필요하기 때문이다.
그렇다면 지금까지 논의한 카라츠바 곱셈과 행렬 곱셈의 최적화는 모든 상황에서 항상 빠르다고 할 수 있을까?
시간복잡도 상으로 학교에서 사용하는 방법보다 빠른 것은 맞지만, 실제 계산할 때 적당히 큰 수에 대해서는 학교에서 사용하는 방법이 더 빠르다.
그 이유는 최적화를 하기 위해 거치는 부수적인 작업들이 작은 수를 계산할 때는 오히려 더 복잡해서 연산량을 줄이는 이점보다 더 큰 손실을 가져오기 때문이다.
이분 탐색의 시간 복잡도
정렬된 배열 K 에 대해 아래와 같이 이분탐색 알고리즘을 구현하였다.
binsearch(K,l,u,x)
{ // the size of list n=u-l+1
if (l>u) // n=0
return -1
m=floor((l+u)/2)
if K[m]=x
return m
else if K[m] < x
return binsearch(K,m+1,u,x)
else
return binsearch(K,l,m-1,x)
}
이 함수의 최악의 실행 시간을 T(n) 이라고 하자. (즉, 수를 찾기 위해 가장 깊이 들어간 경우이다.)
그러면 아래와 같이 상수 C를 이용하여 표현할 수 있다.

T(1) 과 T(0) 에서 함수의 실행이 종료되므로, 이를 전개하면 카라츠바에서와 마찬가지로 lg n 번 ( T(0) 의 경우 lg n + 1번 )의 함수 호출이 발생한다.
따라서 이를 전개하면

병합 정렬의 시간 복잡도
병합 정렬은 분할 정복 알고리즘의 일부로서, 아래와 같이 재귀로 구현한다.
mergesort(A(l..r))
{
if (l<r)
m=(l+r)/2
mergesort(A(l..m))
mergesort(A((m+1)..r))
merge(A(l..m),A((m+1)..r))
}
mergesort() 함수는 n 개의 데이터가 들어있는 배열을 정렬하고,
위 함수에서 merge 는 n/2 개의 정렬된 데이터가 들어있는 두 배열을 합쳐 새로운 정렬된 배열을 만드는 함수이다.
merge 는 n/2 개의 정렬된 데이터가 들어있는 두 배열 모두 읽어야 하므로, n 의 시간이 걸린다.
따라서 merge 는 n에 비례한 시간이 걸리게 된다.
이를 함수로 구현하면 아래와 간다.
merge(A(l..m..r))
{
copy A(l..r) into B(l..r)
i <- l
j <- m+1
k <- l // index for recollecting into A
while (i<=m and j<=r)
if (B(i)<=B(j))
A(k++) <- B(i++)
else
A(k++) <- B(j++)
if (i>m) // taking care of the remaining part
while (j<=r)
A(k++) <- B(j++)
else
while (i<=m)
A(k++) <- B(i++)
}
만약 merge 하는 데이터의 크기가 다르다면, 최소 min(n, m) 번의 비교가 발생하고, 최대 m + n - 1 번의 비교가 발생한다.
데이터를 옮기는 데는 항상 m + n 번의 횟수가 필요하므로, 서로 다른 데이터 m, n 에 대해서는 O( m + n ) 의 시간복잡도를 갖는다.
이제 n개의 데이터를 정렬하는 병합 정렬 알고리즘의 시간복잡도를 구해보자.
정확히는 위의 mergesort() 함수의 실행시간의 최악을 구한다.
n / 2 를 정렬하는 함수가 2번 호출 되고, 이를 병합하는데 n 에 비례한 시간이 걸리므로

이렇게 작성할 수 있다.
이제 이를 전개하면

따라서 시간복잡도는 O(n lg n) 이다.

이를 그래프로 그리면 아래와 같은 extended binary tree 가 나오기 때문에, 함수의 호출횟수는 2N - 1 과 같아진다.
퀵 소트의 시간 복잡도
퀵소트는 아래와 같이 구현할 수 있다.
quicksort(A(l..r))
{
if(l<r)
p <- partition(A(l..r)) // ==> A(l..p-1) [p] A(p+1..r)
quicksort(A(l..p-1))
quicksort(A(p+1..r))
}
퀵소트의 핵심은 partiion() 함수이다.
이 함수가 pivot 을 구하고, 이를 기준으로 배열을 쪼개서 정렬하게 된다.
피벗을 구하는 방식은 배열의 첫번째 원소를 일단 피벗으로 잡은 뒤, 나머지 원소를 피벗과 비교하여 작은 값은 피벗 앞에, 큰 값은 피벗 뒤에 두는 식으로 배열을 조정하는 것으로 in order 정렬한다.
따라서 모든 값을 피벗과 한번씩 비교하게 되므로 partition 함수의 실행시간은 O(n) 이다.
하지만 이 함수의 실행결과, 피벗의 위치가 항상 중간이 아닐 수 있다.
만약 이미 정렬된 배열에 대해 퀵소트를 수행한다면
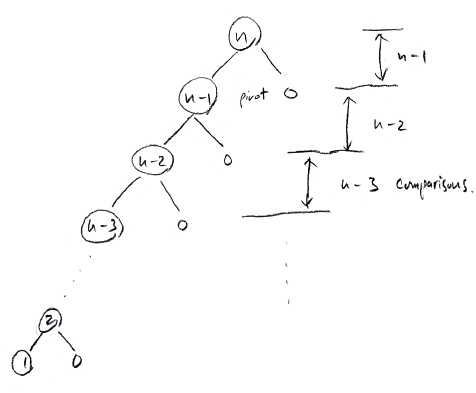
아래와 같은 과정으로 정렬이 진행되어 깊이 n의 트리를 그리게 된다.
따라서 O(n²) 의 시간이 걸릴 수도 있다.
따라서 퀵 소트의 일반적인 실행시간을 구하는 것은 꽤 까다로운 일이다.
하지만 퀵 소트의 평균 실행시간은 O( n log n ) 이라는 것이 잘 알려져있다.
이제 왜 그렇게 계산이 되는지 따라가보자.
먼저 퀵 소트의 파티션이 만드는 피벗이 매번 주어진 배열의 2/3 위치에 존재하게 된다고 가정하자.
그러면 아래와 같이 T(n) 을 작성할 수 있다.
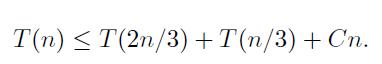
이때, T(1) 이 되면 종료되므로, 트리의 높이를 구해보면

다음과 같다.
n/3 에 대해서 구하지 않은 이유는, n/3 이 더 빠르게 감소하기 때문에 트리의 높이가 더 낮게 나오기 때문이다.
그림으로는 아래와 같다.
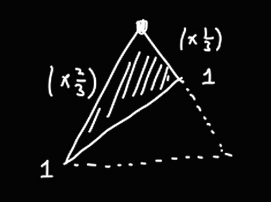
따라서 Cn 이 (log n / log3 - 1) 번 반복되므로, 시간복잡도는 O(n log n) 이다.
이를 일반화하여 피벗이 배열을 0 < α < 1 인 α 로 분할한다고 하자.
그러면 아래와 같이 T(n)을 쓸 수 있다.
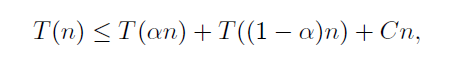
만약 α가 1 - α 보다 큰 수라면 이 α에 의해 트리의 높이가 이렇게 결정된다.

따라서 Cn 이 lg n / lg(1/α) 번 반복되므로, 시간복잡도는 O(n log n) 이다.
이제 마지막으로 random 한 n 개의 입력이 주어졌을 때 이를 k, n-k-1 개로 분할 하는 경우를 생각해보자. (1을 더 빼는 이유는 파티션은 정렬 기준에서 빠지기 때문이다.)
n 개 입력이 random 하게 주어지므로, 모든 n개 수의 선택 확률은 동일하다.
따라서 0, n-1 과 같은 극단적인 경우가 선택될 확률은 낮기 때문에 recursion tree 의 높이는 log N 이 된다.
따라서 퀵소트의 평균 실행시간은 O ( n log n ) 이다.
k 번째로 큰 수 선택하기 (Selection Problem)
n 개의 서로 다른 수가 무작위 순으로 주어질 때, 이들을 정렬 했을 때 k 번째에 위치한 수를 kth order statistic 이라고 한다.
가장 작은 수를 찾는 것은 쉽다.
그냥 n 개의 수를 모두 돌면서 지금까지 돌면서 저장해둔 제일 작은 수보다 더 작다면 그 수를 저장하는 방법으로 O(n) 시간에 찾을 수 있다.
최댓값도 비슷한 방법으로 O(n) 시간에 찾을 수 있다.
2번째로 작은수, 2번째로 큰 수도 2개의 수를 저장하면서 탐색하면 O(n) 시간에 찾을 수 있다.
하지만 정렬했을 때 중간에 있는 수를 찾는 문제로 이 문제를 바꾸면 얘기가 달라진다.
중간이 아니더라도 상위 10%에 있는 수를 찾는 식으로 비율로 접근하면 정렬 없이 찾는 것이 쉽지 않다.
따라서 O(n log n) 의 시간이 적어도 걸린다고 생각할 수 있다.
하지만 이 문제를 선형 시간에 푸는 알고리즘이 존재한다!
Quick Select
먼저 quick select 알고리즘을 살펴보자.
QuickSelect(A[1..n],k)
1. Partition A[1..n] (using, for example, A[1] as a pivot)
==> A [1..j-1] [j] [j+1..n] // after partition, we know pivot’s rank, say, j.
2. If j=k,
return A[j] (pivot)
else if k<j,
RSelect(A[1..j-1],k)
else // k>j
RSelect(A[j+1..n],k-j)
이 알고리즘은 quick sort 랑 유사하게 파티션을 사용해서 피벗을 찾고, 찾은 피벗이 찾으려는 k번째 수 인지 확인하는 방법으로 원하는 수를 찾는다.
상위 10% 와 같은 비율로 접근하더라도, 입력에 들어오는 배열의 크기를 안다면 이 비율을 계산해서 k 값을 결정한 뒤, 그 수를 찾으면 된다.
퀵소트와 마찬가지로 최악의 경우, O(n²) 의 시간복잡도를 갖는다.
하지만 평균적으로는 O(n) 의 시간복잡도를 갖는다.
퀵소트 때와 마찬가지로 α 비율로 파티션이 수를 나눈다고 하면
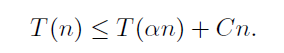
주어진 함수의 실행 시간을 위와 같이 표현할 수 있다.

위 식을 전개하면 위와 같은 과정으로 O(n)이 되는 것을 알 수 있다.
평균적으로 recursion tree 의 높이가 n 이 되는 경우는 드물기 때문에 평균 시간은 O(n) 이라고 하는 것이 합리적이다.
(물론 이 설명이 엄밀한 논증은 아니긴하다.)
RSelect
Quick Select 는 피벗을 처음 고를 때, 배열의 맨 앞의 값과 같이 임의 값을 지정해서 고른다.
이 경우, 입력값의 형태에 따라 선택 알고리즘의 시간복잡도가 영향을 받게 된다.
따라서 R Select 는 이 문제에 대처하고자 피벗값을 임의로 고르자는 아이디어를 추가했다.
RSelect(A[1..n],k)
1. Choose a random pivot from A[1..n].
2. Partition using the pivot.
==> A [1..j-1] [j] [j+1..n] // after partition, we know pivot’s rank, say, j.
3. If j=k,
return A[j] (pivot)
else if k<j,
RSelect(A[1..j-1],k)
else // k>j
RSelect(A[j+1..n],k-j)
따라서 시간 복잡도로만 보면 quick select 와 동일한 시간복잡도를 갖는다.
DSelect
지금까지 본 Select 알고리즘은 최악의 경우에 O(n²) 의 시간복잡도를 가졌다.
그러나 DSelect는 항상 O(n) 의 시간복잡도를 갖는다.
DSelect 의 아이디어도 피벗 선택과 관련이 되어있다. 기존 RSelect 에서 사용한 것처럼 랜덤하게 피벗을 잡지말고, 조금 더 합리적인 방법으로 피벗을 고르는 것이 DSelect 의 아이디어이다.
DSelect 에서는 mom (median of median) 을 피벗으로 고른다.
이 방식으로 피벗을 고르면, 언제나 재귀 트리가 직선으로 그려지는 피벗 선택방식보다 나은 피벗 선택방식을 고르는 것을 보장할 수 있다.
DSelect(A[1..n],k)
1. Find medians of subarrays A[5m+1..5m+5] of size 5, m=0,...,n/5;
put them into array M[0..n/5].
2. mom = DSelect(M[0..n/5], n/10) // recursive call; median of median
3. Partition A[1..n] using mom as a pivot.
==> A [1..j-1] [j] [j+1..n] // pivot’s rank is j.
4. If j=k,
return A[j] (pivot)
else if k<j,
DSelect(A[1..j-1],k)
else // k>j
DSelect(A[j+1..n],k-j)
DSelect의 알고리즘은 위와 같다.
먼저 주어진 배열을 일렬로 나열한 뒤, 5개씩 끊어서 그 5개로 구성된 subarray의 median 값을 골라 M[] 배열에 넣는다.
그러면 n/5 개의 원소로 구성된 M 배열이 만들어진다.
그러면 다시 그 M 배열에서 median값을 찾아 새로운 M배열에 추가하는 과정을 반복한다.
최종적으로 하나의 값이 남으면 이를 pivot으로 삼아서 정렬을 진행한다.
이 방법을 사용하면, mom 값이 전체에서 항상 상위 30%~70% 이내에 위치함을 보장할 수 있다.

5개씩 끊은 서브 배열을 정렬해서 위와 같이 아래에서 위로 나열할 때, 3번째 값이 median 값이다.
다른 값에 대해서도 같은 방식으로 정렬하면 위와 같은 형태가 된다.

이를 반복해서 쭉 나열하면 위와 같이 그림이 그려지고,
mom 값은 왼쪽 아래 위치한 값들보단 크고, 오른쪽 위에 있는 값들보단 작다는 것이 보장된다.
그리고 일반적으로 왼쪽 아래와 오른쪽 위에 위치한 값들은 전체의 약 30%를 차지한다.
따라서 mom 값은 전체에 30% ~ 70% 범위 안에 있음을 보장할 수 있다.
따라서 pivot 으로 구한 mom 값을 j 라고 하면

이렇게 나타낼 수 있다.
그리고 이로부터 DSelect 함수의 실행시간을 아래와 같이 나타낼 수 있다.

T(n/5) 는 mom 값을 구하는 과정의 시간
T(7n/10) 은 4에서 하위30 또는 상위 30를 제거한 나머지 70% 값에 대해 재귀적으로 값을 찾는 경우를 말한다.
cn 은 구한 피벗 기준으로 값들을 앞, 뒤로 옮기는 과정에서 소요되는 시간이다.
그런데 n/5 + 7n/10 = 9n / 10 < n 이라서 이 함수의 실행시간은 O(n) 이 된다.
(quick select 의 시간복잡도를 계산했던 과정을 따라가면 된다.)
그리고 이때 median 으로 분류할 sub array 의 크기를 5가 아닌 7로 잡아도 되는데, 5가 제일 최적이 되는 수가 된다.
7로 하는경우, T(n/7) + T(5n/7) 이 되며, 이 시간은 5로 했을 때 보다 조금 더 긴 시간이 걸린다.
심지어 3을 골랐을 경우에는 T(n/3) + T(2n/3) + cn 이 되어, 시간복잡도가 O(n log n) 이 된다!
(퀵 소트에서 했던 시간복잡도 계산이 그대로 들어간다.)
'CS > 알고리즘 분석' 카테고리의 다른 글
| [알고리즘분석] 3. 탐욕법 (Greedy) (0) | 2024.04.23 |
|---|---|
| [알고리즘분석] 2. 동적 계획법 (Dynamic Programming) (0) | 2024.04.23 |
| [알고리즘분석] 0. Preliminaries : 덧셈/곱셈 & 피보나치 수열의 시간복잡도 (0) | 2024.04.22 |
