동적 계획법은 어떤 값을 구할 때 반복적으로 이미 구했던 값을 사용하는 경우, 이 값을 미리 기록해두었다가 활용하는 방법의 알고리즘이다.
동적 계획법은 대체로 재귀 형태의 점화식을 가지는 문제를 해결하는데 유용하게 사용할 수 있다.
이항 계수
이항계수는 nCk 조합의 경우의 수를 구하는데 사용된다.
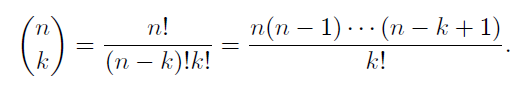
이항 계수의 값은 위와 같이 계산한다.
이때 이항 계수 nCk 를 각각의 값에 따라 쭉 표를 그리듯 그리면 아래와 같이 그려진다.

이 삼각형을 가리켜 '파스칼 삼각형' 이라고 한다.
파스칼의 삼각형에 따르면 이항 계수는 아래와 같은 성질을 지닌다.
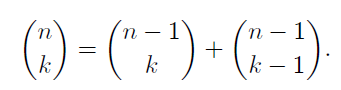
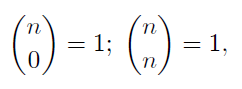
이항계수의 값이 다른 이항계수의 값을 이용해 재귀적으로 표현됨을 알 수 있다.
이 공식을 그대로 함수로 옮기면
def binom(n,k):
if n<0 or k<0: return 0
if n<k: return 0
if k==0: return 1
if k==n: return 1
return binom(n-1,k)+binom(n-1,k-1)
위와 같이 표현할 수 있다.
하지만 피보나치 수열에서 봤던 것처럼 이를 그대로 사용하는 것은 많은 시간이 걸린다.
binom(30, 15) 정도만 되어도 계산에 많은 시간이 걸린다.
이때 bimon(n, k) 의 실행시간을 T(n, k) 라고하면,
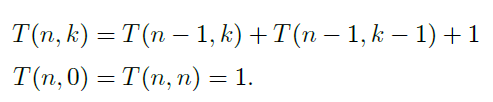
와 같이 정의할 수 있으며,
이를 이용하면 T(n, k) 의 값이 2 x (nCk) - 1 과 같음을 보일 수 있다.

수학적 귀납법으로 위와 같이 증명할 수 있다.
그렇다면 저렇게 생으로 binon() 을 구하는 시간은 n, k 가 커짐에 따라 매우 큰 폭으로 증가하는 것을 알 수 있다.
이를 동적 게획법을 사용해 최적화 해보자.
bottom - up
def binom2(n,k):
memo = {}
if n<0 or k<0: return 0
if n<k: return 0
# boundaries first
for i in range(0,n+1):
memo[i,i]=1
memo[i,0]=1
# interior
for i in range(2,n+1):
for j in range(1,i):
memo[i,j]=memo[i-1,j]+memo[i-1,j-1]
return memo[n,k]
미리 k = 0, k = n 인 상황의 디폴트 값을 정해두고, 삼각형 영역에 있는 모든 이항 계수를 구한다.
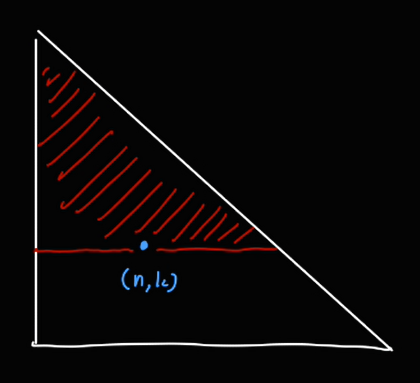
사실 (n, k) 값을 구할 때 필요한 영역은 더 좁다.
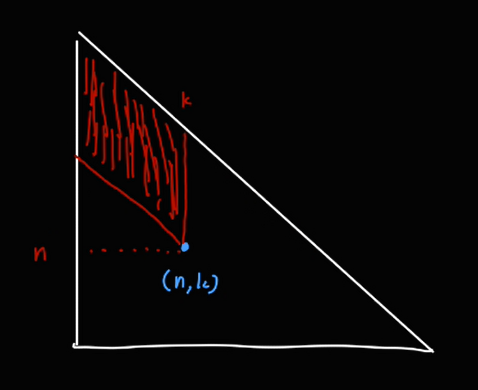
이 영역만 구하면 된다.
따라서 아래와 같이 반복문을 더 개선할 수도 있다.
# interior
for i in range(2,n+1):
for j in range(max(1,i-n+k), min(i,k+1)):
memo[i,j]=memo[i-1,j]+memo[i-1,j-1]
저 영역이 나오는 이유는
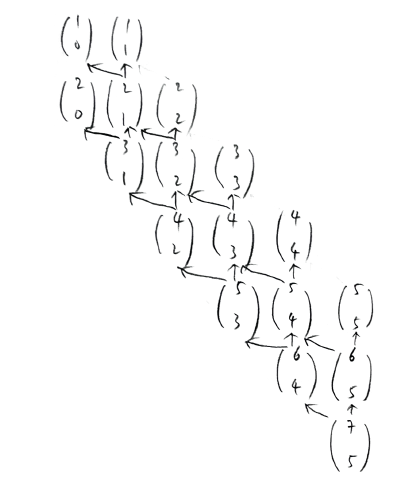
이 그림을 참고하자.
7C5 를 구하는데 필요한 이항 계수의 집합이 위와 같다.
top - down
def memoize(f):
memo = {}
def helper(x,y):
if (x,y) not in memo:
memo[x,y] = f(x,y)
return memo[x,y]
return helper
def binom3(n,k)
if n<0 or k<0: return 0
if n<k: return 0
if k==0: return 1
if k==n: return 1
return binom3(n-1,k)+binom3(n-1,k-1)
binom3=memoize(binom3)
클로저를 이용하여 위와 같이 메모이제이션을 구현할 수 있다.
행렬 곱셈 순서
d1 x d2 크기의 행렬 A, d2 x d3 크기의 행렬 B, d3 x d4 크기의 행렬 C 가 있다고 하자.
행렬 A, B 를 곱하면 그 결과 d1 x d3 크기의 행렬이 나오며, 이때 필요한 곱셈의 연산 횟수는 d1 x d2 x d3 이다.
덧셈은 d1 x d3 x (d2 - 1) 번의 덧셈이 필요하다.
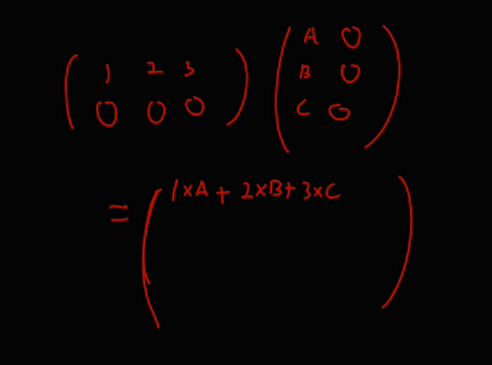
최종 결과로 나오는 d1 x d3 행렬의 원소를 하나 결정하는데, d2번의 곱셈과 d2 - 1번의 덧셈이 필요하다.
이 행렬들의 곱 A B C 를 구할 때, 계산하는 순서는 크게 2가지가 있다.
(A B) C 순으로 할 수도 있고, A (B C) 순으로 할 수도 있다.
이때 (A B) C 순으로 하는 경우, 곱셈의 연산량만 생각한다면
A B 를 구하는데 d1 x d2 x d3 번의 연산을 하고, 그 결과 d1 x d3 크기의 행렬이 나온다.
(AB) C 를 구하는데, d1 x d3 x d4 번의 연산을 하고, 최종 d1 x d4 크기의 행렬이 나온다.
따라서 총 연산량은 d1 x d2 x d3 + d1 x d3 x d4 이다.
만약 A(BC) 순으로 하는 경우
(BC) 를 구하는데 d2 x d3 x d4 번의 연산 이후, d2 x d4 행렬이 나온다.
A(BC) 를 구하는데 d1 x d2x d4 번의 연산 이후 d1 x d4 행렬이 나온다.
따라서 총 연산량은 d2 x d3 x d4 + d1 x d2x d4 이다.
즉, 곱셈 순서에 따라 필요한 연산량이 서로 다르게 나올 수 있다.
만약 A1 ~ An 까지 행렬 n개를 곱하는 상황이 주어졌을 때, 이때 필요한 최소 연산량과 최대 연산량을 한번 구해보자.
(본래는 최소 연산량을 구하는 것이 목적이지만, 최대 연산량 역시 DP를 이용하여 구할 수 있다. 기출 문제)
우선 제일 나이브한 방법은 모든 방법의 곱셈을 다 해보고 그 가운데 원하는 최적값을 찾는 것이다.
헹렬의 곱셈순서는 extended 이진트리를 이용해 아래와 같이 나타낼 수 있다.
만약 A1 ~ A4 까지 곱한다면
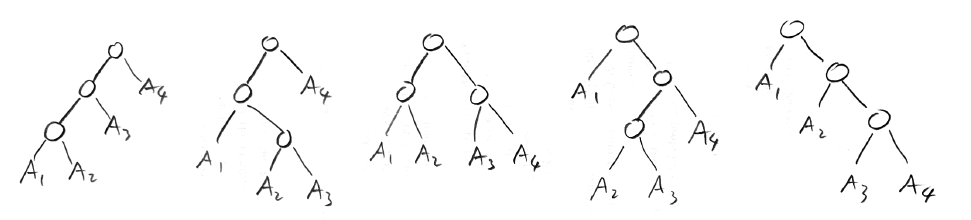
위와 같이 5가지 경우의 수가 있다.
따라서 n개 행렬 곱셈 순서의 경우의 수는 아래와 같이 n-1 개 노드로 이진트리를 만드는 경우의 수, 즉 n-1번째 카탈란 수와 같다.
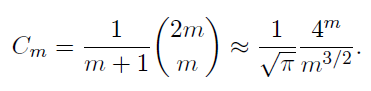
하지만 이 카탈란 경우의 수만큼 모든 행렬 곱셈을 다 해보는 것은 효율적이지 않다.
이를 효율적으로 계산하기 위해 아래와 같이 점화식을 정의해보자.
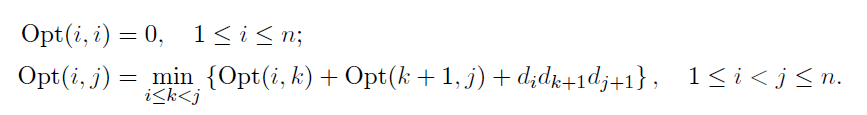
Opt(i, j) 를 i번째 행렬부터 j번째 행렬까지 곱한 최적의 (최소의) 연산량이라고 할 때, 그 값은 위와 같이 구할 수 있다.
i, j 까지 행렬을 곱한 최적의 연산량은 결국 최종적으로 2개의 행렬이 남아 그 둘을 곱해야 하므로
최종적으로 남는 2개 행렬을 연산하고 이 둘을 곱하는 경우의 수를 모두 구해서 그 최소값을 찾으면 된다.
만약 최댓값을 찾는다면 위 공식에서 min 대신 max 만 쓰면 된다.
base case로서 opt(i, i) 인 경우, 같은 행렬은 연산하지 않으므로 연산량은 0이다.
예를 들어
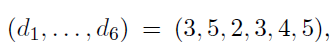
이렇게 연속된 5개 행렬의 차원 정보가 주어졌을 때, 최적의 연산량을 구한다.
opt(i, j) 를 메모이제이션 기법으로 기록하면서 연산할 텐데, 이에 대해 i, j 를 각 축으로 하는 표를 채우면

이렇게 표가 그려진다.
그리고, (i, j) 에 대해 어떤 k 값이 최적이었는지를 표로 출력하면

이렇게 나온다.
이때
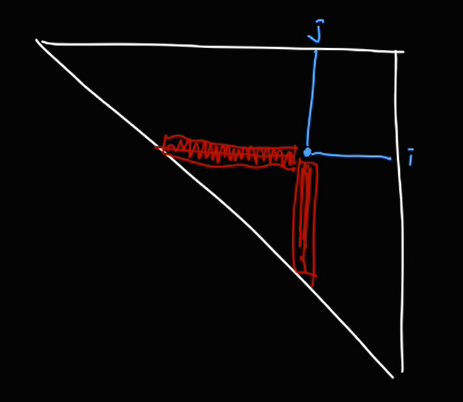
(i, j) 의 값을 구하기 위해서는 빨간색 영역의 값들이 필요하다.
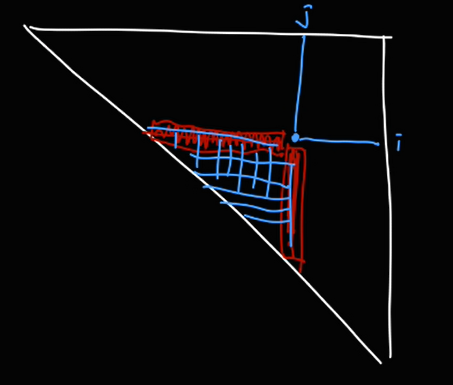
이때 빨간색 영역의 값들에 대해서도 각각의 필요한 값들을 구하다보면 이렇게 삼각형의 영역을 구하게 된다.
만약 이를 바텀업으로 구현한다면
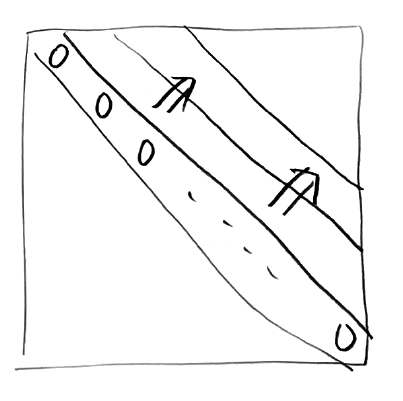
이렇게 대각선 값들을 먼저 구해두고 (초기값 (i, i) = 0 을 이용)
대각선을 하나씩 밀면서 채운다는 느낌으로 구하면 된다.
이 알고리즘의 시간복잡도를 구해보면 결국 저 테이블을 모두 채워야 하므로 우선 n² / 2 개의 값을 구해야한다.
이때 하나의 값을 구하는 과정에서 j - i 번의 반복을 돌면서 최소값을 찾으므로 최대 n 의 시간이 걸린다.
따라서 최종 시간복잡도는 O(n³) 이다.
Optimal Binary Search Tree
BST 개념은 자료구조 정리글을 참고하자.
BST는 트리 모양에 따라 그 안에 들어가는 값이 정해진다.
트리 모양으로 가능한 경우의 수는 위에서 설명했듯 카탈란수로 구해진다.
이때 각 key를 탐색하는 빈도가 주어졌을 때, 어떻게 Binary Search Tree 를 구성해야 평균 키값의 비교횟수를 최소로 줄일 수 있을까?
예를 들어 3개 key에 대해 탐색 빈도가 0.3, 0.2, 0.5 로 주어진다고 하자.
그러면 자연스럽게 자주 탐색되는 키를 루트에 두는 것이 더 효율적이라는 생각이 든다.
물론 나이브하게 모든 경우의 수를 구해도 된다.
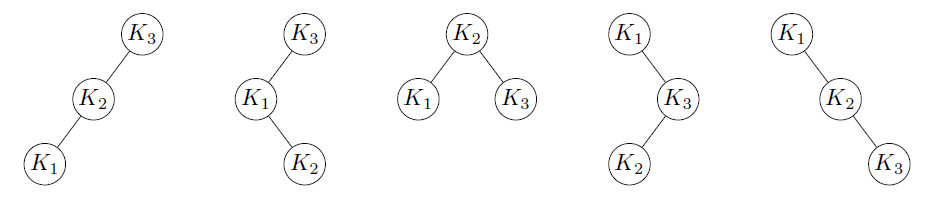
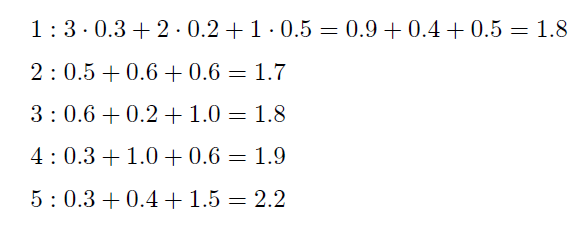
이렇게 비교하는 경우 2번째가 BST가 최적임을 알 수 있다.
또한 어떤 키의 비교 횟수는 그 키가 위치한 트리의 깊이 + 1 임을 알 수 있다.
행렬 곱셈 순서에서 봤던 것처럼, 주어진 문제를 재귀적인 부분 문제로 쪼개면 효율적으로 큰 문제를 풀 수 있다는 것을 알 수 있었다.
마찬가지로 이를 이용해 Optimal Binary Search Tree 문제를 풀어보자.
먼저 BST에서 root는 어떤 키 Ki 를 갖고 있어야 한다.
그리고 왼쪽 서브트리에는 K1 .. Ki-1 의 키가 들어있고, 오른쪽 서브트리에는 Ki+1 .. Kn 의 키가 들어있다.
이때 왼쪽 서브트리 전체에 대한 평균 키값 비교 횟수는 왼쪽 서브트리의 평균 깊이 + 1 로,
오른쪽 서브트리 전체에 대한 평균 키값 비교 횟수는 오른쪽 서브트리의 평균 깊이 + 1로 정해진다.
단, 이때 각 키값의 탐색 빈도를 고려해야 하므로
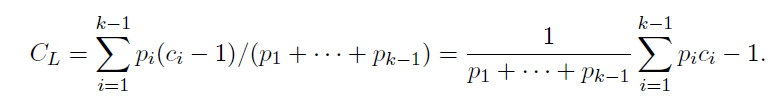
왼쪽 서브트리의 평균 키값 비교 횟수는 위와 같이 정의된다.
(-1은 시그마 공식 밖에 있는 -1 이다.)
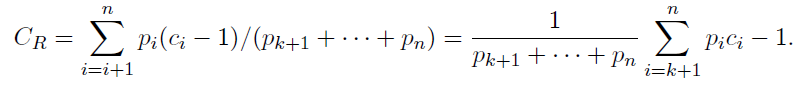
오른쪽 서브트리도 마찬가지로 구해지며 이를 조합하면 전체 평균 키값 비교 횟수는
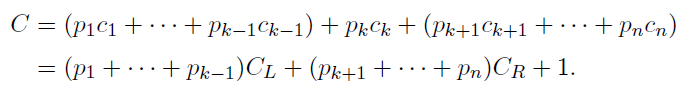
마지막에 +1이 되는 이유는 우선 루트와 먼저 비교해야 하기 때문에 비교횟수가 1이 존재하기 때문이다.
이를 보기 쉽게 i부터 j까지 확률의 합을 P(i, j) 라고 하자.
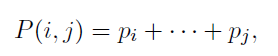
그러면 i, j 까지 키들에 대한 평균 키값 비교횟수는
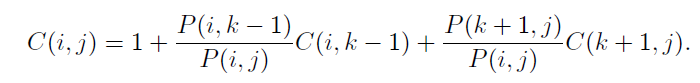
이렇게 구할 수 있다.
왼쪽 서브트리가 선택될 확률 x 왼쪽 서브트리의 평균 키값 비교 횟수
오른쪽 서브트리가 선택될 확률 x 오른쪽 서브트리의 평균 키값 비교 횟수이다.
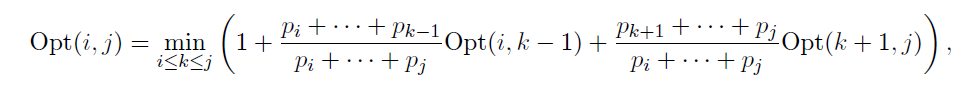
이 평균 키값 비교 횟수의 최적을 구할 땐 이 공식을 그대로 i부터 j 범위에 대해 모두 구해보고, 그 최소 (또는 경우에 따라 최대) 를 취하면 된다.
이때의 base case는
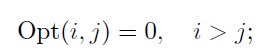
이다.
또는
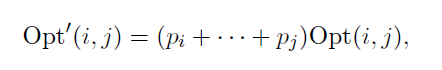
이렇게 opt를 정의하여
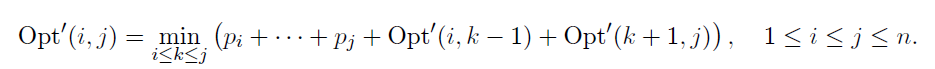
이렇게 점화식을 작성할 수도 있다.
optimal BST 문제의 구성을 보면 행렬곱셈순서와 그 구조가 비슷하다.
따라서 시간복잡도는 O(n³) 이다.
'CS > 알고리즘 분석' 카테고리의 다른 글
| [알고리즘분석] 3. 탐욕법 (Greedy) (0) | 2024.04.23 |
|---|---|
| [알고리즘분석] 1. 분할 정복 (Divide and Conquer) (1) | 2024.04.23 |
| [알고리즘분석] 0. Preliminaries : 덧셈/곱셈 & 피보나치 수열의 시간복잡도 (0) | 2024.04.22 |
