Local Feature Extraction
서로 다른 이미지에서 물체를 매칭하기 위해서, 각 물체의 '특징'을 추출해야 한다.
현대에는 특징점 추출 연산으로 SIFT, SURF 와 같은 연산자를 사용하며, 이들은 스케일 (크기 변봐) , 방향, 밝기 변화에도 불구하고 같은 특징을 갖는 (불변한 값을 갖는) 특징점을 찾는 것을 목표로 한다.
사실 이미지의 특징으로 사용할 수 있는 것 중에 지난 글에서 정리한 방법대로 검출했던 '엣지' 가 있다.
하지만 엣지가 제공하는 정보는 강도와 방향, 2가지에 한정된다.
보다 다양한 정보를 특징으로 사용하기 위해 엣지대신 gray scale 이미지로부터 추출되는 local feature 를 사용하는 방법이 등장했다.

이 이미지는 같은 물체를 서로 다른 방향에서 찍은 이미지이다.
이때 각 물체의 같은 부분을 찍었을 때, 각 이미지에서 이를 확대해보면 밝기가 다르게 나오는 것을 알 수 있다.
Moravec Corner Detection
SSD ( sum of squared difference ) 를 사용해 밝기의 변화를 측정한다.

Input 이미지 f(y, x) 에 대해 w(y, x) 마스크를 씌워서 위와 같이 계산하면 밝기 변화값을 측정할 수 있다.

예를 들어 위와 같은 이미지가 있다고 할 때, 점 b (y = 5, x = 3) 에 대해
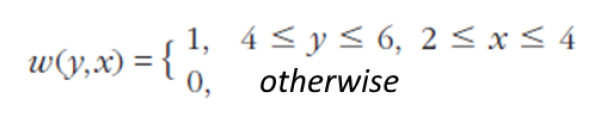
위와 같은 마스크 함수를 적용해서 S(0, 1)을 구하면

위와 같이 계산할 수 있다.
y 값 3가지, x 값 3가지 해서 총 9가지의 조합을 대입해서 구한뒤 다 더하면 된다.
위 이미지의 세 점 a, b, c 에 대해 그 점 주위로 3x3 행렬을 w(y, x) 마스크로 씌운다고 생각해서 s(v, u) 를 구하면 아래와 같이 나온다. (-1 <= v <= 1, -1< = u <= 1)
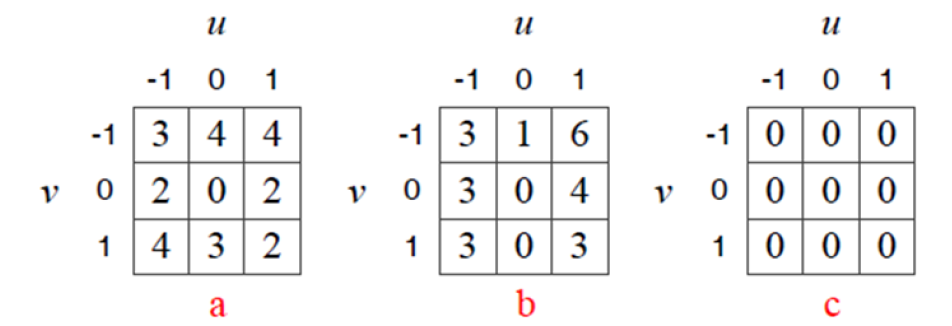
이 값을 분석해보면, c는 모든 방향에서 변화가 없으므로 0이 나오고
b는 가로 방향으로는 변화가 큰데 세로방향으로는 변화가 적고,
a는 모든 방향에 대해 변화가 크다는 것을 알 수 있다.
따라서 이를 이용하면 어떤 점이 그 주변에 비해서 얼마나 다른지를 측정할 수 있다.

다른 예시로서 위 그림을 봐보자.
a 점은 모든 방향에서 변화가 크다.
b 점은 특정 방향에서는 변화가 없다. (엣지 위의 점)
c 점은 모든 방향에서 변화가 없다.
모라벡은 코너를 찾기 위해, 아래와 같이 S(v, u) 를 사용할 것을 제안했다.
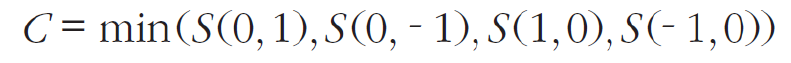
만약 어떤 점(픽셀)이 코너에 있는 점이라면, 모든 방향에 대해 분산이 클 것이다.
따라서 위와 같이 4개의 S(v, u) 값 중의 최소값을 지역 최소 대표값 (local minima candidate) 으로 사용할 수 있다고 주장한다.
하지만 1픽셀 씩 이동하며 측정하는 방식이 충분히 좋은지, s(v, u) 4개 값만 사용해서 4방향만 체크해도 괜찮은 건지 의문을 남긴다.
따라서 이미지 노이즈에 대응하는 것이 좋지 않다.
Harris Corner Detection
해리스는 노이즈에 대처하기 위해, w(y, x) 라는 마스크 대신 가우시안 필터를 적용했다.

따라서 지금 보고 있는 점이 중심으로부터 멀면 작은 값을 갖는다.
또 기존의 모라벡 코너 감지 기법이 1픽셀씩 움직이고, 방향도 4개 밖에 체크하지 않는다는 점에서 isotropic property를 만족하지 않는 문제가 있었기 때문에, 이를 해결하고자 differentiation을 사용했다.

taylor expansion 에 따르면 위와 같이 식을 변형할 수 있는데, d_y, d_x 는 각각 f(y, x) 에 대한 y, x축 미분값이다.
이때 미분을 구하기 위해, x, y 축에 [-1, 0 1] 마스크를 사용하였다
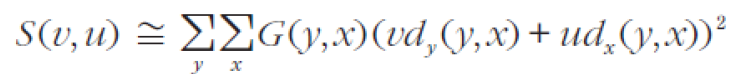
그럼 위와 같이 S(v, u)를 구할 수 있다.

단순하게 표기하기 위해서

이 값을

이렇게 표현한다고 했을 때,

다음과 같이 S(v, u)를 구할 수 있다.

이를 위와 같이 표현할 수 있는데, 여기에서 행렬 A를 2차 모먼트 행렬 또는 Auto-Correction 라고 부른다.
그리고 이 2차 모먼트 행렬로부터 특징점을 구하기 위한 '특성값' 을 다음과 같이 구하도록 했다.


이때 상수 k의 값은 보통 0.04 를 사용한다.
이렇게 구한 C 값중에서, 특정 값 이상의 값만을 추출하면, 위 '사슴 사진' 예제에서는 아래와 같이 픽셀이 골라진다.

그런데 해리스가 제안한 '코너' 를 찾는 이 방식은 사실 '코너'를 찾는데는 어떻게보면 적합하지 않았다.
예를 들어 위사진에서 사슴의 눈과 같은 부분은 코너가 아니기 때문이다.
그래서 사람들은 이런 점들을 '코너' 라고 부르는 대신 '특징점 (feature) ' 이라고 부르기 시작했다.
FAST Corner Extraction

FAST (Features from Accelerated Segemtn Test) Corner Extraction은 어떤 픽셀 주변의 16개 픽셀의 밝기 값을 비교해서 특징점을 찾는 방법이다.
알고리즘 이름에도 나와있듯 굉장히 빠른 속도로 구해진다고 한다.
주변 16개 픽셀의 밝기 값을 비교해서, 9개 이상의 픽셀이 자신보다 충분히 밝거나 어두우면 해당 픽셀을 corner로 인식한다.
만약 현재 보고 있는 점이 Ip의 밝기를 가질 때, 주변 16개 점을 검사해서 그 중 9개 이상이 Ip + t 이상의 밝기를 가지면, (밝을수록 값이 크니까) 나는 주변 점들보다 어두운 점이라는 것을 알 수 있다.
반대로 주변 16개 점을 검사해서 그 중 9개 이상이 Ip - t 이하의 밝기를 가지면, (어두울수록 값이 작아지니까) 나는 주변 점들보다 밝은 점이라는 것을 알 수 있다.
이때 t 값은 코너 여부를 검출하는 기준이 되는, threshold 값이 된다.
FAST는 검출된 코너 (특징점) 주변의 픽셀들을 추출하므로, 비최대 억제를 실행하는 것이 바람직하다.
Scale - Invariant Feature Extraction

물체는 멀리 있으면 흐릿해보이고, 가까이 갈 수록 선명해진다.
인간의 눈은 이렇게 멀리 있는 물체(스케일이 변화)를 보더라도 특징을 인식할 수 있다.
예를 들어 위 산 이미지를 봤을 때, 오른쪽 사진은 10배나 작은 사진임에도 불구하고 '산' 이라는 특징으로서 충분히 인식할 수 있다.
지금까지 Moravec, Harris, FAST 3가지의 특징 추출기를 정리했는데, 과연 이 특징 추출기들도 위와 같이 스케일이 변한 이미지에 대해서 크기가 큰 이미지와 작은 이미지에서 공통된 특징을 추출할 수 있을까?
지금까지 사용한 특징 추출기는 모두 크기가 고정된 이미지에 대해 작용하기 때문에, 공통 특징을 추출하는데 사용할 수 없다. 따라서 다른 특징 추출기가 필요하다.
다른 2개의 이미지에 대해 다른 크기로 표시되는 어떤 물체가 있다.
이 2개의 이미지에 대해 같은 특징을 추출하려면, 규모가 서로 다른 특징 추출 연산자를 사용하면 된다.
하지만 우리는 이미지 규모에 대한 정보를 갖고 있지 않기 때문에 다른 해법이 필요하다.
1. 연산자를 작은 스케일에서 큰 스케일로 점점 증가시킨다.
다양한 크기 스케일에 대한 특징점 집합을 모으기 위해 반복적으로 특징을 구한다.
2. 이미지 해상도를 점진적으로 감소시키면서 다중 스케일 이미지를 구성하고, 이에 대해 동일한 연산자를 적용한다.
즉, 이미지를 고정하고 연산자를 변화시키거나, 연산자를 고정하고 이미지의 스케일을 변화시킨다.

첫번째 방법은 가우시안을 이용해서 점점 흐리게 만든다.
두번째 방법은 이미지 크기를 점점 감소시킨다.
두번째 방법은 임의의 스케일링된 이미지를 처리할 수 없는 특정 스케일이 있다.
따라서 보통은 첫번째 방법을 선호한다.
첫번째 방법을 사용할 때는 원본 영상에 없는 blob나 엣지가 생성되면 안된다.
따라서 가우시안 마스크를 씌워서 이를 방지한다.
N-jet
0차부터 n차까지 도함수를 모은 집합을 말한다.

2-jet은 위와 같은 원소를 가진다.
이떄 각각의 도함수들은 회전에 대해 변하지 않는 값이다.

그래서 이 값들은 회전에 변하지 않는다.
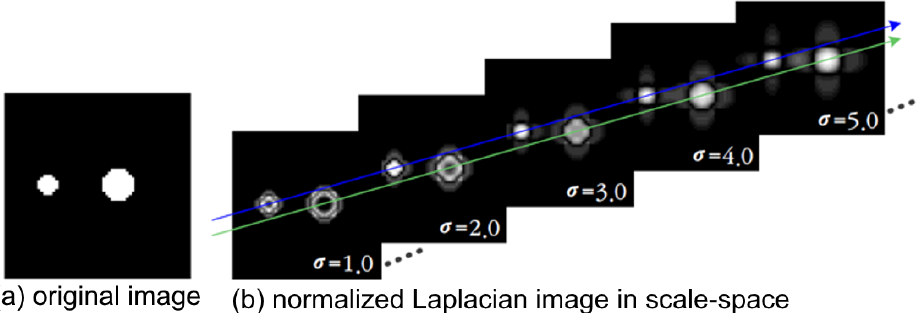
(a) 에서 왼쪽은 지름이 7이고, 오른쪽은 지름이 11인 서로 다른 blob 객체이다.
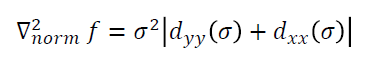
이에 대해 normalized 라플라시안을 적용한 결과는 오른쪽과 같다.
이때 normalize를 하는 이유는, 시그마가 커질 수록 Dyy, Dxx 가 작아지기 때문이다.
위 식에서 Dyy(시그마) 로 표현한 이유가, 시그마로 가우시안 필터를 적용했을 때 Dyy 라는 것을 명시하기 위함이다.

이 그림은 시그마 값에 따라 지름의 크기가 다른 blob에 대해 라플라시안 적용 결과가 어떻게 변하는지를 보여준다.
시그마를 키우면 키울 수록 feature 가 날라가기 때문에 적당히 키운 최적을 찾아야 하는데 blob 이미지 크기에 따라서 그 최적점이 서로 다르다.
스케일 공간을 고려하기 전에, 특징점은 다음과 같은 절차로 구한다.
1. 잠재적 feature map을 구축한다.
2. 각 잠재적 특징점들에 대한 local extrema를 찾는다.
그러나 스케일 변화를 고려하면 위 방법은 잘 통하지 않는다.
스케일 공간에 대한 개념은 이를 극복할 수 있는 대안을 제공한다.
먼저 3D 스케일 공간 (y, x, t) 를 만들고, 이곳에서 extreme point를 찾는다.
그러면 이곳에는 작은 이미지와 큰 이미지 모두에 대한 특징점이 존재할 가능성이 있다.
이제 크기에 상관없이 공통된 특징점을 구하는 방법을 소개한다.
Harris - Laplace Algorithm
이 알고리즘은 2D 이미지 공간(x,y)와 스케일 축 t를 별도로 처리하는 방법이다.
2D 이미지 공간에는 Harris 특징점 검출 방식을 사용한다. (det(A) - k * trace(A)^2)
그리고 스케일 축에 대해서는 normalized 된 라플라시안을 사용한다.
이미지 공간에서 라플라시안은 edge에 대해 극점이 발생하므로, 정규화된 라플라시안을 사용하여 이를 피한다.
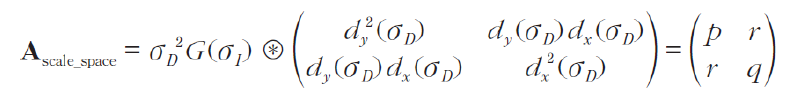
따라서 이를 고려하여 Harris 특징점 검출 방식을 개선하면 위와 같이 사용할 수 있다.
시그마D 값은, 먼저 이미지에 이 값으로 가우시안을 적용했다는 것을 의미한다.
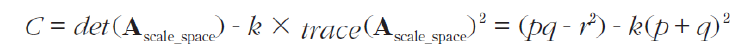
이로부터 크기에 상관없이 공통된 특징을 갖는 특징점을 위 식으로 검출할 수 있다.
SIFT
SIFT 는 Scale-Invariant Feature Transform 의 줄임말로, 최근 가장 효과가 좋다고 알려진 특징점 추출 알고리즘이다.
이 알고리즘을 사용하면 local feature에 대해 반복적으로 사용할 수 있다는 장점이 있다.
그리고 연산 속도도 굉장히 빠르다고 한다.
'CS > HCI 윈도우즈프로그래밍' 카테고리의 다른 글
| [Computer Vision] 7. Matching & Geometrical alignment (0) | 2024.06.11 |
|---|---|
| [Computer Vision] 5. Edge Detection (0) | 2024.06.07 |
| [Computer Vision] 4. Geometry Primer (3) : Transform (0) | 2024.06.02 |
| [Computer Vision] 3. Geometry Primer (2) : Homography (0) | 2024.05.31 |
| [Computer Vision] 2. Geometry Primer (1) : Homogeneous Coordinates (3) | 2024.05.31 |
