Grammar 에 대해서 어떤 문법의 모든 production 이 A → xB 또는 A → x 형태로 작성된다면,
이 grammar에 대해 right-linear 하다고 말한다. (A, B는 변수이고 x는 터미널이다.)
반대로 모든 production 이 A → Bx 또는 A → x 로 형태로 작성되면,
이 grammar에 대해 left-linear 하다고 말한다.
이때 left-linear 또는 right-linear 한 grammar를 가리켜, Regular Grammar 라고 말한다.
regular grammar는 프로덕션이 만드는 sentential form의 변수 개수가 1개 또는 0개라는 특징이 있다.

위 그림과 같은 2개의 문법을 보자.
production 에 집중해서 보면,
첫 번째 문법은 right-linear 하므로 regualr grammar 이다.
두 번째 문법은 각 프로덕션에 대해 변수가 1개 이하이고 모두 왼쪽에 있으므로 left-linear 해서 regualr grammar 이다.

반면, 이 문법을 보면 화살표 오른쪽의 변수 개수는 1개 이하가 맞지만, 어떨 때는 왼쪽에 있고 어떨 때는 오른쪽에 있기 때문에 regular grammar 라고 할 수 없다.
하지만 이런 문법은 linear grammar 라는 분류로 들어갈 수 있다.
linear grammar 는 화살표 오른쪽에 있는 변수의 개수가 1개 이하이면 위치에 상관없이 성립한다.
그리고 이 정의를 보면 자연스럽게 linear grammar 안에 regular grammar 가 포함되는 관계라는 것을 알 수 있다.

다음 정리는 right-linear grammar로 만들어지는 언어 L(G) 는 regular language 임을 나타낸다.
모든 변수가 오른쪽에 있기 때문에, 각 변수를 state로 매핑하면 NFA를 쉽게 그려낼 수 있기 때문이다.

그림으로는 이렇게 나타낼 수 있다.

만약 터미널에 대한 production 이라면 이렇게 final state로 나타내면 된다.

따라서 다음 예제를 보면, 이 문법이 만드는 언어를 동일하게 만드는 FA를 만들어보면
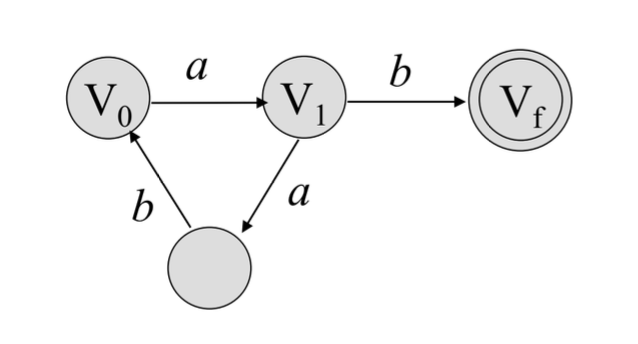
right-linear 한 프로덕션들을 이렇게 그려낼 수 있다.
이때 이런 문제를 풀 때는 문법의 전체 정의를 보고 Start Variable을 꼭 init state로 표시해주어야 한다.

이에 대해서는 역도 성립한다.
만약 어떤 언어가 regular 하다면, 그 언어를 right-linear grammar G를 사용하여 L(G)로 표현할 수 있다.
증명은 거꾸로 하면된다.
어떤 언어가 regular 하다는 것은 NFA가 존재한다는 것이다.
이 NFA의 각 상태와 입력 심볼을 토대로 그대로 production으로 옮겨주면 right-linear grammar로 표현할 수 있다.

이때 중요한 것은, final state 로 가는 transition 을 production 으로 나타낼 때는 그 production에 더해
final state를 나타내는 변수가 λ 로 produce 되도록 하는 production 을 꼭 추가해야 한다.

간단하게 예시를 하나 보면
aab*a 라는 regular expression 을 통해 만드는 언어를 right-linear grammar로 표현해보면
먼저 이를 기반으로 NFA를 그린 뒤 각 트랜지션 함수를 production 으로 바꿔주면 된다.
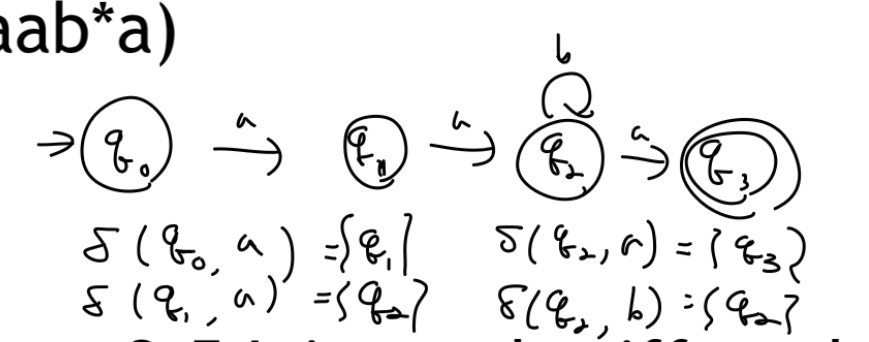
먼저 NFA는 이렇게 그릴 수 있고, 각 트랜지션 함수는 위와 같다. (NFA 이므로 집합 기호로 표시하였다.)

각 트랜지션 함수를 프로덕션으로 표현하면 문법은 어렵지 않게 만들 수 있다.
이때 final state 에 대해서는 꼭 λ 로 프로듀스하는 프로덕션을 만들어야 하는 것에 주의하자.
이게 없으면 항상 sentential form 에서 끝나기 때문이다.

그리고 위와 비슷한 논리를 통해서 left-linear 에 대해서도 같은 설명을 할 수 있다.
regular language를 left-linear 문법으로 나타낼 수 있고, left-linear 문법을 가지고 만드는 언어는 regular 하다.
'CS > 오토마타' 카테고리의 다른 글
| [오토마타] 11. Non-Regular Language 판별 (0) | 2024.10.24 |
|---|---|
| [오토마타] 10. Regular Language 의 Closure Properties (0) | 2024.10.24 |
| [오토마타] 8. Regular Expression 과 Regular Language (0) | 2024.10.23 |
| [오토마타] 7. Regular Expression (0) | 2024.10.23 |
| [오토마타] 6. FA 에서 state 개수 줄이기 (0) | 2024.10.22 |
