regular language는 수학적으로 문장의 집합이다.
regular language는 DFA, NFA로 나타낼 수도, Regular expression 으로 나타낼 수도, Regular Grammar로도 나타낼 수 있다.
그렇다면 우리가 수학적으로 다룰 수 있는 언어는 레귤러 랭귀지가 전부일까?
또한 레귤러 랭귀지에 대한 특정 연산에 대해서 닫힌 (closure) 연산 이 존재할까?
어떤 연산이 닫혀있다는 것은 피연산자와 연산 후 결과의 집합이 같은 것을 말한다.
예를 들어 두 정수를 더하면 그 결과 역시 정수이므로 정수는 덧셈에 대해 닫혀있다고 할 수 있다.
이번 글에서는 Regular Language 에 대해 Closure Properties 에 집중해서 정리해본다.
기본 연산에 대해

위 정리는 두 regular language에 대해, 합집합, 교집합, concatenate, 여집합, star-closure 연산은 모두 닫혀있음을 말한다.
(닫혀있다는 것은 위 연산의 결과 역시 regular language 라는 것이다.)
이 연산들은 모두 regular expression 의 정의로부터 증명할 수 있다.
L1 = L(r1)
L2 = L(r2)
일 때, 두 언어의 합집합은 regular expression 의 정의에 의해 L(r1 + r2) 로 나타낼 수 있는데, r1 + r2 역시 regular expression 이므로 합집합 연산을 적용한 언어 역시 regular 하다.
concatenate 의 경우, r1 r2 가 regular expression 이므로 regular language 이고,
star-closure 역시 r1* 가 regular expression 이므로 regular language 이다.
여집합의 경우, Σ* - L1 과 같다.

이는 이 언어를 나타내는 DFA M에 대해 그 여집합을 나타내는 언어 역시 DFA로 나타낼 수 있다.
final state 와 non-final 를 바꾸면 되기 때문이다.
언어 사이의 관계를 집합으로 표현했을 때

위 그림과 같이 표현할 수 있기에 사용가능한 증명이다.
두 regular language 의 교집합 연산이 닫혀 있는 것은, 합집합, 여집합 연산에서의 증명을 활용하여

이렇게 드모르간의 법칙을 통해 증명할 수 있다.

한번 예시 문제로, 차집합 연산에 대해서도 regular language가 닫혀있는지 확인해보자.

차집합은 여집합과의 교집합으로 나타낼 수 있으므로, 차집합 역시 regular 하다.

정리 4.2는 어떤 언어를 구성하는 모든 문장을 뒤집은, reversal 연산을 취한 regular language 에 대해서도 regular 함을 나타낸다.
이건 기존의 문장을 나타내는 기계 M에 대해 init state와 final state를 바꾸고 모든 엣지의 방향을 뒤집으면 여전히 DFA 이므로 regular 하다는 것을 알 수 있다.
Homomorphism 에 대해
이제 Homomorphism 이라는 개념을 새로 정의한다.
이 개념은 substitution 이라고도 부르는 개념으로, 다음과 같이 정의한다.

homomorphism 은 알파벳과 알파벳으로 구성된 함수로서,
어떤 문장 w를 a1 a2 ... an 의 알파벳으로 나타낼 수 있다면 h(w) = h(a1) h(a2) ... h(an) 로 나타낼 수 있다.
(이때 a 가 속한 알파벳 집합과 h(x) 만드는 문장을 구성하는 알파벳은 서로 다를 수 있다.)
이때, homomorphism 에는 문자열이 들어갈 수도 있다.
만약 문자열이 들어가면 이때는 심볼 바이 심볼로 함수를 적용해서 concatenate 한 것과 같다.
만약 언어가 homomorphism에 들어가면, 그 언어를 구성하는 모든 문자열에 homomorphism을 적용한 새로운 문장의 집합과 같으며 이를 가리켜 homomorphism image 라고 부른다.
따라서 정리를 해보면 homomorphism 에는 심볼을 넣으면 스트링, 스트링을 넣으면 스트링, 언어를 넣으면 언어가 나오는 집합이라고 말할 수 있다.

간단한 연습 문제를 풀어보자.
homomorphism 의 정의가 위와 같이 주어졌을 때, h(aba), h(L) 을 구해보면
h(aba) = h(a) h(b) h(a) = ab bbc ab
h(L) = { h(aa), h(aba) } = { abab, abbbcab }

이번엔 이 문제를 풀어보자.
이 문제는 직관적으로 L(r) 에 대해서 저 정규표현식의 a, b 를 homomorphism이 정의하는 대로 치환해서 적용하면 되는 것을 알 수 있다.
따라서 r1 = (dbcc + (bdc)*)(dbccdbcc)* 으로 적을 수 있다.
이 문제를 통해서 다음 정리를 자연스럽게 이해할 수 있다.

만약 L 이 regular language 라면, h(L) 역시 regular 하다.
따라서 regular language 는 homomorphism에 대해서도 닫혀있다.
Right Quotient 에 대해
마지막으로 Right quotient 라는 개념을 정리해보자.

같은 알파벳으로 구성된 L1, L2 에 대해서, L2를 구성하는 문장 일부가 L1의 모든 문장의 suffix를 나타낼 때,
그 suffix 를 제외한 나머지 문자열로 구성된 집합을 L1 / L2 로 나타내며, 이를 right quotient 라고 한다.
예를 들어 L1 = { hooray, sunray, xray, ray } 라고 하고, L2 = { ray } 라고 하면
L1 / L2 = { hoo, sun, x, λ } 가 된다.
L1 의 모든 문장에서 ray 라는 suffix 를 빼는 것과 같다.
(데이터베이스 관계대수에서 배웠던 디비전 연산과 유사한 느낌이다.)
또 다른 예시로 L1 = { aⁿ bⁿ cⁿ : n ≥ 0 } , L2 = { bⁱ cʲ : i, j ≥ 0 } 가 주어졌을 때, L1 / L2 를 계산해보면

위와 같이 나타낼 수 있다.
이렇게 L2 가 집합의 연산으로 표현되는 경우, L2 의 집합 중에서 L1 의 suffix를 나타내는 문장이 있다면 suffix를 지운 나머지도 포함된다.
예를 들어 L1 = { 0100, 1011, 111 } , L2 = { 100, 11 } 이라면
100 을 suffix 로 갖는 L1 의 문장들에 대해 지우고 남은 나머지를 원소로 취해주면 0100 에 대해 0 이 남으니 0이 추가되고
11 을 suffix 로 갖는 L1 의 문장들에 대해 지우고 남은 나머지를 원소로 취해주면 1011, 111 에 대해 각각 10, 1 이 남아서 추가된다.
따라서 L1 / L2 = { 0, 10, 1 } 이다.
다시 위 예제로 돌아오면 결국 L2 에 속한 문장들로 L1 의 suffix 를 지워낸다면,
a 는 무조건 남을 것이고, b, c 가 모두 지워지거나, b 는 남고 c가 모두 지워지거나, a, b 는 그대로 남고 c만 일부 지워지는 경우로 나눠진다.
b, c 가 모두 지워지는 경우, b는 남고 c가 모두 지워지는 경우는 p >= q and r = 0 조건을 통해 나타낼 수 있고
a, b는 남고 c만 일부 지워지는 경우는 p = q >= r 을 통해 나타낼 수 있다.
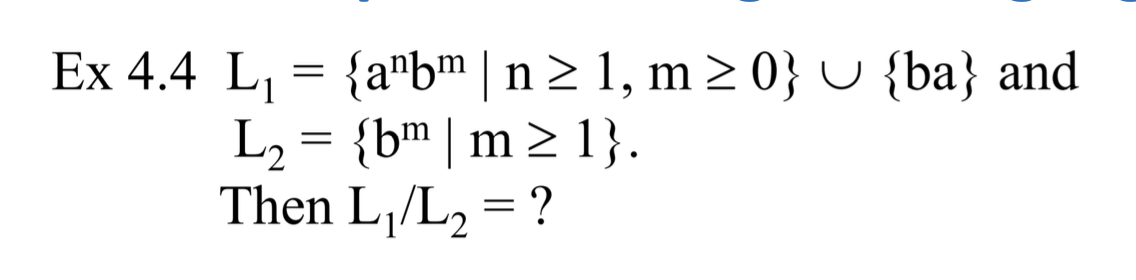
연습 문제를 하나 풀어보자.
먼저 L1, L2 는 regular 하다고 말할 수 있을까?
L1, L2 모두 유한개의 상태를 가진 기계로 표현할 수 있으므로 regular 하다.
L1 을 상태 기계로 나타내면 아래와 같다.

이때, L1 / L2 의 의미를 조금 살펴보면, L2 가 L1 의 suffix를 제외하고 남은 나머지가 L1 / L2 이므로

다음 그림과 같이 나타낼 수 있다.
이때 L2 의 범위 왼쪽에 남아있는 영역이 L1 / L2 가 나타내는 영역이다.
이를 그래프의 상태 관점에서 보면,

이렇게 나타낼 수 있다.
L1 / L2 가 나타내는 언어를 L1 을 나타내는 DFA를 빌려서 표현하면,
q0 상태에서 출발해서 ? 상태를 final state로 하는 문장들인데,
이 ? 상태들에서 시작해서 L1 의 final state로 갈 수 있는 문장들은 L2 에 속하는 문장이다.
따라서 L1 / L2 가 나타내는 언어를 DFA로 그린다면 L1 의 DFA를 구성하는 상태들 중 ? 상태가 될 수 있는 상태들을 final state로 표시한 DFA라고 할 수 있다.
이제 이 DFA를 조금 더 일반화된 generalized transition graph 관점에서 생각하면,
? 상태에서 bb* 라는 L2의 regular expression 만큼 추가적으로 이동하면 L1 의 문장이 된다.
이제 L1 의 DFA를 구성하는 모든 상태들에 대해 그 상태에서 bb* 만큼 이동했을 때 final state로 갈 수 있는지 확인해보면
q0 에서는 bb* 만큼 이동했을 때 final state로 갈 수 없다. 따라서 q0 는 ? state가 될 수 없다.
q1 에서는 bb* 만큼 이동했을 때 final state로 갈 수 있다. 따라서 q1 은 ? state가 될 수 있다.
q2 에서는 bb* 만큼 이동했을 때 final state로 갈 수 있다. 따라서 q2 는 ? state가 될 수 있다.
q3, q4, q5 는 될 수 없다.
따라서 ? 에 해당하는 state인 q1, q2 만을 final state로 갖는 DFA로 만들면 이 DFA가 만드는 언어가 L1 / L2 가 된다.

이 DFA가 L1 / L2 를 나타내는 최종 DFA 이다. (기존 DFA 에서 q4 가 non final 로 변했다.)

다른 연습 문제를 풀어보자.
주어진 그림은 L1 의 DFA를 나타낸다.
이때 L2 라는 언어가 정규 표현식 형태를 통해 정의되어있다.
L1, L2 가 모두 정규표현식으로 정의되어 있으므로 두 언어는 regular language 이다.
L1 / L2 를 찾기 위해서 위에서 했던 과정을 다시 반복해보자.
q0 에서 ab* 만큼 이동하는 경우, q2로 갈 수 없다. 따라서 q0 는 ? state가 될 수 없다
q1 에서 ab* 만큼 이동하는 경우, q2로 갈 수 있다. (b를 사용하지 않으면 된다.) 따라서 q1 은 ? state 가 될 수 있다.
q2 에서 ab* 만큼 이동하는 경우, q2로 갈 수 있다. (b를 사용하지 않으면 된다.) 따라서 q2도 ? state 가 될 수 있다.
q3 에서 ab* 만큼 이동하는 경우, q2로 갈 수 없다. 따라서 q3 은 ? state 가 될 수 없다.
따라서 L1 / L2 를 만드는 문장은 위 DFA에서 q1, q2 만을 final state로 갖는 DFA 이다.
그리고 이 과정을 통해서 L1 / L2 를 구하다보면 자연스럽게 알 수 있는 것이,
L1, L2 가 regular 하다면, L1 / L2 도 regular 하다.
즉, regular language 는 right quotient 에 대해서 닫혀있다고 할 수 있다.
'CS > 오토마타' 카테고리의 다른 글
| [오토마타] 12. Toy Program for DFA (0) | 2024.12.04 |
|---|---|
| [오토마타] 11. Non-Regular Language 판별 (0) | 2024.10.24 |
| [오토마타] 9. Regular Grammar (0) | 2024.10.23 |
| [오토마타] 8. Regular Expression 과 Regular Language (0) | 2024.10.23 |
| [오토마타] 7. Regular Expression (0) | 2024.10.23 |
