Regular Language 의 특성 판별

어떤 regular language 에 임의의 문자열을 넣었을 때, 그 문장이 L에 포함되는지 안되는지 결정할 수 있는 알고리즘이 존재한다.
너무나도 당연한 말이다.
왜냐하면 regular language 는 DFA를 통해 나타낼 수 있고, 이 기계에 문자열 w를 넣으면 이 문장이 L 에 속하는지 판별할 수 있기 때문이다. DFA는 곧 판별 알고리즘을 나타내는 것과 같으며, 이런 알고리즘을 가리켜 membership algorithm 이라고 한다.

standard representation 으로 나타낸 regular language 에 대해서, 이 언어 집합이 공집합, 유한집합, 무한집합 중 어떤 것에 해당하는지 판별하는 알고리즘이 존재한다.
1. 공집합 여부 판단
DFA 트랜지션 그래프로 언어를 나타낸 뒤, init state 에서부터 final state로 가는 하나의 경로가 존재하는지 여부로 판단할 수 있다.
2. 무한집합 여부 판단
DFA 트랜지션 그래프는 반드시 유한개의 상태만을 갖는다.
그런데 이 그래프가 무한히 많은 언어를 나타내려면 상태를 1번씩만 거쳐서는 절대 나타낼 수 없다.
즉, 여러 상태를 반복적으로 방문할 수 밖에 없고, 그 말은 사이클이 있다는 뜻과 같다.
따라서 DFA 를 트랜지션 그래프로 나타냈을 때, init state 에서 final state로 가는 경로에 사이클의 base vertex 가 포함이 되는 경우가 존재하면 무한집합이고, 아니면 유한 집합이다.

두 regular language L1, L2 가 주어졌을 때, 두 언어가 같은지 판별할 수 잇는 알고리즘이 존재한다.
언어는 결국 집합이다.

L3 라는 새로운 집합을 기존의 L1, L2 집합의 연산을 통해 ( L1 - L2 ) ∪ ( L2 - L1 ) 이라고 정의해보자.
L1 과 L2 가 같다면 이 연산의 결과는 공집합이고, L1 과 L2가 다르다면 이 결과는 공집합이 아니다.
이때 L1, L2 가 모두 regular 하며, regular language 는 합집합, 차집합 연산에 대해 닫혀있으므로 이 연산 결과인 L3 역시 regular language 이다.
그런데 바로 직전 정리에서 우리는 regular language 가 공집합인지 아닌지 판별할 수 있음을 증명하였다.
따라서 L3 에 대해서 공집합인지 아닌지 판별할 수 있고, 이를 토대로 L1, L2 가 같은 언어를 나타내는지 판별할 수 있다.
Non-Regular Language 판별
비둘기집 원리
언어라는 집합을 유한 집합과 무한 집합으로 분류할 때, 유한집합에 대해 먼저 생각해보자.
유한 개의 문장으로 구성된 언어는 regular 할까? 정답은 regular 하다.
문장이 유한 개라는 것은, 각 문장이 될 때 final state가 되도록 하는 모든 유한가지 경우의 수를 만들어서 NFA를 그릴 수 있기 때문이다.
그리고 NFA는 DFA로 고칠 수 있고, DFA가 존재하는 언어는 regular 하다.
따라서 어떤 언어가 regular 한지 non-regular 한지 판별하는 것은
'무한 개의 문장을 가진 언어'에 대해 고민하는 것으로 한정할 수 있다.
무한 개의 문장으로 구성된 언어의 regular 여부를 따질 때는 비둘기집 원리가 유용하게 사용된다.

비둘기집 원리는 간단하다.
비둘기집이 m 개 있고, m < n 인 n 마리의 비둘기가 있을 때, 모든 비둘기가 비둘기 집에 들어가야 한다면 최소한 1개의 비둘기 집에는 2마리 이상의 비둘기가 존재할 수 밖에 없다는 원리이다.
이를 조금 더 일반적으로 확장해서 비둘기의 집이 유한 개 있는데, 비둘기가 무한 마리가 있다고 해보자.
이때도 반드시 최소 1개의 비둘기 집에는 2마리 이상의 비둘기가 존재할 수 밖에 없다.
이 원리를 DFA 에 그대로 적용해보자.
DFA는 유한 개의 상태를 가진 기계이며, DFA로 들어오는 문장은 DFA에 존재하는 상태 중 하나로 결정되어 속한다.
이때 어떤 언어의 문장이 무한한 상황이라면, 마치 유한 개의 비둘기집에 무한 마리의 비둘기를 담는 것처럼, 유한개의 상태에 무한개의 문장을 각 상태에 나누어 담는다고 생각할 수 있다.
그러면 비둘기집 원리에 따라, 적어도 하나의 상태는 여러 개의 문장에 대해 언어에 속하는지 여부를 판별할 수 있다.
즉, 서로 다른 문자열이 같은 상태에 도달할 수 있다는 것이다.
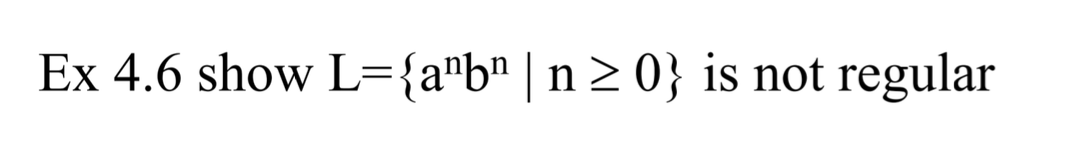
이 원리를 토대로 위 문제를 풀어보자.
주어진 언어 L 은 regular 하지 않다.
먼저 직관적으로는, a, b 의 개수가 '동일해야' 한다.
a, b 의 개수가 동일하다는 것을 DFA로 판별하려면 각 a, b 의 정확한 개수를 카운팅하여 각각에 대해 상태를 갖고 있어야 한다.
하지만 n ≥ 0 이면 n 값은 무한가지가 될 수 있고, 이 개수를 카운팅하려면 무한 개의 state 가 필요하므로 DFA 로는 나타낼 수 없다.
따라서 이 언어는 regular language 가 아니다.
비둘기 집의 원리를 적용한다면, 어떤 문자열 심볼들이 쭉쭉 주어질 때, 처음에 a 가 무한개가 주어질 수 있다.
그런데 DFA의 상태는 유한하므로 적어도 1개의 상태가 여러개의 a 입력을 동시에 받아들인다.
이때 여러 개의 a 입력을 받아들이는 상태가 aⁿ 도 받아들이고 aᵐ 도 받아들인다고 해보자. ( n ≠ m)
만약 aⁿ 을 받아들였다면 이후에 bⁿ 을 받아들였을 때 final state로 가야할 것이다.
그런데 이 상태에서 aᵐ 을 받아들였을 때 bⁿ 을 받아들이면 이번엔 non-final state 로 가야한다.
즉, 같은 상태에서 같은 입력이 주어졌는데 어디로 갈지 결정할 수 가 없어서 이는 DFA가 될 수 없으니 모순이다.
A Pumping Lemma
무한 개의 문장을 갖는 언어가 regular 한지 non-regular 한지 판별할 때 pumping lemma 가 사용될 수 있다.
어떤 언어에 속하는 '충분한 길이의 문장' w 는 w = xyz 라는 형태로 3조각을 낼 수 있다.
이때 x, y, z 라는 각 조각에 대해서 가운데에 있는 y 조각을 pumping up, pumping down 할 수 있다는 것이 pumping lemma 이다.
만약 y 조각을 pumping down 하면 y⁰ = λ 이 되어 xz 로 구성된 문자열이 될 것이고,
만약 y 조각을 pumping up 하면 y² 로 증가하여 xy²z 로 구성된 문자열이 될 것이다.
이때 만약 주어진 언어 L 이 regular 하다면, xy 도 xy²z 도 모두 L의 문장이다.
즉, 몇 번의 펌핑 업, 다운을 하든 그 결과로 나오는 모든 문자열은 L의 문장이다.

먼저 어떤 regular language를 나타내는 DFA가 있다고 해보자.
이 DFA는 q0 부터 qn 까지 n+1 개의 상태를 가진다.
만약 이 DFA 에 길이가 1인 문자열을 넣는다면, init state → another state 이렇게 한번의 transition 이 발생하고,
2개의 state를 사용하여 주어진 문자열이 문장인지 판별한다.
이때 거쳐가는 state를 나열하면 그 길이는 2이다.
만약 이 DFA 에 길이가 2인 문자열을 넣는다면, 2번의 transition 이 발생하고, 3개의 state 를 사용하여 주어진 문자열이 문장인지 판별한다. 이때 거쳐가는 state를 나타내면 그 길이는 3 이다.
만약 길이가 n + 1 인 문자열을 넣는다면, 이 문자열이 문장인지 판별할 때는 n + 1 번의 trainsition 이 발생하고, n+2 번의 state를 사용하여 주어진 문자열이 문장인지 판별한다. 즉, 이때 거쳐가는 state를 나열하면 그 길이는 n + 2 이다.
만약 이 문자열이 문장이라면, 최종 도착하는 state 는 final state 이다.
그런데 이 DFA에는 총 n+1 개의 state가 존재하고 있다.
그러면 이 문장을 판별하는데 n+2 번이 상태를 거쳐갔으니 비둘기집 원리에 의해 적어도 한번의 상태는 중복 방문하였음을 알 수 있다.
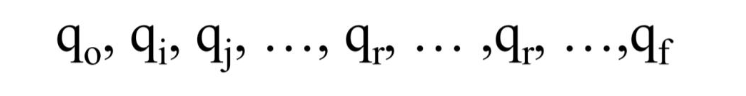
이때 중복 방문하는 state 를 가리켜 qr 이라고 해보자.
그리고 이 qr은 여러번 반복되므로, 처음 등장하는 순서와 마지막에 등장하는 순서를 seq 에서 위와 같이 표현하였다.
이제 이 seq를 3분할 해보면 다음과 같이 나눌 수 있다.
이때 y 시퀀스의 길이는 1 이상이고, xy 시퀀스의 길이는 n+1 이하이다.
왜냐하면 xy 시퀀스는 아무리 길어져도 모든 상태 n+1 개를 다 방문한 다음에는 qr이 한번 더 등장할 수 밖에 없기 때문이다.

이 상태 방문 sequence를 extended thransition function 으로 나타내면

이렇게 나타낼 수 있다.

그러면 이를 정리하여 위와 같이 나타낼 수 있다.
따라서 충분히 긴 문장을 받아들이는 regular language 라면, 3분할을 했을 때 y² 과 같이 반복적으로 방문하는 상태가 존재할 수 밖에 없으며, 그 말은 그 상태로 돌아오는 사이클이 존재할 수 밖에 없다.
pumping up 을 하면 이 사이클을 더 많이 도는 것이고, pumping down 을 하면 이 사이클을 돌지 않는 것이 된다.

예를 들어 이 언어를 NFA로 표현하면 위와 같다.
이 NFA는 4개의 상태로 구성되어 있으므로 m = 4 라고 하면, |xy| <= m = 4 이다.
또 이 언어의 문장 중에서 길이가 m = 4 이상인 문장은 모두 3조각을 낼 수 있다.

길이가 4인 문자열 중 하나를 뽑으면 abbb 가 존재한다.
이 문자열을 만드는 state 변화 seq를 나타내면 위와 같이 5개의 state로 나타낼 수 있고,
이를 3분할 하면 x = λ, y = a, z = bbb 로 쪼갤 수 있다.
왜냐하면 y 는 pumping up, down 이 가능해야하는데, 이 seq 에서 사이클은 q0 - q0 로 가는 state 밖에 없기 때문이다. 이 구간을 정해두고 나면 나머지 앞 뒤가 x, z 가 된다.
따라서 이 케이스는 |xy| = 1 인 극단적인 케이스를 보여준다.
이런 케이스가 등장하는 이유는 regular expression 맨 앞에서 * 가 등장했기 때문이다.

이번에는 |xy| = m 이되는 케이스를 살펴보자.
주어진 문장의 정규 표현식을 NFA로 나타내면 위와 같고, 4개의 state로 구성되어 있으니 m = 4 이다.
따라서 m = 4 이상의 문자열에 대해서 이 문자열은 반드시 쪼갤 수 있고, |xy| <= 4 이다.
이 언어에 속하는 문장 중 하나인 aaaba를 가져오면 이 문장을 넣었을 때 상태변화는 6개의 상태로 나타낼 수 있다.
이 중에서 cycle이 발생하는 경우는 q2-qf-q2 이며 이 부분을 y로 묶은 뒤 앞 뒤를 x, z 로 만든다.
이렇게 보는 것처럼 극단적으로 *를 맨 뒤에 붙이면 |xy| = m = 4 로 최대가 된다.
이제 pumping lemma를 사용하여 어떤 문장이 non-regular 하다는 것을 판별해보자.
이때 주의할 점은 regualr language 와 pumping lemma 는 서로 왔다갔다 할 수는 없다.

어떤 언어가 regular language 라면, pumping lemma를 적용하여 3분할 후 up, down 해도 여전히 regular language 이지만,
어떤 언어에 대해 pumping lemma 를 적용하여 3분할 후, up, down 해도 여전히 같은 language 라고 해서 그 언어가 regular 하다고는 말할 수 없다.
그러면 pumping lemma는 어떤 언어가 regular 인지 non-regular 인지 판별할 때 어떻게 활용할 수 있을까?

언어에 대해 다음과 같은 집합 관계가 성립한다.
언어 안에는 pumping lemma가 적용되는 언어가 있고, 그 안에는 무한개의 문장을 갖는 Regular language 가 있다.
따라서 우리가 판별하려는 어떤 언어 Lx 가 pumping lemma 영역 밖에 있다면, 적어도 이 언어는 regular 하지는 않다고 판별할 수 있다.
그래서 주어진 언어가 non-regular 한지 판별하는 것은 귀류법을 사용하여 다음과 같은 과정을 거친다.
1. 주어진 언어가 regular 하다고 가정한다.
2. 주어진 언어가 regular 하므로 이 언어를 만드는 DFA 에 대해 어떤 상태는 반드시 반복된다.
3. 그 상태를 기준으로 어떤 문장을 xyz 로 쪼갠 뒤, y 에 대해 pumping 하고 그 pumping을 했을 때는 그 문장이 L에 속하지 않음을 보인다. (L에 속하지 않다면 pumping lemma가 적용되지 않으므로 DFA라는 초기의 가정은 틀렸음을 알 수 있다.)
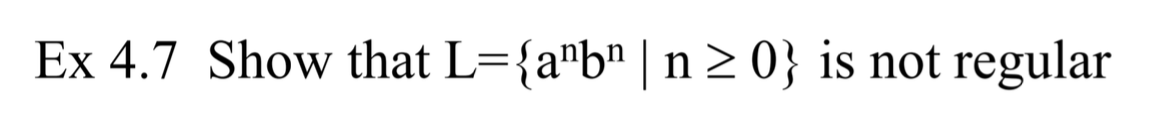
연습 문제를 풀어보자.
이때 위 증명 과정을 마치 두 명의 상반된 의견을 가진 사람이 논쟁하는 것처럼 묘사해볼 수 있다.

1. 먼저 주어진 언어가 regular 하다고 믿기에, pumping lemma가 될 것이라고 믿는 상대방은 충분히 긴 길이가 m인 문장하나를 뽑아서 나에게 제시한다.
2. 나는 그것보다 더 긴 길이가 2m 인 문장을 뽑아서 상대방에게 xyz로 쪼개보라고 제시한다.
(주어진 언어에서 길이가 2m 이려면 aᵐbᵐ 일 것이다.)
3. 상대방은 내가 제시한 문장을 xyz로 쪼갠다. 이때 최대한 자신에게 유리하도록 쪼갤 것이다.
상대방은 y = aᵏ 를 뽑을 수 밖에 없다. (1 <= k <= m, |y| >= 1, |xy| <= m 이기 때문에 a 영역에서 밖에 못 고른다.)
4. 상대방이 쪼갠 xyz에 대해 y를 자유롭게 늘리고 줄이면서 L에 속하지 않는 문장을 찾는다.
만약 y 를 pumping down 하여 제거한 경우, 남은 문장 xy 는 aᵐ⁻ᵏbᵐ 이다.
이때 k >= 1 이므로 m - k ≠ m 이다. 따라서 xy 는 L에 속하는 문장이 아니므로 pumping lemma 가 적용되지 않는다.
따라서 주어진 언어는 non-regular 하다.
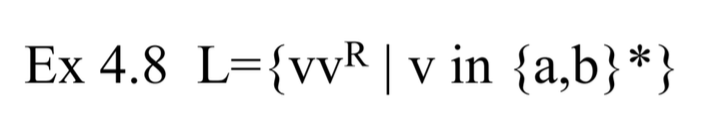
다른 연습 문제를 풀어보자.
주어진 문장이 non-regular 한지 판별해보자.
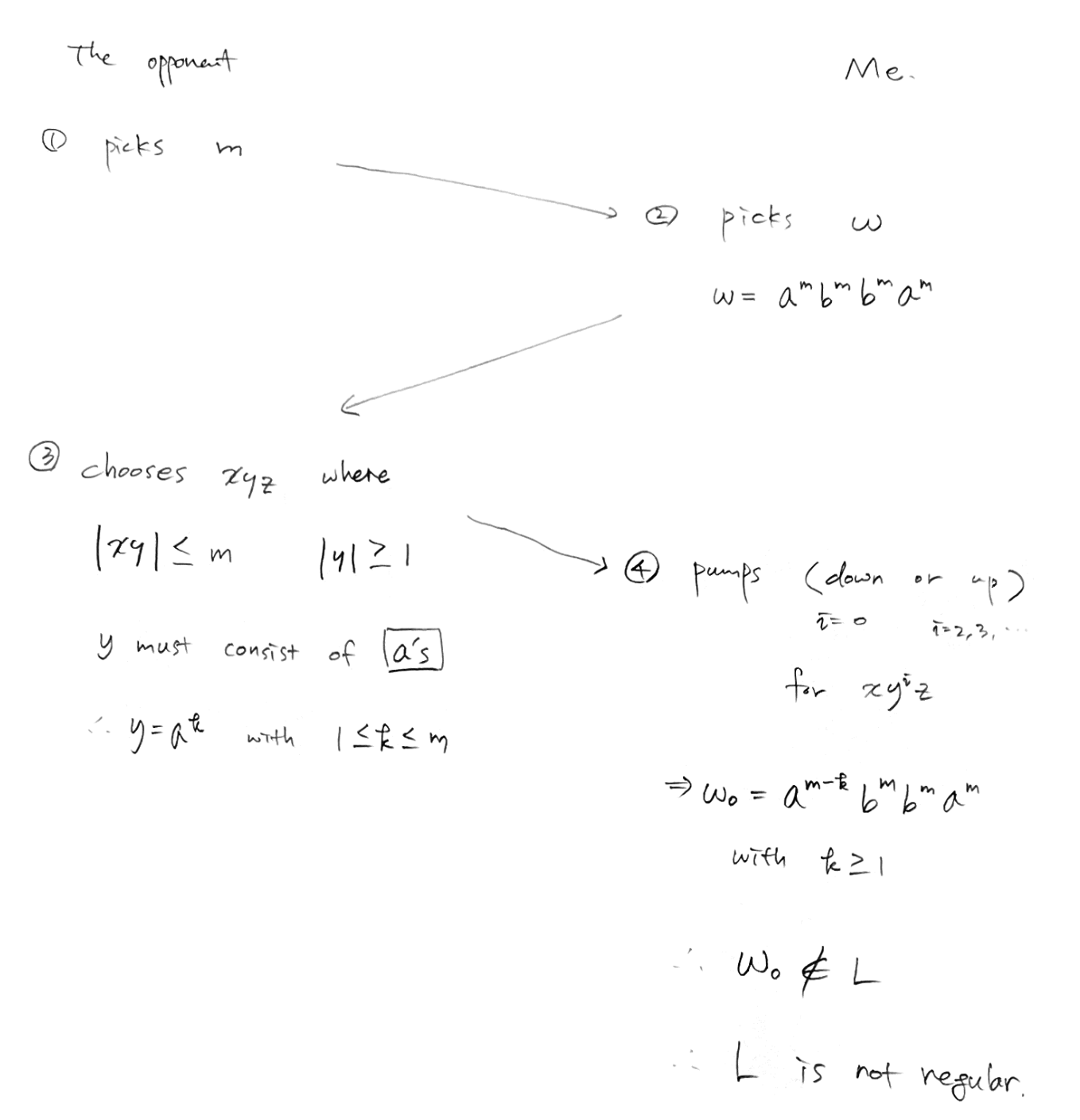
이번에도 대화하듯이 주고받는 형태로 증명을 해본다.
(기본 골자는 여전히 귀류법이다.)
1. 먼저 이 언어가 regular 하다고 믿는 상대방은 m 이라고 하는 길이를 제시한다.
2. 이 언어가 regular 하지 않다고 믿는 나는 더 긴 길이의 문자열을 제시한다.
이번에는 aᵐbᵐbᵐaᵐ 을 제시한다.
3. 상대방은 여기에서 |xy| <= m 이면서, |y| >= 1 을 만족하도록 하는 y 를 골라야 한다.
상대방은 y 로 aᵏ 을 선택할 수 밖에 없다. 하나의 상태에서 출발해서 같은 상태로 돌아오는 사이클을 찾는 다는 것은 정규표현식으로 * 를 찾는 것과 같은데, a라는 단일 문자를 선택할 수 밖에 없다. (만약 b를 고르면 b가 나오기 위해서는 m 개의 a가 나와야 하므로 조건을 m보다 길어져서 쓸 수 없다.)
4. 같은 과정으로 pumping down 을 해도, up을 해도 그 즉시 L에 속한 문장이 아니게 되므로 regular 하지 않다.

이번엔 이 예시를 다른 방법으로 풀어보자.
주어진 언어도 사실 regular 하지 않다. n, k 의 개수를 정확히 카운팅 해야만 c의 개수가 n+k 와 일치하도록 맞출 수 있는데, n, k 의 값이 무한하기 때문이다.
이 문제도 pumping lemma를 통해 non regular 하다고 판별할 수 있지만,
한번 지난 글에서 정리한 homomorphism 을 사용해서도 증명해볼 수 있다.
homomorphism 은 regular 언어에 대해서 닫혀있는 연산임을 기억하자.

만약 어떤 homomorphism 을 위와 같이 정의한다고 하면, 주어진 언어 L 을 aⁱcⁱ 형태로 나타낼 수 있다.
만약 L 이 regular 하다면 h(L) 역시 regular 한데, h(L) 이 나타내는 언어는 이미 regular 하지 않다고 했었던 형태이므로 모순이다.
따라서 L은 regular 하지 않다.

마지막으로 이 예시도 살펴보자.
n 과 k 의 개수가 다르다는 것 역시 매번 n, k의 개수를 카운팅 해야 하는데, 무한한 가짓수가 존재하므로 DFA, NFA로 나타낼 수 없다.
따라서 regular 하지 않다.
이 언어가 regular 하지 않다는 것은 기존에 알고있는 정리들을 기반으로 간단하게 증명할 수 있다.

만약 주어진 이 언어 L 이 regular 하다면, regular 언어는 여집합 연산에 대해서 닫혀있다.
주어진 언어를 단순히 여집합 취하면 aⁿbⁿ 이 되는 것이 아니다.
모든 a, b로 만들 수 있는 문장들 중에서 a 가 선행하고, b가 후행하면서 그 개수가 다른 것들을 제외한 문장들이 여집합 연산의 결과이다.
이 여집합 연산의 결과 역시 regular 하며, 이 결과에 대해 a가 선행하고 b가 후행하도록 제한을 걸은 L(a*b*) 언어를 교집합 연산을 취해준다. 이 언어는 regular 하므로 교집합 연산의 결과 역시 regular 하다.
그런데 이 교집합 연산의 결과는 우리가 봤었던 non regular 한 그 언어가 나온다.
따라서 처음에 regular 하다고 했던 가정이 모순이므로 L 은 non-regular 하다.
이렇게 regular language 에 대해 닫혀있는 연산을 활용해서도 non regular 를 증명할 수 있다.
'CS > 오토마타' 카테고리의 다른 글
| [오토마타] 13. Context-Free Language (0) | 2024.12.04 |
|---|---|
| [오토마타] 12. Toy Program for DFA (0) | 2024.12.04 |
| [오토마타] 10. Regular Language 의 Closure Properties (0) | 2024.10.24 |
| [오토마타] 9. Regular Grammar (0) | 2024.10.23 |
| [오토마타] 8. Regular Expression 과 Regular Language (0) | 2024.10.23 |
