지금까지는 어떻게하면 여러개의 DNA 시퀀스에서 공통된 motif 를 찾고, 찾아낸 motif 를 기존 DNA 에서 어떻게 표현할 것인지 (정렬할 것인지) 다양한 방법에 대해 정리하였다.
이번 글부터는 각각의 DNA 조각들을 모아서 하나의 게놈을 만드는 방법을 정리해본다.
아이디어

100권의 책을 파쇄한 뒤, 각 조각들을 잘 조립해서 하나의 페이지를 복원하려고 한다.

각 조각들을 올바르게 조립해서 하나의 페이지로 복원할 때, 각 조각에서 겹치는 부분들을 이용해서 페이지를 복원할 수 있다.
DNA 조각들을 모아서 하나의 게놈을 만들 때도 비슷한 방법을 사용하여 복원할 수 있다.
이때 이 방법을 위해서 그래프를 정의할 필요가 있다.
그래프는 read fragment 를 정점으로 하고, 두 fragment 사이에 얼마나 겹치는지 정도를 가중치로 갖는 간선을 갖는다.
이 그래프는 방향 그래프이며, 우리는 가능한 큰 가중치를 갖는 간선을 이용해서 모든 노드를 연결하길 원한다.
De Bruijin 이라는 네덜란드 수학자가 Minimal Superstring Problem 과, 이 문제를 풀기 위한 그래프를 제시했다.
이 문제는 Σ 를 알파벳으로 하는 길이가 k 인 모든 문자열을 포함하는 가장 짧은 문자열을 찾는 것이다.
예를 들어, { 0, 1 } 을 알파벳으로 하는 길이가 3인 모든 문자열을 포함하는 제일 짧은 길이의 문자열을 찾아보자.
먼저 가능한 길이가 3인 모든 문자열은 다음과 같다.
000
001
010
011
100
101
110
111
그리고 이 모든 문자열을 substring 으로 갖는 제일 길이가 짧은 문자열은 다음과 같다.

드 부루진은 이 문제를 그래프로 매핑해서 풀었다.

예를 들어 이 문자열의 5-mer 들을 모두 나열하면 11가지 종류가 존재한다.
(겹치는 5-mer 을 하이라이트로 표시함)
이때 5-mer 의 suffix인 (k-1)-mer 과 5-mer의 prefix 인 (k-1)-mer 이 같은 5-mer 사이에 간선이 존재한다고 보고 연결지을 수 있다.

이를 그래프로 나타내면 위와 같다.
이때 이 그래프를 보고 기존의 문자열을 어떻게 추론할 수 있을까?
해밀턴 회로
해밀턴 회로는 그래프의 모든 정점을 한번씩만 지나는 경로가 사이클을 이루는 것을 말한다.

우리가 찾으려는 경로는 위와 같이 찾을 수 있다.
이 경로를 찾는 프로그램을 어떻게 작성할 수 있을까?
또한 이 해답은 과연 유일할까?
먼저 해밀턴 경로에 대해서 '01' 을 알파벳으로 하는 길이가 4인 모든 문자열을 포함하는 Minimal Superstring Problem 을 풀어보자.
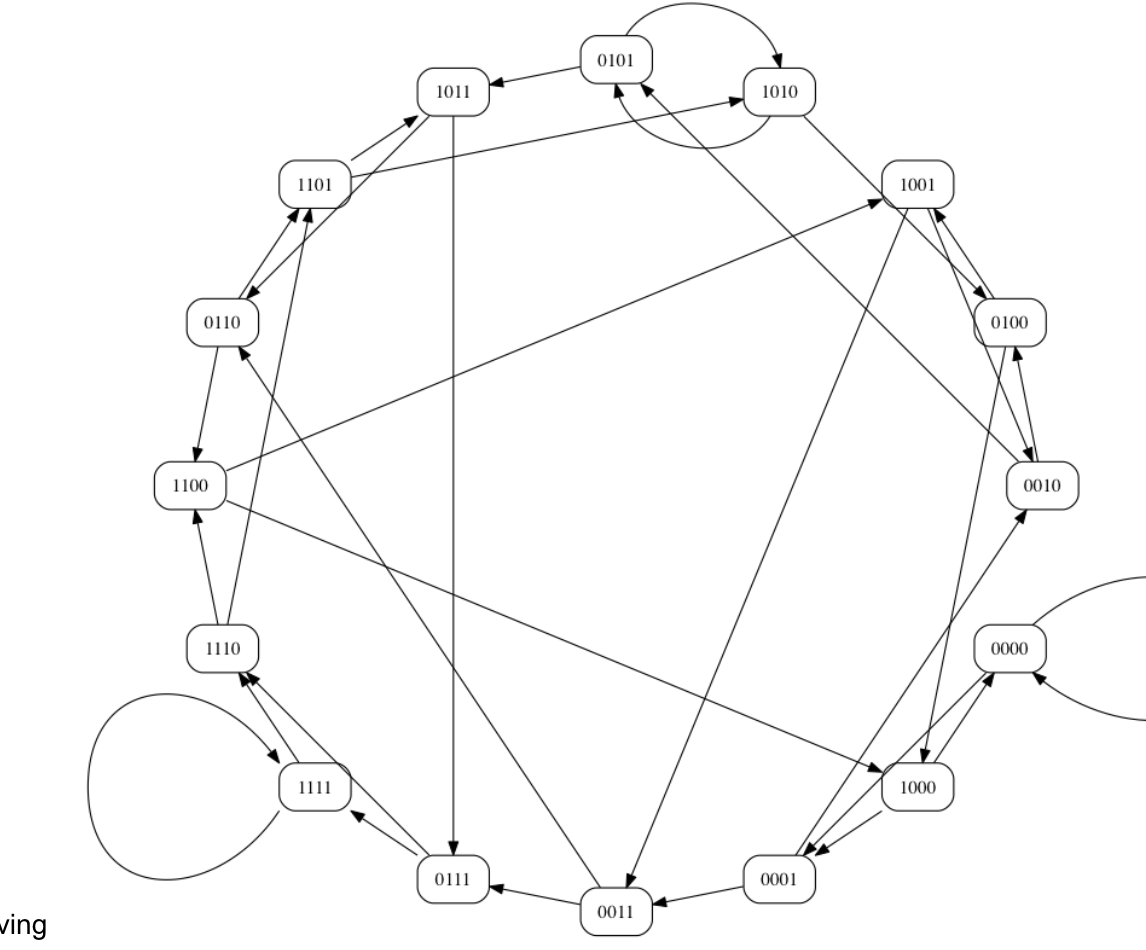
해밀턴 경로 방식에서는 이렇게 길이가 4인 문자열을 정점으로 하고, 길이가 3인 suffix 가 길이가 3인 prefix 와 겹치는 정점들에 대해 간선을 만든다.
이제 모든 간선을 한번씩만 방문하는 경로를 찾으면된다.
어떻게 찾을 수 있을까?
제일 간단한 방법은 각 정점들의 방문 순서에 대한 모든 순열을 다 시도해보는 것이다. (브루트포스)

정점 리스트에 대해 순열을 만들고, 모든 순열에 대해 이 순열이 가능한 순열인지 검증한다.
가능한 순열을 발견했다면 멈추고 해당 조합을 반환한다.
18분의 시간이 소요된 것을 알 수 있다.
해밀턴 경로에서는 정점에 대한 경로를 이어붙이면 super string 을 찾을 수 있다.
이때 첫 정점은 그대로 가져다 쓰고, 이후의 정점은 앞의 k-1 개는 제외하고 붙이면 된다. (k-1 개는 겹치므로)

이 방법은 하나의 경로를 발견한 즉시 멈추는 알고리즘이다.
그런데 같은 답을 내는 경로가 여러개 존재하지는 않을까?
드 브루진은 이 경로의 개수를 알아내는 공식도 만들었다.
σ = 알파벳을 구성하는 심볼의 개수 일 때, 위와 같은 공식이 성립한다.
만약 알파벳이 2개 원소로 구성되어 있고, 길이가 4인 모든 경우의 문자열을 포함하는 경로를 찾는다면 그 경로의 개수는 2! ** (2 ** (4-1) ) / 2**4 = 2 ** 8 / 2 ** 4 = 2 ** 4 = 16 개의 경로가 존재한다.
브루트포스는 너무 느리기 때문에 가자치기 테크닉을 이용해서 최적화를 할 수 있다.

경로를 구성할 때 순열을 다 만들어놓고 검증하는 것이 아니라, 순열을 직접 만들어보다가 중간에 안 만들어지면 멈추는 식으로 구성한다.
드 브루진 그래프와 오일러 경로
오일러 경로는 모든 정점을 1번씩 지나고, 그 과정에서 한번 지나간 엣지를 두번 이상 사용하지 않는 경로를 말한다.
드 브루진은 다음과 같이 그래프를 만들고 이 그래프에 대한 오일러 경로를 생각하여 문제를 푸는 방법을 제시했다.
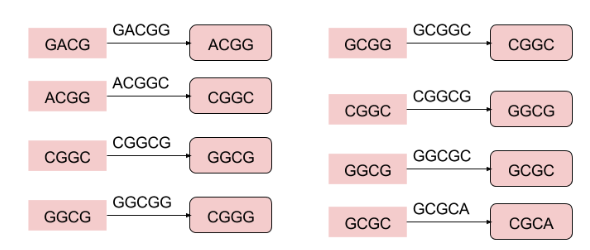
드 브루진은 k-mer 을 정점이 아니라 '간선' 으로 만드는 방법을 제시했다.
이떄 정점에는 그 k-mer 의 prefix 와, suffix 가 들어간다.

이를 그래프로 나타내면 위와 같은 그래프를 그릴 수 있다.
이 그래프에서 우리가 찾으려는 첫 문자열을 만드는 경로를 어떻게 찾을 수 있을까?

해밀턴 경로와 오일러 경로는 위와 같다.
이제 다시 원래 풀고자했던 문제로 돌아오면,
드 브루진의 Minimal Superstring Problem 문제는 k차원 드 부르진 그래프에서 해밀턴 경로를 찾으면 된다.
또는 k-1차원 드 브루진 그래프에서 오일러 사이클을 찾으면 된다.
드 브루진은 Minimal Superstring Problem 을 해밀턴 경로 문제 또는 오일러 경로 문제로 바꿀 수 있음을 알았다.
오일러 경로 찾기

1. 시작점에서 출발해 되돌아 올 때까지, 아직 방문하지 않은 간선을 따라 사이클을 찾는다.

2. 1, 2, 9 정점 중에 아직 사용하지 않은 간선이 존재하는 노드에 대해, 그 노드에서 출발하고 되돌아오는 사이클 경로를 찾는다.
2에서는 2 - 7 - 3 - 2 라는 사이클을 발견하였다.
이 경로를 기존에 발견한 경로와 합치면
1 - (2 - 7 - 3 - 2) - 9 - 1 이 된다.

3. 같은 과정을 반복한다.

4. 더 이상 사용가능한 간선이 없으면 멈춘다.

위와 같은 최종 경로를 갖게 된다.

오일러 경로 알고리즘 코드는 위와 같다.
반복문을 돌면서 만약 현재 간선의 시작점이 현재 정점이라면, 현재 정점을 도착점으로 바꾸고 방문한 간선을 제거한 뒤 break 로 for 문을 빠져나간다.
만약 for 문을 빠져나가지 않아서 현재 정점에서 방문 가능한 간선이 없다면 방문하지 않은 간선들을 돌면서 path 에 존재하는 정점들과 연결된 간선에 대해 같은 과정을 반복한다.
이 알고리즘이 동작해서 오일려 경로를 찾을 수 있으려면 다음 조건이 필요하다.
모든 정점에 대해 incoming edge, outgoing edge 수가 같은 그래프를 balanced graph 라고 한다.
1. 연결 그래프의 모든 정점이 balanced 한 것은 곧 오일러 사이클이 존재함을 의미한다. (필요충분조건)
2. 연결 그래프의 2개 정점이 semi-balanced 하고, 나머지가 모두 balananced 한 것은 곧 오일러 경로가 존재함을 의미한다. (필요충분조건)
semi-balance 는 incoming edge 와 outcoming edge 의 개수 차이가 1 인 것을 말한다.
이때 incoming edge 가 더 많은 정점이 경로의 끝, outgoing edge 가 더 많은 정점이 경로의 시작이 된다.
위 코드에서 VerifyAndGetStart() 메서드는 이 그래프가 오일러 경로 또는 사이클이 존재하는 그래프인지 검증한다.
만약 조건에 맞지 않다면 코드를 실행하지 않는다.

이를 기반으로 새로운 그래프 클래스를 작성할 수 있다.
한 가지 추가된 점은 eulerEdges 라는 메서드인데, 일반적인 오일러 경로 알고리즘은 '정점의 순서' 를 찾지만, 우리가 그래프를 구성할 때는 k-mer 를 간선에 넣었기 때문에 간선들의 순서가 더 중요하다. 따라서 그 간선의 순서를 출력하는 별도의 메서드를 만들었다.

이 그래프를 사용하여 기존의 Minimal Superstring Problem 을 풀어보면 위와 같이 풀 수 있다.
0, 1 을 알파벳으로 하는 길이가 4인 모든 문자열에 리스트(binary)가 있을 때, 이 모든 문자열을 포함하는 최소 길이 문자열을 찾아보자.
오일러 경로 알고리즘을 사용한다면 node 는 각각의 앞 3개, 뒤 3개 prefix, suffix 가 정점이 된다.
중복을 제거한 각 정점들에 대해 그래프를 구성한다.
간선의 경우, 길이가 4인 문자열을 weight 로 하는 간선을 추가한다.
오일러 경로 알고리즘을 통해 찾은 path 를 구하고, 이 path 를 간선들의 path 로 변형한 뒤 (edges), 이 간선들을 하나의 문자열로 합친다.
이때 첫 edge는 그대로 가지고 오고, 그 뒤에서부터는 맨 뒤 글자만 가져온다. (앞의 k-1 개 문자는 겹치므로)

실행 결과는 위와 같다.

이를 그림으로 나타내면 위와 같이 나타낼 수 있다.
이 그래프에 대해서 오일러 경로를 찾는 것과 같다.
시작점은 임의로 000 에서 시작하도록 잡았다.

그러면 위와 같이 경로를 찾는다.
Assembling Genome
알고리즘 설명이 매우 길었다.
다시 기존의 목표인 DNA 시퀀스 조각들을 모아서 하나의 게놈을 만드는 방법을 알아보자.
Minimal Superstring Problem 에서는 모든 k-mer 를 포함하는 superstring 을 찾는 것이 목표였다.
그리고 경로는 여러가지가 있을 수 있었으며, 이 모든 경로가 해답으로 가능했다.
하지만 read fragment 들을 모았을 때 이들은 모든 k-mer 를 포함한다고 단정지을 수 없다.
또 휴리스틱을 사용하지 않는 한 반복적으로 등장하는 k-mer을 명확하게 조립할 수 없다.

길이가 20인 시퀀스를 5-mer 로 분할하면 위와 같다.
이 5-mer 들을 조립해서 다시 기존의 시퀀스를 복원할 수 있을까?
우선 각 5-mer 중에서 반복되는 5-mer 들을 구분하기 위해 다음과 같이 구분자를 붙여주었다.

그리고 위에서 작성한 해밀턴 경로 함수를 적용하여 minimal superstring problem 을 푸는 것과 동일하게 접근하였다.

하지만 결과가 조금 다르게 나온다.

우리가 기대한 경로는 왼쪽 경로인데, 실제로는 오른쪽 경로를 만들어낸 것을 볼 수 있다.
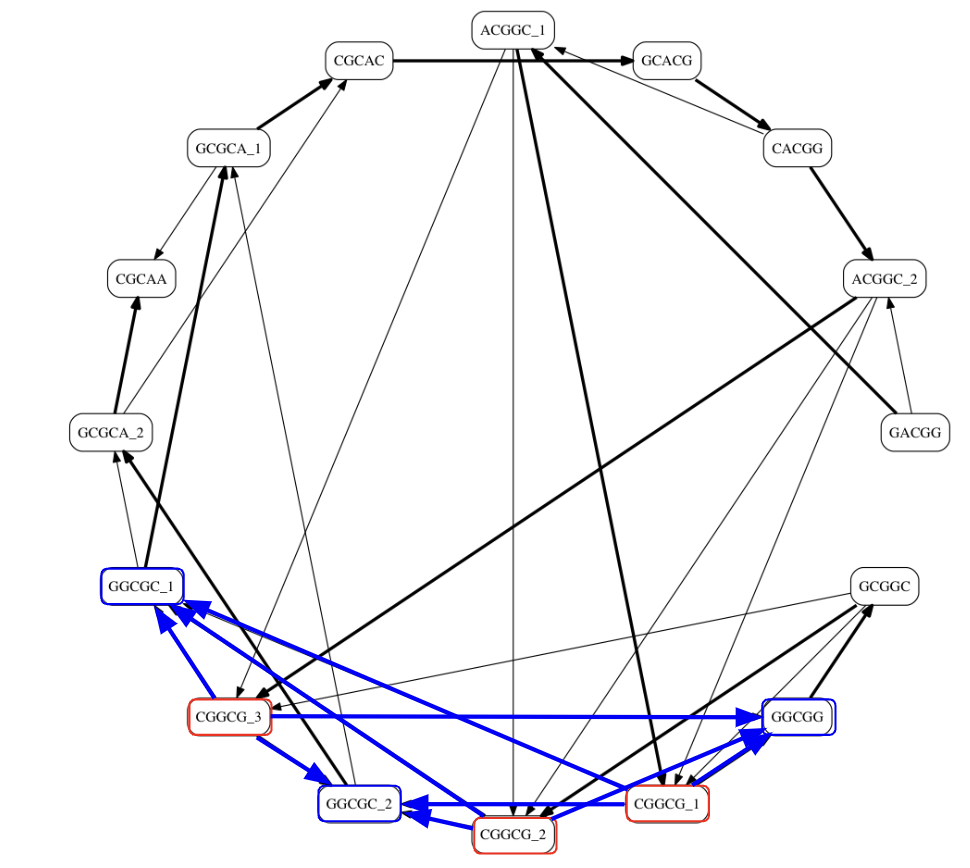
문제는 여기에서 발생한다.
CGGCG 라는 정점이 3개가 있고, 각 정점에 대해 GGCGC 로 가는 경우와 GGCGG 로 가는 경우 2개로 나누어진다.
그러면 해밀턴 경로 말고 오일러 경로 방식으로 문제를 풀어보면 어떨까?
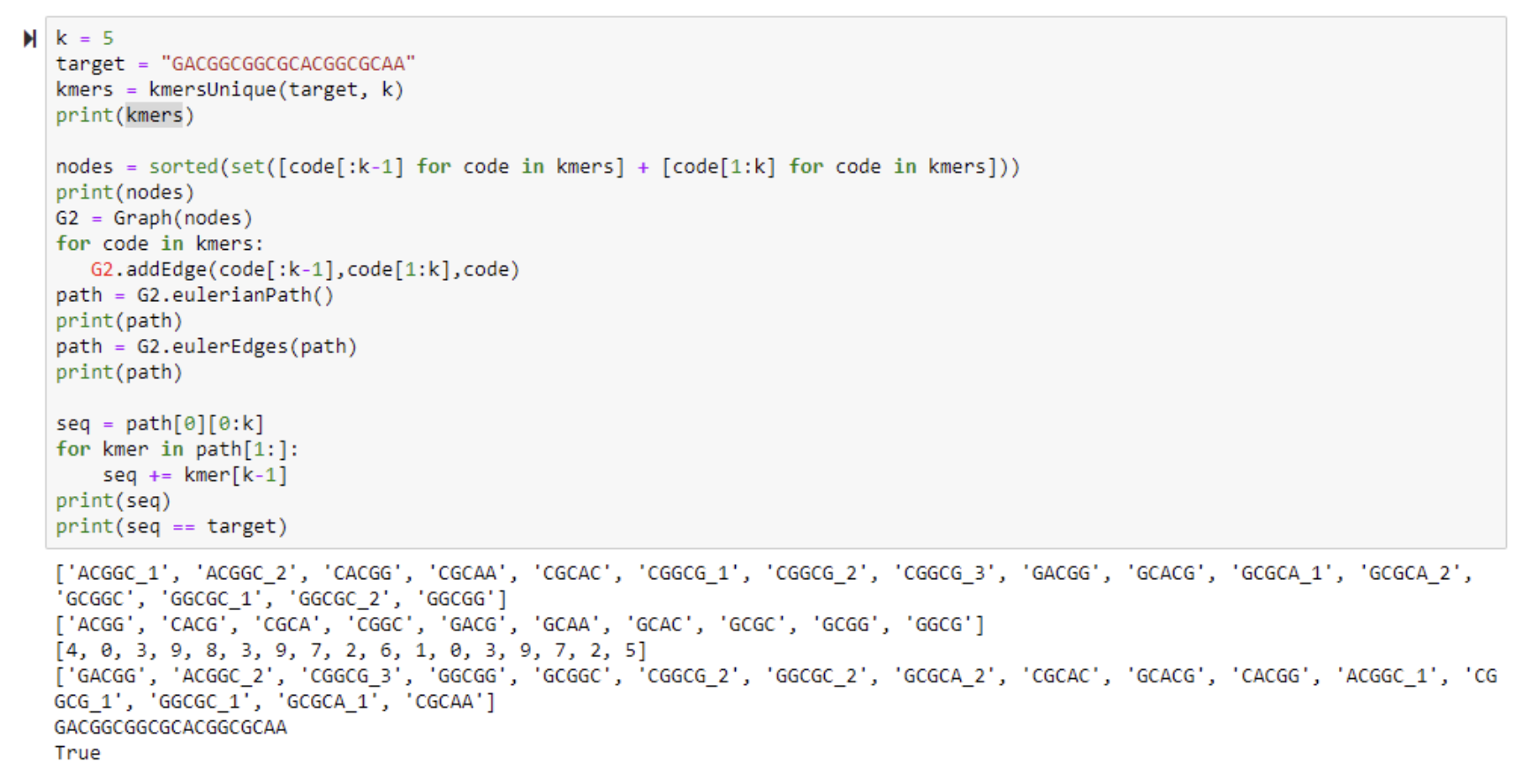
오일러 경로 방식은 한번에 문제를 풀었다!
하지만 이건 운이 좋았을 뿐, 해밀턴 경로 방식으로 풀었던 경로 역시 오일러 경로에도 똑같이 존재한다.

어떤 사이클을 먼저 도는지에 따라 결과가 달라진다.
이 문제를 해결하기 위해 k-mer 의 k 를 더 키우는 방법이 있다.

기존의 k = 5 와 마찬가지로 k = 8 로 키웠을 때 정답을 똑같이 구한다.
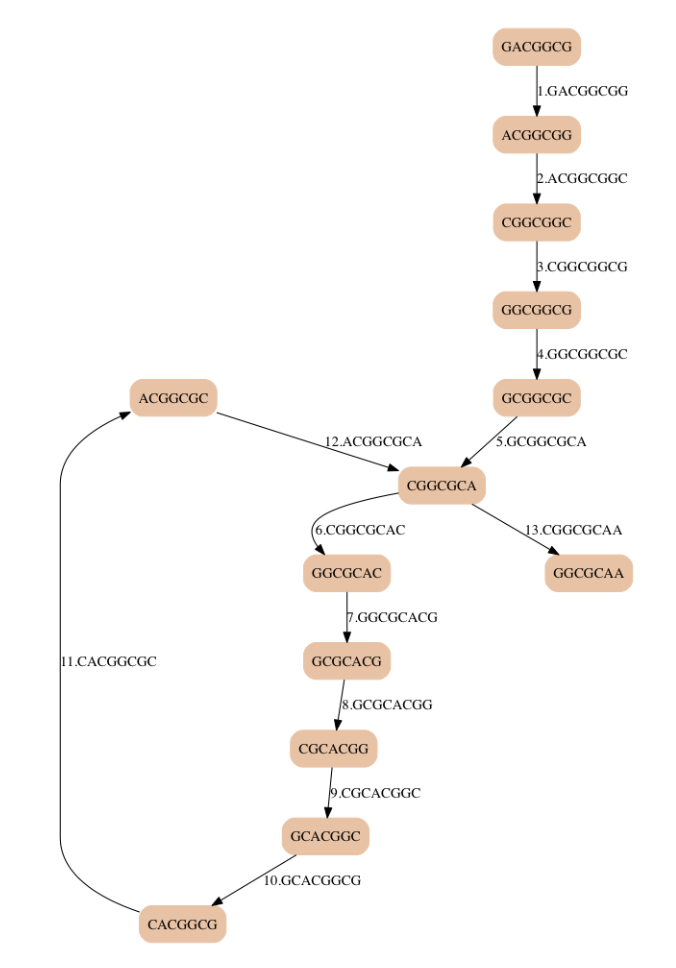
이렇게 k 를 키우면 앞서 봤던 사이클이 여러개 등장해서 잘 선택해야 하는 문제가 사라진다.
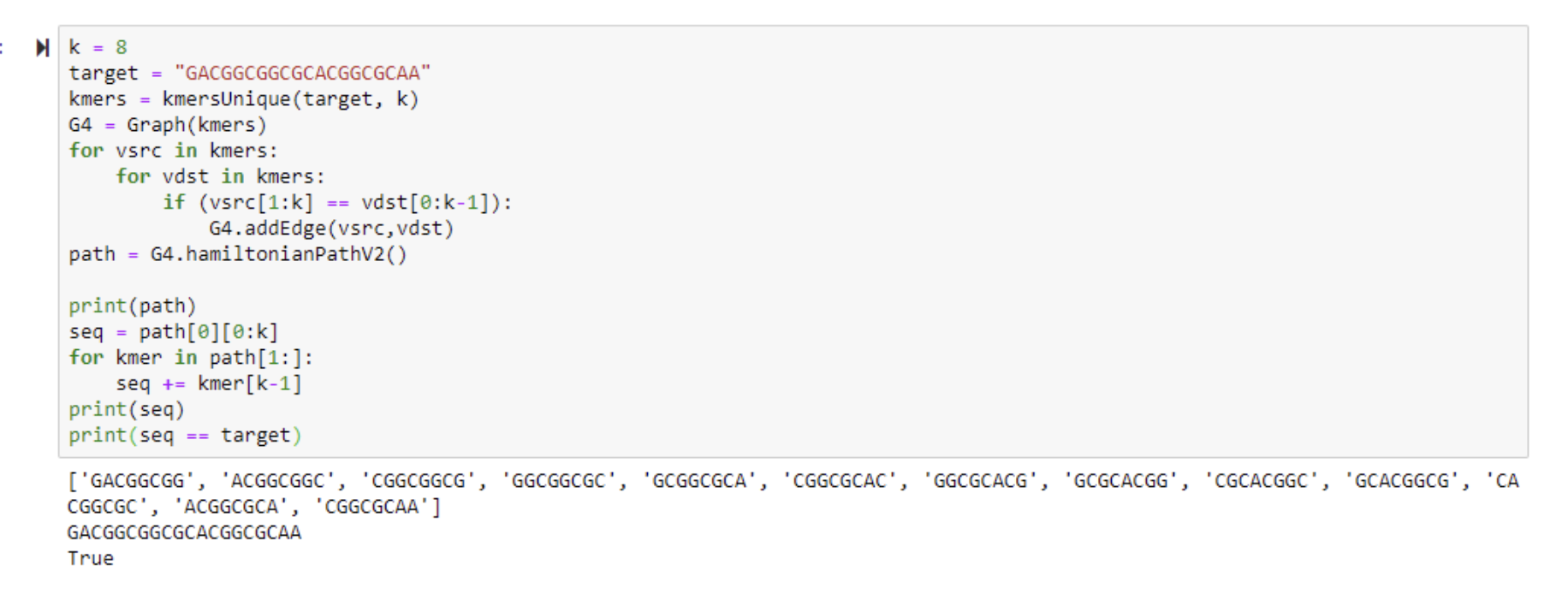
k 를 키우는 방법은 해밀턴 경로를 사용한 해결책에서도 유효하게 작동한다.
하지만 같은 k-mer 이 여러번 중복해서 등장하는 문제는 여전히 남아있다.
같은 k-mer 을 구별할 수 없다면 중복을 제거하고 unique 한 k-mer 에 대해서 경로를 찾으면 어떨까?

unique 한 5-mer 을 가지고 k-1 차원 드 브루진 그래프를 만들었더니 위와 같이 나왔으며 오일러 경로가 존재하지 않았다.

이때 여기에서 녹색, 빨간색, 파란색, 노란색, 보라색 경로를 따라가면 어떤 시퀀스를 만들 수 있다.
이 시퀀스를 가리켜 contig 라고 부른다.
이 시퀀스는 out-degree > in-degree 인 노드를 만날 때까지 특정 지점에서 시작해서 쭉쭉 따라가면 만들어진다.
예를 들어 파란색 경로의 경우, out-degree = 1, in-degree = 1 인 상태에서 쭉 가다가 in-degree = 1, out-degree = 2 가 되었을 때 멈추고, 그 분기점에서 각각에 대해 새로운 contig 를 만들어 노란색과 보라색 contig 를 시작한다.

이제 이 contig 들을 가지고 그래프를 만든다.
이때 각 엣지의 weight 는 얼마나 중첩되는지를 나타낸다. (suffix와 prefix 가 겹치는 최대 길이)
이 그래프는 보통 k-mer 로만드는 그래프보다 훨씬 작은 사이즈로 만들어진다.
여기에 가끔 드 브루진 그래프에서 나왔던 아이디어를 적용하여 추가적인 엣지를 넣기도 한다. (?)

이 그래프에 대해 가장 무거운 (가중치 합이 큰) 경로를 찾으면 그 문자열이 우리가 찾는 문자열이다.
'CS > 문제해결기법' 카테고리의 다른 글
| 9. 문자열 패턴 찾기 (6) | 2024.12.11 |
|---|---|
| 8. 단백질 서열 결정 (4) | 2024.12.10 |
| 6. Advanced Sequence Alignment (0) | 2024.10.29 |
| 5. Aligning Sequences (0) | 2024.10.29 |
| 4. Finding TFBS Motifs in our lifetime (0) | 2024.10.29 |
