DNA로 돌아와서, 자주 반복되는 DNA motif 를 찾거나, 가장 자주 등장하는 k-mer를 찾거나, 특정한 k-mer가 얼마나 자주 등장하는지 알고 싶을 때 문자열 패턴 매칭 알고리즘을 사용할 수 있다.
제일 근본적인 패턴 매칭 문제는 문자열에 특정 패턴이 존재하는지 확인하고, 존재한다면 그 위치는 어디인지 찾는 것
제일 나이브한 방법은 문자열을 직접 순회하면서 찾는 것이다.
이때는 패턴의 길이가 n이고, 문자열의 길이가 m일 때, O(mn) 의 시간이 걸린다.

근데 이걸 조금 더 최적화 해보면,
위와 같은 문자열에서 ssi 를 찾는다고 할 때, SS까지 일치했는데, i가 m이랑 불일치해서 실패한 경우,
우리는 그 다음에 시도할 위치를 한번 건너뛸 수 있다.
우리가 찾는 패턴의 prefix ss가 지금 보고 있는 suffix 'sm' 과 다르기 때문이다.
이 방법을 통해 O(n)에 가깝게? 줄일 수 있는 것 같은데,
그럼에도 패턴의 개수가 늘어나면 시간이 오래 걸린다.
이때 우리가 시도할 패턴 문자열들을 전처리해서 비교 횟수를 줄이는 방법을 고안할 수 있다.
Trie

그 방법 중 하나는 위와 같은 keyword tree 를 만드는 것.
같은 prefix를 공유하는 패턴들을 합쳐서 트리로 표현하는 것
엣지에 심볼을 적는다.
이와 관련하여 Trie 구조도 있다.
Trie는 시퀀스와 관련된 트리로, 보통 트라이의 노드/엣지는 시퀀스의 심볼과 1대1로 일치한다.
(위 그림에서 보는 게 트라이 인 것 같다.)
그렇다면 Prefix Trie 매칭을 해보면,
위 트리에 apple 을 넣어보면 노드를 따라가서 빨간색 노드 (끝 점) 에 도달할 수 있으니 일치하는 문장
band 를 넣으면 들어가지기는 하나 중간에 멈추고 빨간색에는 도달하지 못하니 일치하지 않는 문장
april 을 넣으면 l 에서 더이상 이동 가능한 간선이 없으므로 일치하지 않는 문장임을 판별할 수 있다.
성능은 O(nm) 이때 n은 탐색할 문자열의 길이, m은 트리에 존재하는 패턴 중 제일 긴 길이이다.

이런 식으로 구현할 수 있다.
여기에서 $ 기호는 이게 문장의 끝임을 나타낸다.

여기에 더해 이렇게 failure edge를 추가해서 트라이를 더 개선할 수 도 있다.
예를들면 banda 까지 시도했다가 뒤에 n이 안나와서 실패했다면, 그 다음에는 이 마지막 a에서 시작하는 apple을 시도해볼 수 있도록 바로 p로 넘어갈 수 있는 정점과 연결하는 것이다.
Suffix Trie
하지만 그럼에도 이 방식은 여러개의 패턴을 동시에 매칭하고자 할 때 성능이 좋지 않다.(?)
그래서 패턴의 prefix 를 저장하는 구조 말고, 주어진 text의 모든 suffix를 저장하는 구조를 만들면 어떨까 하는 아이디어가 나왔다.
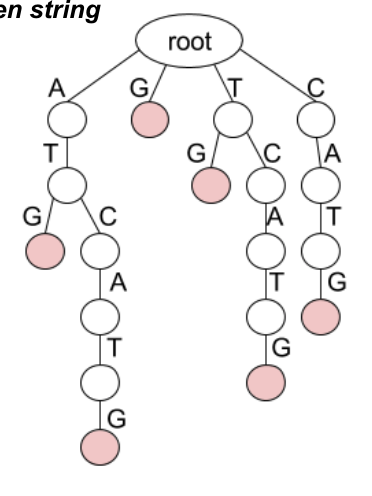
그래서 등장한 Suffix Trie
이 suffix text 안에 CAT 이 있는지는 어떻게 찾을 수 있을까?
간단하다. 기존에 패턴으로 만든 prefix trie에서 하듯 CAT을 여기 트라이에 넣어보면 된다.
그러면 빨간색 노드에는 닿지 못하지만 CAT이 존재한다는 것을 알 수 있다.
(우리가 찾으려는 패턴이 suffix들 중 일부의 prefix 이기 때문이다).
이러한 suffix tree 는 이렇게 압축도 할 수 있다.

리프노드에는 suffix 인덱스를 기술한다고 한다.

이런 suffix tree는 문자열의 길이가 m 일 때 O(m) 시간에 만들 수 있다.
그리고 패턴을 찾을 때는 패턴의 길이가 n 일 때, O(m + n) 시간에 찾을 수 있다.
(오....)
여러개의 패턴을 찾을 때는 그 개수가 k 일 때, O(m + kn) 에 찾을 수 있다.
(오.......)
대신 suffix tree 의 단점은 메모리 오버헤드가 크다는 것.
(문자열의 모든 suffix를 저장해야 하는데, 보통 문자열은 매우 기니까..)

이런 suffix tree 가 있다고 할 때, 다음과 같은 문제를 풀 수 있다.
1. 이 suffix tree가 나타내는 문자열은 뭘까? -> 리프노드가 1인 쪽에 해당하는 문자열을 읽으면 된다. ATGCATACATGG
2. 어떤 문자가 가장 자주 나타날까? -> 루트에서 시작하는 간선 각각에 대해 제일 많은 리프노드를 가진 애를 찾으면 된다.
3. ATG는 얼마나 많이 나타났을까? -> ATG까지 타고 들어간 뒤, 그 서브트리의 리프노드 개수를 세면 된다. 2개
4. 가장 긴 반복되는 k-mer의 길이는 몇일까? -> 리프노드가 2개 이상인 제일 긴 path를 찾으면 된다. ATG, CAT 인 거 같다.
Suffix Array
suffix tree는 저장 공간을 많이 차지하는 문제가 있다.
저장 공간을 덜 잡아먹는 다른 자료구조는 없을까?
일단 먼저 생각할 수 있는 건, suffix 가 쭉 있을 때, 여기에서 패턴매칭을 하려면 모든 suffix를 훑어야 한다.
이건 별로 시간복잡도가 안좋으니 suffix를 미리 정렬해두고 이분탐색으로 찾는 방법을 생각할 수 있다.

이렇게 suffix가 정렬된 리스트가 있다고 할 때, 다음과 같은 질문을 해결할 수 있다.
- nana가 등장하는가? : nanas 를 이분탐색으로 찾아가면 찾을 수 있다.
- ana가 몇번 등장하는가? : ana를 prefix로 갖는 것들을 찾으면 된다. 3개 등장
- 가장 많이/적게 등장하는 문자 : suffix 문자열들의 맨 앞 문자로 통계를 내면 된다.
- 가장 많이/적게 등장하는 2글자 문자열 : suffix 문자열들의 2글자 prefix를 보면 된다.
suffix array는 크기가 O(m²) 이므로, 정렬비용은 O(m²log(m)) 이다.
suffix array를 정렬할 때 직접 문자열을 다 넣고 정렬할 수도 있겠지만, 효율적으로 정렬하기 위해서 인덱스 기반으로 정렬할 수도 있다.
이를 args sort 라고 한다.
즉, 초기의 위치에 대해 인덱스를 매긴 뒤, 이 인덱스값을 토대로 정렬된 리스트를 표현하는 것이다.

첫 번째와 같은 리스트가 있을 때, 이걸 생으로 정렬한게 두 번째 리스트
세 번째 리스트는 두 번째 리스트와 같은 정렬 결과를 인덱스로 표현한 것이다.
9가 맨 처음에 있는데, 기존 배열에서 9의 인덱스는 6이었으므로, 정렬된 데이터를 인덱스를 타고 들어가서 찾을 수 있다.

이렇게 정렬할 수 있다고 한다.
근데 사실 suffix array를 나타낼 때는 이 방식을 쓰면 input string 만 가지고 input string 에서 offset을 찍어서 suffix를 표현할 수 있다.
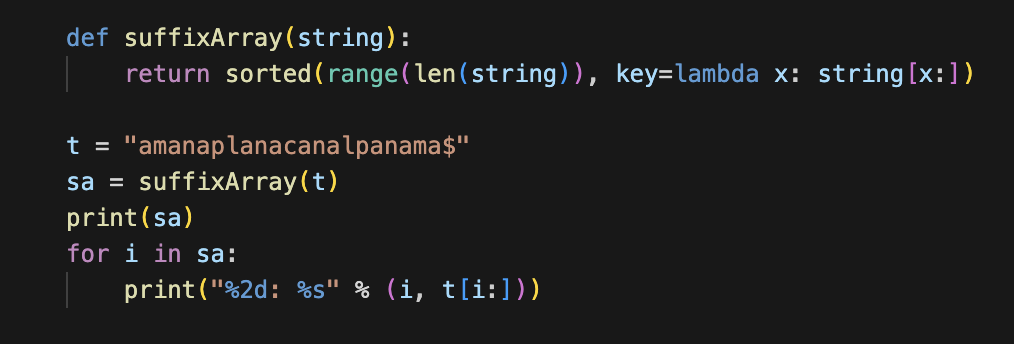
최종 suffix array 를 이렇게 만들 수 있다.
결국 이걸 만든 건 위에서 봤다시피 패턴 매칭을 하기 위해서다.
한번 패턴 매칭도 해보자.

이진탐색을 통해서 suffix array에서 처음으로 매칭되는 위치를 찾을 수 있고,

조건만 조금 틀면 제일 마지막으로 매칭되는 위치 역시 찾을 수 있으므로, 매칭 문자열이 나타나는 범위를 특정해서 '몇 개가 매칭되는지' 도 알 수 있다. (오....)
LCP
suffix array로 부터 LCP (Longest Common Prefix) 라는 보조 데이터를 계산할 수 있다.

이건 suffix array가 이렇게 정렬되어서 존재할 때, 바로 직전 문자열과 비교해서 prefix 가 얼마나 겹치는지 그 길이를 나타낸다.
이를 이용하면 아래와 같은 질문에 쉽게 답할 수 있다.
1. 가장 길게 반복되는 k-mer 는 무엇인가? : 제일 큰 숫자를 찾으면 된다. 숫자가 0이 아니라는 것은 이전 문자열과 현재 문자열 모두 등장했다는 뜻이니 최소한 1번은 반복적으로 나타난 k-mer 이다.
2. 몇개 종류의 문자가 등장했는가? : 0이 되엇다는 것은 아예 새로운 문자가 등장했다는 뜻이니 0의 개수를 세면 된다.
BWT
BWT는 suffix array와 같은 효과를 얻을 수 있으면서 텍스트 압축까지 가능하다.
먼저 기존 텍스트 뒤에 $ 표식을 추가하고 BWT 로 변환하면

이렇게 바뀌는데, BWT는 여러 문자들이 반복적으로 등장해서 이를

이런 식으로 압축할 수 있다.

BWT는 텍스트 뒤에 $를 추가하고 한 칸씩 로테이션한다.
그리고 그 텍스트 리스트를 정렬한 뒤 맨 뒤에 있는 문자를 세로로 읽은 것이 BWT 이다.
이때 $ 기호가 문자열의 끝을 나타내기 때문에, 텍스트 리스트를 정렬하고 보면, $ 기호 앞을 보면 suffix array와 똑같다.
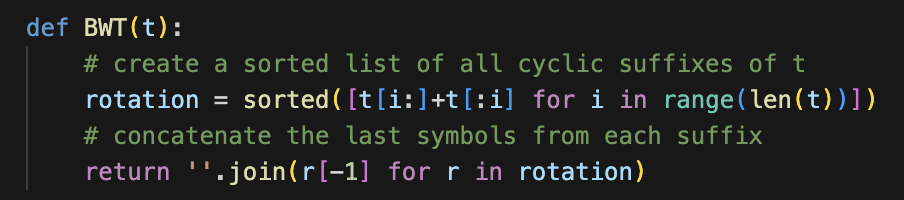
파이썬으로는 이렇게 구할 수 있다.
위에서 말한 것처럼 BWT는 suffix array와 공통점이 있기 때문에, 기존의 suffix array로부터도 BWT를 만들 수 있다.
BWT를 이루는 문자들의 공통점은, 그 문자들이 suffix 의 바로 직전 문자라는 점을 이용한 것이다.

그러면 이렇게 구할 수 있다.
BWT로부터 기존의 문자열을 복구하는 것 또한 어렵지 않다.

매 라운드마다 BWT 문자열을 앞에 추가하고, 문자열을 정렬하는 것을 BWT 길이만큼 반복하면 된다.
(0 ~ 7 까지 단계에서 맨 왼쪽에 있는 문자를 세로로 읽어보면 매 단계 항상 BWT를 앞에 붙여주고 있음을 알 수 있다.)
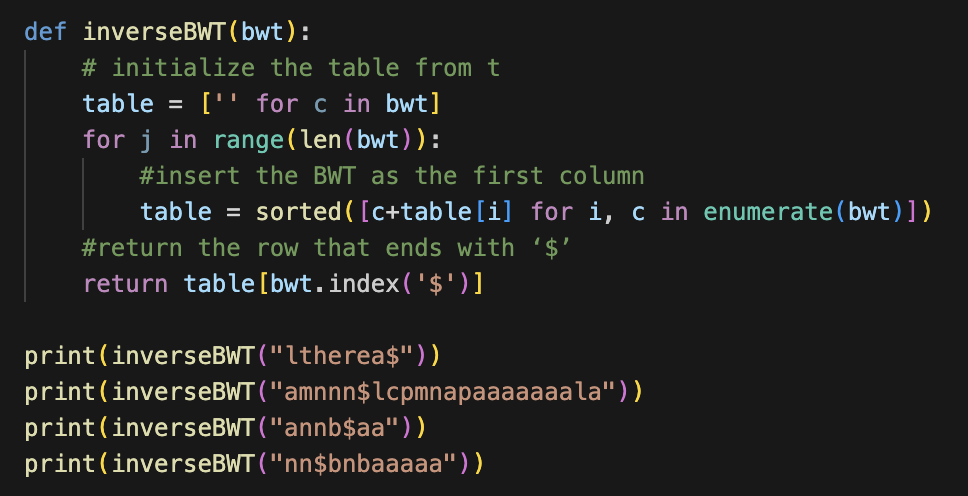
그래서 이렇게 bwt로부터 bwt를 만들었던 원본 문자열을 어렵지 않게 복원할 수 있다.
또한 이를 이용하면 BWT로부터 역으로 suffix array를 만들어 낼 수도 있다.
그렇다면 BWT는 간접적으로 suffix array의 성질을 내포하고 있다는 것과 같은데,
이를 이용해서 패턴 매칭에 활용할 수는 없을까?
BWT를 이용한 패턴 매칭

BWT를 만들 때 봤던 이 그림을 보면 그 성질을 알 수 있다.
BWT는 suffix array의 직전 문자로서, suffix array의 상대적인 순서를 보존하고 있다.
예를 들어, bwt에서 첫번째로 등장한 a는 suffix array에서 첫번째로 등장한 a 이며, 기존 문자에서는 뒤에서부터 세었을 때 첫 번째로 등장한 a이다.
그 다음에 bwt 에서 첫 번째로 등장한 n은 suffix array에서 첫번째로 등장한 n 이며, 기존 문자에서는 뒤에서부터 세었을 때 첫 번째로 등장한 n이다.
이렇게 같은 문자 사이에서 상대적인 순서를 보존하고 있는 것이다.
그리고 또 한가지 재미있는 점은 bwt를 사용하면 suffix array를 순회할 수 있다.
bwt 에서 첫 번째 문자 a는 suffix array에서 첫 번째로 등장한 a이다.
suffix array에서 해당 a를 찾고, 그 suffix array의 직전문자 (사실상 위 표현을 보면 맨 뒤의 문자를 읽어보면 된다.) 를 확인하면, 첫 번째 n이 나오며, 첫 번째 n의 직전 문자는 bwt로 확인할 수 있다.
따라서 이 과정을 반복하면 suffix 를 기존 문자열에서 존재했던 순서대로 순회할 수 있다.
이를 가리켜 First-Last mapping property 라고 표현한다.
FM Index
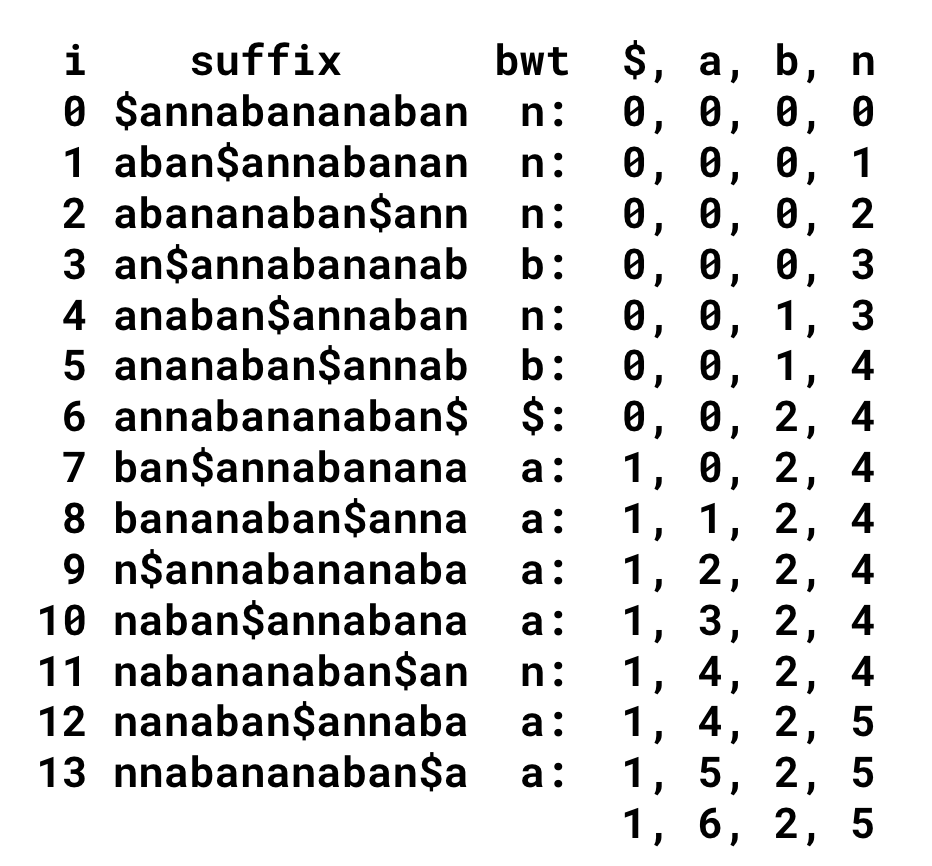
Fisrt-Last mapping 은 FM Index 를 통해 구현할 수 있다.
FM Index 는 해당 bwt의 문자가 suffix array 에서 해당 문자의 첫 등장위치로부터 얼마나 떨어진 곳에 존재해야 하는지 offset 을 순차적으로 기록한 것이다.
예를 들어 i = 5 행을 읽어보면 bwt[5] = b 이다. 이때의 FM index 데이터를 살펴보면 이 이전에 b가 1번 등장했고, n은 4번 등장했다 라는 것을 알 수 있다.
FM index 는 LCP 처럼 보조적인 용도로 사용할 수 있는 데이터 구조이다.

이렇게 생성한다.
FM index 를 사용하면 특정 suffix 의 바로 직전 suffix를 O(1)에 알아낼 수 있다.


이 성질을 이용해 이렇게 suffix 를 순차적으로 복원할 수 있다.
그리고 FM Index를 활용하면 드디어 BWT로 패턴 매칭을 할 수 있다.
패턴 매칭은 패턴을 거꾸로 순회하면서 찾는다.
nana 라는 문자열을 매칭한다면 a - n - a- n 순서로 매칭해나간다.

이 과정을 통해 매칭된 문자가 존재하는 범위를 바로 계산할 수 있다.

구현 결과는 위와 같다.
하지만 단점은 BWT 자체는 작지만, FM index의 사이즈가 커질 수 있다는 단점이 있다.
FM index 의 크기는 '사용된 문자 심볼의 가짓수 x BWT 길이'이기 때문이다.
MS BWT
multi string BWT
말 그대로, 여러 개의 문자열에 대한 BWT를 한번에 모아놓는 것을 말한다.

2개 문자열의 BWT를 만드는 과정이 이렇게 있을 때 합쳐서 정렬하여 MSBWT를 만들 수 있다.

심지어 FM Index도 이렇게 섞인 형태에 대해서 같이 가져갈 수 있다.
그리고 사용법도 기존의 BWT와 동일하게 사용할 수 있다.
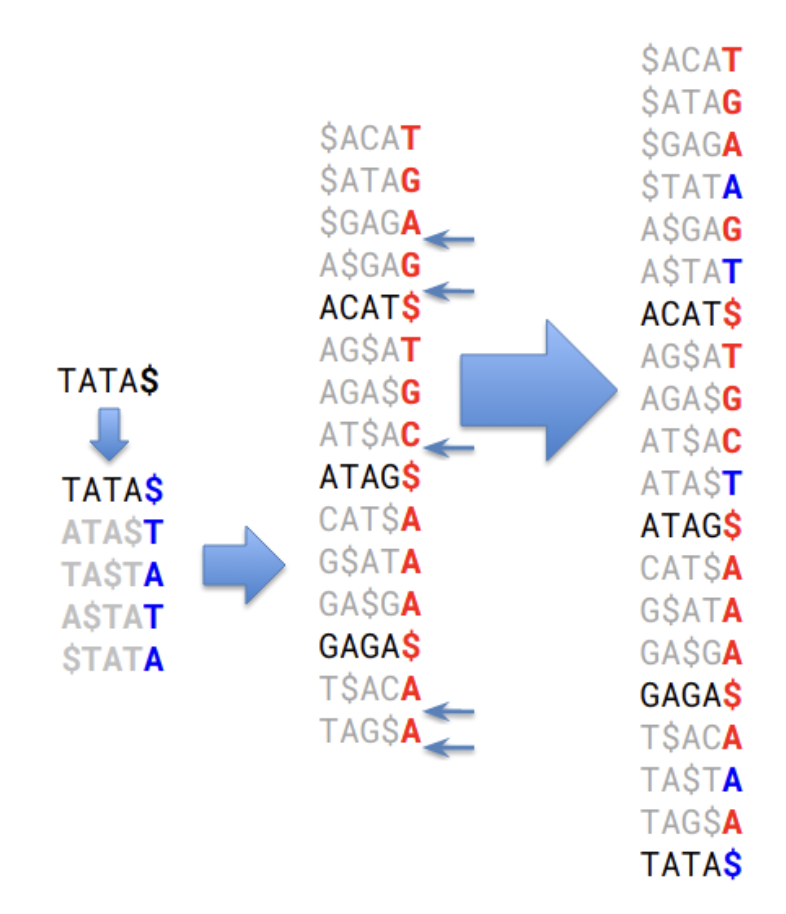
이렇게 정렬을 유지하도록 끼워넣어서 기존의 MSBWT에 새로운 BWT를 삽입할 수도 있다.
(근데 성능은 좋지 않다.)

MS BWT로부터 위와 같은 질문에 답할 수 있다.
1. msBWT에 몇 개 문자열에 대한 BWT가 있는가? => $ 개수를 세면 되므로 3개 문자열이 존재한다.
2. 각 문자열은 무엇인가? => 맨 처음 3개 줄을 읽으면 된다. ACAT, ATAG, GAGA 이다.
3. 어떻게 이것을 msBWT 문자열만 가지고 알아냈는가? => 음...?

BWT 하나를 msBWT에 삽입하는 건 비용이 존재하지만,
msBWT 2개를 하나로 합치는 건 비교적 간단하다.

병합 알고리즘은 다음과 같다.
먼저 msBWT 2개를 이렇게 두고, 그 옆에는 두 msBWT를 합쳐서 정렬한 결과를 쓴다.
(병합 알고리즘은 이해를 못함...)
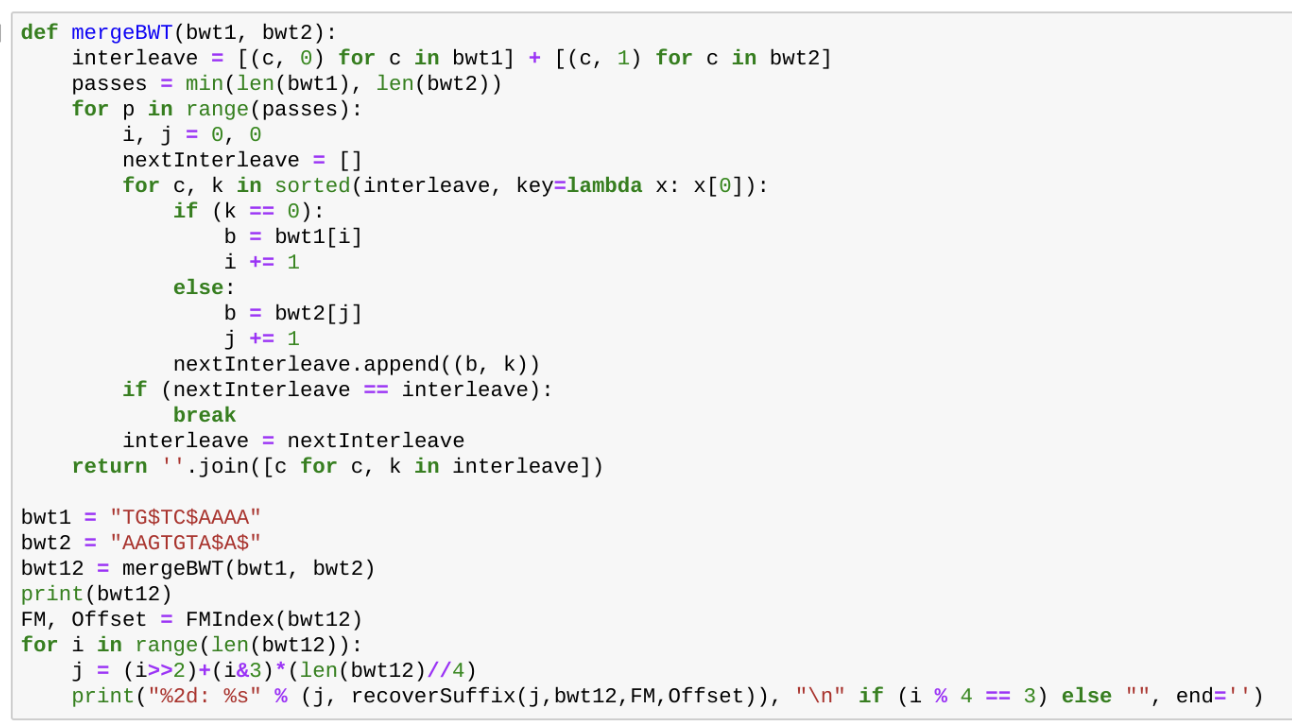
파이썬 코드는 요래 쓸 수 있다더라..
msBWT는 여러 문자열에 대해 동시에 패턴 매칭이 되니 성능이 좋다고 하는 것 같다.
유전자 분석에 유용한 듯..
'CS > 문제해결기법' 카테고리의 다른 글
| 11. Hidden Markov Models (카지노 동전 문제) (1) | 2024.12.11 |
|---|---|
| 10. 게놈 재배치 (팬케이크 뒤집기 문제) (0) | 2024.12.11 |
| 8. 단백질 서열 결정 (4) | 2024.12.10 |
| 7. Assembling a Genome (0) | 2024.10.30 |
| 6. Advanced Sequence Alignment (0) | 2024.10.29 |
