(문해기는 시간이 없어서 간결하게 정리할 예정..)
지금까지는 DNA에 대한 이야기였다면 이번에는 단백질에 대한 이야기를 해보자.
단백질은 아미노산들의 조합으로 구성된다.
각각의 아미노산은 탈수결합을 통해 합쳐지며, 그 결과물을 residue 라고 부른다.
이때 20가지 아미노산 residue 의 분자량은 이미 정확하게 잘 알려져 있다.
PIT 라는 고분자에 대해, PIT, PTI, ITP 등 순서는 분자량에 영향을 주지 않는다.
따라서 이들 각각을 2개로 쪼갰을 때, (PI, IT) 와 (PT, TI) 의 분자량 합은 같다 (?)
20가지 아미노산에 대해 결합에 참여했을 때 물이 빠진 상태의 분자량을 하나의 테이블에 저장할 수 있고,
이를 Daltons 이라고 부른다.

AminoAcid = {
'A': 'Alanine', 'C': 'Cysteine', 'D': 'Aspartic acid', 'E': 'Glutamic acid',
'F': 'Phenylalanine', 'G': 'Glycine', 'H': 'Histidine', 'I': 'Isoleucine',
'K': 'Lysine', 'L': 'Leucine', 'M': 'Methionine', 'N': 'Asparagine',
'P': 'Proline', 'Q': 'Glutamine', 'R': 'Arginine', 'S': 'Serine',
'T': 'Theronine', 'V': 'Valine', 'W': 'Tryptophan', 'Y': 'Tyrosine',
'*': 'STOP'
}
AminoAbbrv = {
'A': 'Ala', 'C': 'Cys', 'D': 'Asp', 'E': 'Glu',
'F': 'Phe', 'G': 'Gly', 'H': 'His', 'I': 'Ile',
'K': 'Lys', 'L': 'Leu', 'M': 'Met', 'N': 'Asn',
'P': 'Pro', 'Q': 'Gln', 'R': 'Arg', 'S': 'Ser',
'T': 'Thr', 'V': 'Val', 'W': 'Trp', 'Y': 'Tyr',
'*': 'STP'
}
# Here's a new dictionary!
Daltons = {
'A': 71, 'C': 103, 'D': 115, 'E': 129,
'F': 147, 'G': 57, 'H': 137, 'I': 113,
'K': 128, 'L': 113, 'M': 131, 'N': 114,
'P': 97, 'Q': 128, 'R': 156, 'S': 87,
'T': 101, 'V': 99, 'W': 186, 'Y': 163
}
TyrocidineB1 = "VKLFPWFNQY"
# The weight of Tyrocidine B1
print(sum([Daltons[res] for res in TyrocidineB1]))
그리고 이 값들을 더하면 펩타이드 결합으로 아미노산들이 조합된, 하나의 단백질의 분자량을 계산할 수 있다.

길이가 10인 펩타이드 결합은 이렇게 11 C 2 = 55 가지 경우의 수를 가지고 쪼갤 수 있다.
길이가 10인 1개의 조각, 길이가 9인 2개의 2조각, .... 길이가 2인 9개의 조각, 길이가 1인 10개의 조각
RETIRE 이라는 단백질은 RE 라는 조각이 반복적으로 등장한다.
그리고 각각의 부분 조각의 분자량은 중복될 수 있는데,
RETIRE 이라는 단백질에서 RETI, ITIR, TIRE 의 분자량은 모두 499로 동일하다.
이때 모든 펩타이드 결합 체인의 모든 조각 경우의 수에 대해서 유일하게 등장하는 분자량 값의 가짓수를 모은 것을 가리켜 펩타이드의 'Theoretical Spectrum' 이라고 부른다. (자주 나올 표현이다..)
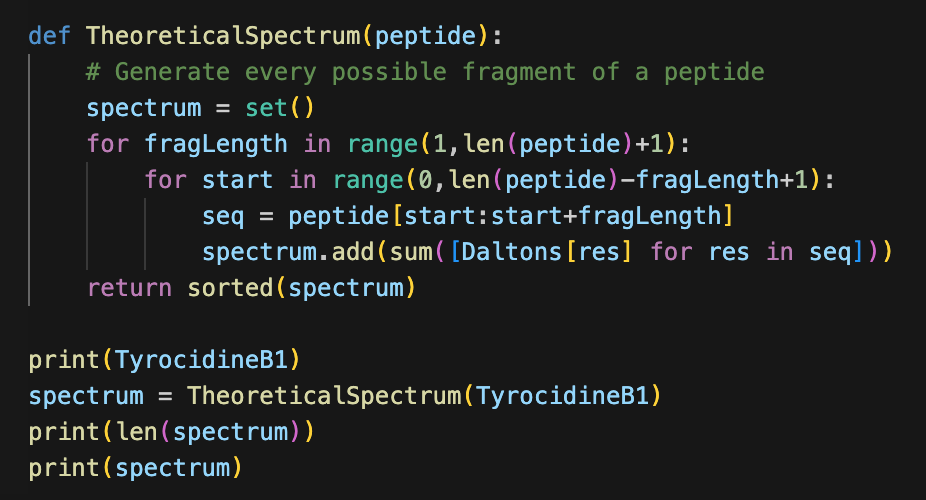
이렇게 집합에 모든 조각에 대해 분자량 값을 계산해서 넣으면 theoretical spectrum을 구할 수 있다.
가능한 최대 가짓수는 (10 + 1) C 2 = 55 였으나, 실제 개수는 51개 임을 확인할 수 있다.
펩타이드 서열이 주어졌을 때, 이로부터 스펙트럼을 구하는 것은 쉽다.
그러면 거꾸로 스펙트럼으로부터 펩타이드 서열을 구하는 건 어떨까?
브루트포스를 생각하려고 해도, 1322 라는 분자량 합을 갖는 펩타이드 조합을 찾는 것은 쉽지 않다.
제일 짧은 길이의 1322와 유사한 값을 만드는 분자량부터 제일 긴 길이의 1322와 유사한 값을 만드는 분자량에 대해서, 각 길이마다 모든 경우의 수를 다 해봐야 할 것이다.
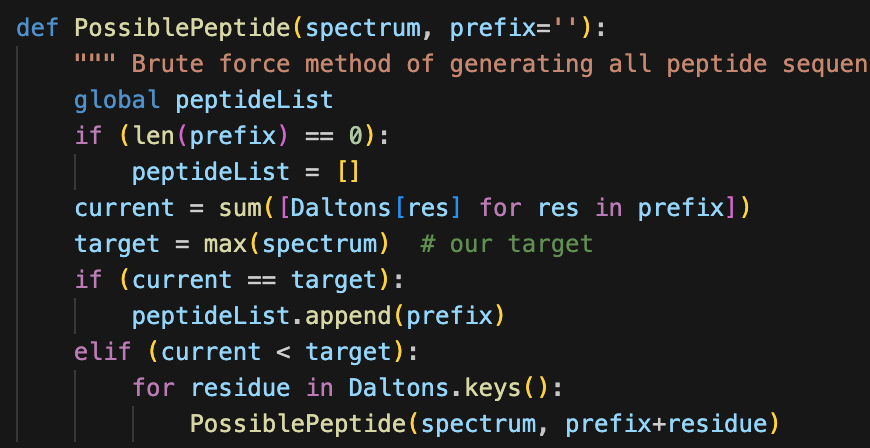
이 코드는 분자량이 1322보다 작다면 아미노산의 모든 조합을 계속 추가하면서 모든 경우의 수를 시도해본다.
이때 spectrum 에서 최댓값만 취급하는데, 이게 길이가 제일 긴 펩타이드 결합의 분자량으로, 우리가 찾는 전체 펩타이드 서열의 분자량이기 때문이다.

그리고 PLAY를 넣었더니 가능한 후보로 그 순서가 뒤집힌 다른 조합도 보여준다.
fragment 로 가능한건 P L A Y PL LA AY PLA LAY PLAY 만 가능하므로, 그 조합들만 나오도록 할 순 없을까?

이건 permutation 이 아니라 combination 의 관점으로 접근하면 해결할 수 있다.
이전의 브루트포스 코드는 permutation을 백트래킹으로 만드는 것과 같았기 때문에 여러개를 만드는 것이다.
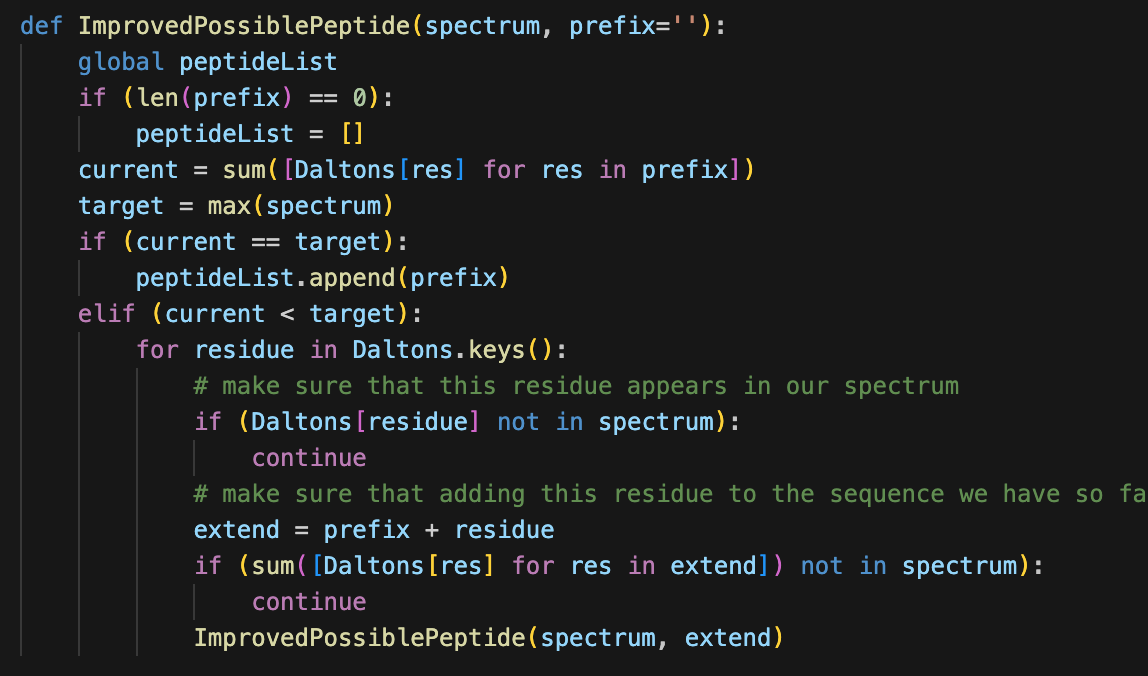
그래서 가지치기 하는 코드를 추가했다.
현재 스펙트럼에 존재하지 않는 분자량을 가진 Dalton이나, extend 조각이라면 더 시도하지 않는다.

그런데도 여전히 우리가 기대하는 서열 외의 서열도 나온다.
지금까지는 'prefix' 에 대해서만 스펙트럼에 존재하는 여부를 체크했기 때문이다.
이제 suffix도 같이 고려해보자.
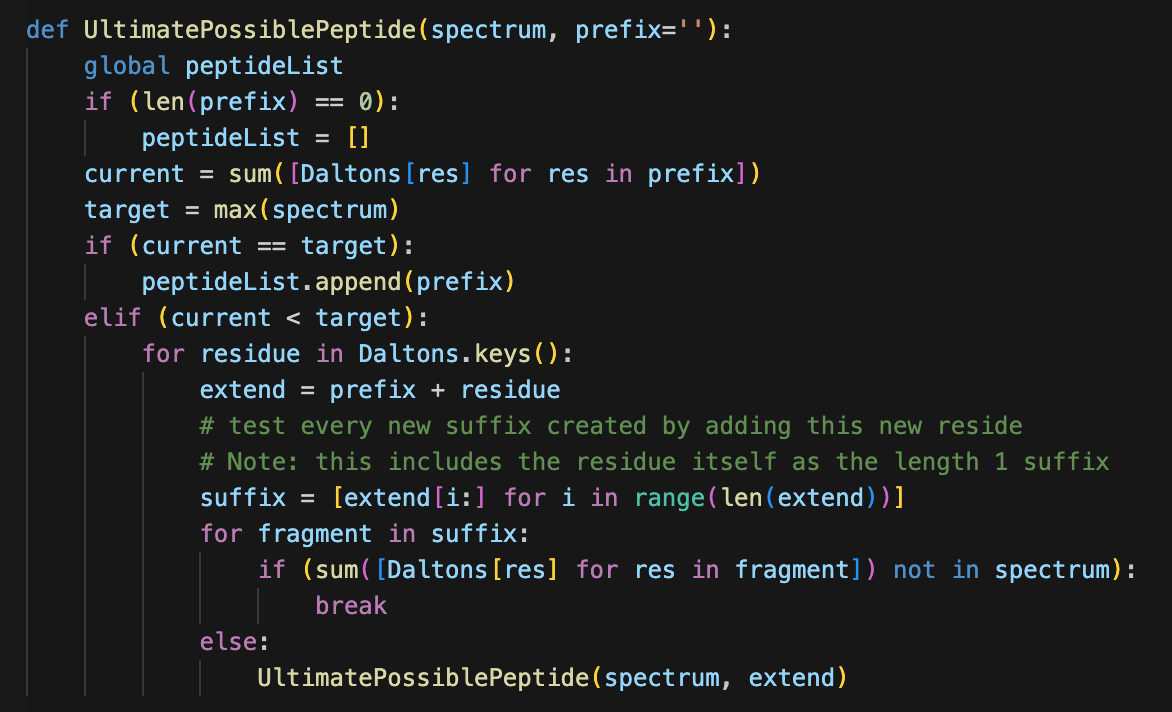
extend를 구성하고, 구성한 extend의 모든 suffix에 대한 분자량이 스펙트럼에 있어야 한다.
이렇게 하면 그 전에 수행한 가지치기 방법보다 더 나은 성능을 보여준다.
(왜 전위는 고려를 안할까? 전위 후위 모두 고려하면 안되나?)
지금까지는 '이론적 스펙트럼'에 대해 아미노산 서열을 추론했다.
그런데 실제로는 측정에 의한 '실험적 스펙트럼' 에 대해 아미노산 서열을 추론하는 경우가 많다.
그런데 실험적 스펙트럼에는 이론적 스펙트럼에 없는 값이 들어가거나, 이론적 스펙트럼에 있어야 하는 값이 누락되기도 한다.
이런 노이즈에 대해서도 좋은 성능을 내는 알고리즘을 만들어보자.
이 알고리즘의 핵심은, 휴리스틱으로 아미노산 서열에 포함될 가능성이 낮은 5%를 제외하는 방식을 사용한다..
(골프 토너먼트 분석에서, 점수가 낮은 일부 선수는 우승할 가능성이 낮다고 보고 후보에서 제외하는 것과 비슷)


하지만 이것만으로는 올바른 답을 찾아내는 것이 완벽하지 않다.
노이즈 정보를 걸러낼 수는 없을까? (이 데이터는 노이즈 일 수 밖에 없다! 싶은 데이터들)
PLAY에서 이론적으로 가능한 모든 조합은 [71, 97, 113, 163, 184, 210, 234, 281, 347, 444]
이 조합에서 71, 163이 제거되었다고 했을 때, 과연 이 리스트를 원복할 수 있을까?

이 스펙트럼 값들은 서로서로의 합으로 만들어질 수 있다.
(예를 들어 PL 은 P와 L의 합으로 만들어질 수 있고, P, L 은 모두 스펙트럼에 존재)
따라서 이렇게 두 스펙트럼 값의 차이 중에서 자주 등장하는 값을 추리면 얘는 혹시 길이가 1인 Dalton이 아닐까? 하는 합리적 의심을 할 수 있다.
(이 테이블을 가리켜서 Spectral Convolution 이라고 부른다고 한다.)

이렇게 만들 수 있고..
이 테이블을 활용해서

기존의 스펙트럼을 '스파이크' 시킬 수 있다.
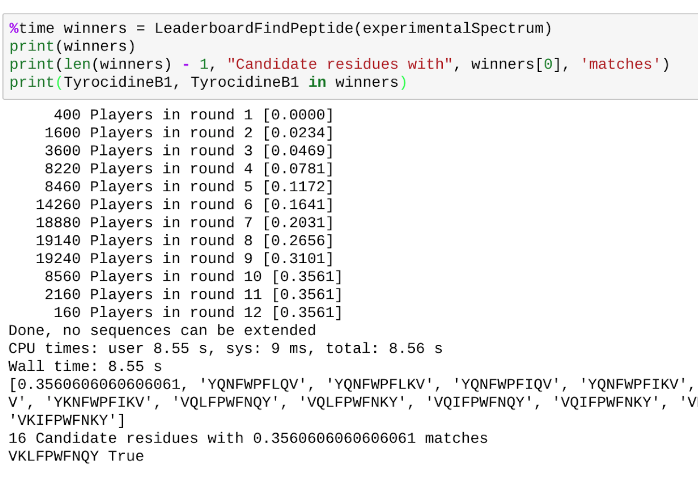
스파이크된 스펙트럼에 대해서 휴리스틱을 돌리면 잘 나온다고 한다..
정리
Daltons : 펩타이드 결합에 참여한 아미노산 서열 '하나' 의 분자량
'Theoretical Spectrum' : 펩타이드 체인을 쪼개는 모든 경우의 수에 대해서 (1개로 쪼개기, 2개로 쪼개기, ... ) 각각 분자량 합을 계산했을 때 등장하는 분자량 값들의 종류
목표 : 이론적 스펙트럼 또는 실험적 스펙트럼이 주어졌을 때, 역으로 펩타이드 결합 서열 복원하기
방법 : 브루트 포스 → 가지치기 → 전위 말고 suffix 고려하기
현실 : 이론적 스펙트럼보다 실험적 스펙트럼에서 결합 서열 복원할 때가 많음
문제 : 실험적 스펙트럼에는 노이즈가 자주 낌
방법 : 휴리스틱, 노이즈 제거하고 휴리스틱
노이즈 제거 방법 : Spectral Convolution 활용하기
Spectral Convolution : 현재 주어진 실험적 스펙트럼 쌍에서 모든 값들에 대해 이차원 배열을 만들고, 각 값들의 차잇값을 저장.
자주 등장하는 차잇값은 이론적 스펙트럼에 존재해야 하는 값일 가능성이 높음.
'CS > 문제해결기법' 카테고리의 다른 글
| 10. 게놈 재배치 (팬케이크 뒤집기 문제) (0) | 2024.12.11 |
|---|---|
| 9. 문자열 패턴 찾기 (6) | 2024.12.11 |
| 7. Assembling a Genome (0) | 2024.10.30 |
| 6. Advanced Sequence Alignment (0) | 2024.10.29 |
| 5. Aligning Sequences (0) | 2024.10.29 |
