지금까지는 CFL을 나내는 기계인 NPDA에 대해 정리했다.
RL에서 DFA와 NFA가 있었던 것처럼, PDA에도 NPDA와 DPDA가 있다.
이번 글에서는 deterministic PDA, DPDA와, 이 기계가 만드는 언어인 DCFL에 대해 정리해본다.
DPDA

새로운 기계를 배우기에 앞서 이제부터 새롭게 배울 기계를 포함하여 지금까지 다룬 기계를 정리해보면 위와 같다.
DFA는 특정 상태에 특정 input symbol 을 읽으면 어떤 상태로 넘어갈 지 반드시 결정할 수 있는, 상태의 개수가 유한한 기계였고,
NFA는 특정 상태에 특정 input symbol 을 읽으면 어떤 상태로 넘어갈 지 결정할 수 없을 수도 있는, 상태의 개수가 유한한 기계였다.
DFA는 트랜지션 함수를 정의할 때 모든 상태와 모든 심볼 조합에 대해서 정의를 해야만 했다면,
NFA는 트랜지션 함수를 정의할 때 λ 를 포함한 모든 심볼과 모든 상태 조합의 subset 에 대해 정의하면 됐었다.
(즉 모든 조합을 명시할 필요 없이, 일부 조합만 명시해도 괜찮았다.)
NPDA는 트랜지션 함수를 정의할 때 모든 상태와 모든 심볼, 모든 스택 심볼의 조합에 대해서 subset 에 대해 정의하면 됐다.
이때 서브셋 표현에서 감마에 *가 붙은 이유는 스택에 데이터를 추가할 수도, 안할 수도 있기 때문에 *로 표시하였다.
DPDA는 NPDA와 같은 상황에서 선택지를 없애기 위해 2가지 조건이 추가되면 된다.
1. 𝛿(q, a, b) 조합에 대해서 갈 수 있는 선택지는 1개이거나 0개여야 한다. (DFA와 다르게 모든 경우가 정의될 필요는 없다.)
2. 만약 𝛿(a, λ, b) 조합에 대해 선택지가 존재한다면, 모든 알파벳 심볼 c에 대해 λ(a, c, b) 조합은 선택지가 없어야 한다.
왜냐하면 스택에서 b를 뺐을 때, a라는 상태에 있었다면 input symbol 을 읽지 않고 이동할 수도 있고, 읽으면서 이동할 수도 있는 선택지가 생겨버리기 때문이다.
(DFA에서는 λ-트랜지션을 허용하지 않았기 때문에 이런 고려사항이 필요하지 않았지만, DPDA에서는 허용하기 때문에 이런 제약이 필요하다.)
여기에서 한 가지 사족을 말씀해주셨는데,
결국 NPDA, DPDA를 만드는 이유는 파싱을 해서 임의로 주어지는 문자열이 어떤 언어에 속하는지 속하지 않는지 빠르게 파싱하기 위해서 만드는 것이다.
그런데 NPDA는 선택지가 여러 개라서 백트래킹을 할 수 밖에 없기 때문에 시간이 오래걸린다.
그렇다면 DPDA는 선택지가 유일하므로 리니어 타임에 파싱을 할 수 있을까?
정답은 할 수 없다!
왜냐하면 리니어 타임에 파싱을 하기 위해서는 매 라운드마다 점점 센텐스에 가까워져야 하는데, DPDA는 트랜지션에 λ 를 허용하기 때문에 매 라운드마다 센텐스에 항상 가까워진다고 말할 수는 없다. 따라서 리니어 타임에 파싱할 수 있다고 장담할 수 없다.
하지만 그럼에도 NPDA보다는 효율적으로 파싱은 할 수 있다.
이로서 DPDA를 정의하였다.
DPDA도 언어를 만들 수 있는데, DPDA 가 만드는 언어는 특별하게 Deterministic CFL 이라고 해서 DCFL 이라고 부른다.
DCFL은 CFL 보다 조금 더 축소된 범위의 언어이다.
(즉, 어떤 언어가 DCFL 이라는 것은, 그 언어를 만드는 DPDA가 존재한다는 것과 같다.)

위와 같은 언어는 CFL의 대표젹인 언어이며, 동시에 DCFL 언어이기도 하다.
DPDA를 만들 수 있기 때문이다.
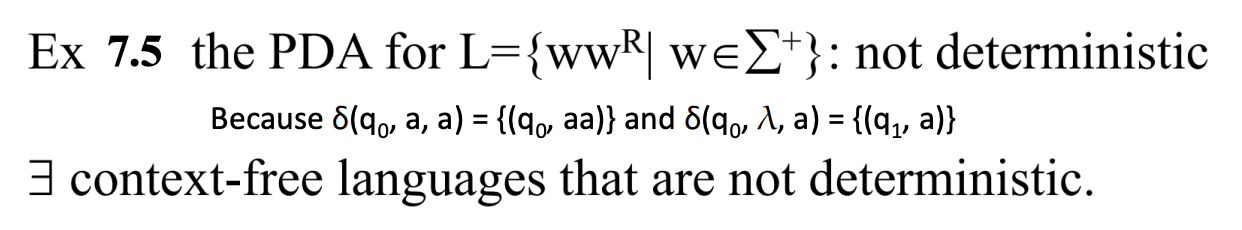
반면 이 언어는 CFL 이지만, DCFL는 아니다.
왜냐하면 (이 문제를 아직 풀어보지는 않았지만) 선택지가 존재하는 트랜지션 함수가 존재하기 때문이다.
이때 언어에 대해서는 NCFL 을 따로 정의하지 않았음에 주의하자.
NPDA가 만드는 언어가 반드시 NCFL 이라고 확정할 수는 없기 때문이다.
NPDA는 DPDA보다 넓은 범위에 있고, 언어의 범위도 NPDA가 만드는 범위가 더 넓다.
따라서 NPDA는 DCFL도 만드고 DCFL이 아닌 언어도 만들 수 있으므로,
NPDA가 만드는 언어는 DCFL이 아니다! NCFL이다! 라고 단정지어 말할 수는 없다.
하지만 결론적으로 예제 7.5가 만드는 언어는 아무리 노력해도 NPDA로 밖에 표현이 되지 않고, DPDA는 존재하지 않는다.
DPDA가 존재하지 않는다면, DCFL이 아니라는 것은 단정지어 말할 수 있다.
(DPDA가 더 좁은 범위에 있기 때문이다.)
이제 두 언어 사이에 이런 차이가 발생하는 이유를 조금 러프하게 더 설명해보면
개수가 같은 지 카운팅 하는 언어의 경우, a와 b의 순서가 정해져있기 때문에, a를 읽고 있다면 전반전, b를 읽고 있다면 후반전이라는 것을 명시적으로 결정할 수 있다.
하지만 7.5 예제의 언어의 경우, 내가 아무리 문자를 읽어도 어디서부터가 후반전의 시작인지를 결정할 수 없다.
즉, 어디까지가 w 이고, 어디서부터가 w^R의 시작인지 확신할 수 없으므로 deterministic 하지 않다.
따라서 기계를 설계할 때, 여기가 후반부라고 생각해고 시도해보고, 여기도 후반부라고 생각해보고 시도해보는 과정을 반복해야 하므로 기계 자체가 deterministic 하지 않다.
그래서 결론을 내보면 NPDA와 DPDA는 equivalent 하지 않다.
(RL 에서는 DFA와 NFA가 equivalent 했던 것과 대조적이다.)
DCFL를 위한 문법
(수업중에는 DPDA와 일치하지는 않는다.. 라고 하셨는데, 슬라이드에는 DCFL을 위한 문법이라고 하셨다.)
DPDA는 NPDA보다 파싱에 더 유리한 형태를 갖고 있다.
현재 상태와 심볼, 스택의 내용에 따라서 어디로 나아갈 지 명확하기 때문이다.
이번엔 DPDA로 만들어지는 언어인 DCFL을 나타내는 문법을 한번 생각해보자.
DCFL을 나타내는 문법은 역시 선택지가 유일해서 파싱에 유리할 것이다.
먼저 이전에 정리했던 글에서 S-grammar 에 대해 정리한 적이 있다.
simple grammar 라고도 했던 이 문법은 진정한 의미의 리니어 타임 파싱을 가능하게 하는 문법이지만, 제약사항이 너무 강해서 표현가능한 언어가 제한적이라는 한계가 있었다.
그래서 컴파일러 분야에서는 LL-Grammar 라는 것을 사용한다.
LL의 뜻은 파싱을 할 때 왼쪽에서 오른쪽으로 스캔하고, 유도는 leftmost derivation 을 사용한다고 해서 LL 이다.
이때 LL(K) Grammar는 k개의 input symbol을 확인하면 하나의 production을 유일하게 결정할 수 있는 문법을 말한다.
즉, S-Grammar보다 확장된 정의를 갖는 문법으로, S-Grammar는 LL(1) grammar 라고도 말할 수 있다.

예제 문제를 풀어보자.
이 문법은 CFG로서, 이 문법이 나타내는 언어는 { aⁿbⁿ : n ≥ 1 } 이다.
또한 a, b 를 각각 여는 괄호와 닫는 괄호로 생각하면 유효한 괄호문자열처럼 생각할 수도 있다.
이 문법은 먼저 S-grammar ( = LL(1) grammar) 가 아니다.
a라는 input symbol 하나를 읽었을 때 aSb, ab 중 어떤 것으로 produce 해야할 지 모르기 때문이다.
하지만 이 문법은 LL(2) 문법이다.
aa 를 읽었다면 aSb 를 선택할 수 밖에 없고
ab 를 읽었다면 ab 를 선택할 수 밖에 없고
bx 를 읽었다면 선택할 수 있는 프로덕션이 없기 때문이다.
그래서 nested 구조의 괄호 형태 문장을 갖는 언어는 LL(2) 문법으로 표현할 수 있다.

주어진 문법은 LL-Grammar 일까?
이 문법은 7.12 예제의 확장된 버전으로 여러개의 nested 괄호 문자열을 나열해서 쓸 수 있도록 확장한 문법이다.
이제 이 문법이 LL-grammar 인지 따져보자.
a 가 하나만 있을 경우, aSb / ab 중에 선택할 수 없으니 LL(1)은 아니다.
aa 를 보는 경우, aSb / SS 중에 선택할 수 없으니 LL(2) 는 아니다.
aaa 를 보는 경우, aSb / SS 중에 선택할 수 없으니 LL(3) 은 아니다.
...
따라서 주어진 문법은 모든 k 에 대해 LL(k) 문법이 될 수 없으므로, LL-Grammar 가 아니다.

참고로 위와 같이 쓰면, 같은 문장을 만들어내는 LL-grammar를 만들 수 있다.
'CS > 오토마타' 카테고리의 다른 글
| [오토마타] 22. CFL의 Closure Property (0) | 2024.12.12 |
|---|---|
| [오토마타] 21. Pummping Lemma (for CFL) (0) | 2024.12.12 |
| [오토마타] 19. NPDA & CFL (0) | 2024.12.12 |
| [오토마타] 18. NPDA (0) | 2024.12.11 |
| [오토마타] 17. 문법 변환 - Normal Form (0) | 2024.12.10 |
