Pumming Lemma
RL와 관련된 Pummping Lemma 를 정리하면서, 펌핑 레마를 통해 이 언어가 적어도 RL는 아니다! 라는 것을 보일 수 있다고 하였다.
CFL에도 펌핑 레마가 있다. 그리고 결론만 말하면 CFL에서도 펌핑레마를 통해 이 언어가 적어도 CFL은 아니다! 라는 것을 보일 수 있다.
RL에서는 어떤 문장을 3조각 내서 펌핑레마를 적용했다.
CFL에서는 어떤 문장을 5조각 내서 펌핑레마를 적용한다.
RL에서 유한집합의 언어라면 RL인지 판별하는 것이 쉽다고 했었다. (정리글 참고)
같은 이유로 CFL에서도 유한집합의 언어라면 CFL인지 판별하는 것이 쉽다.
따라서 RL에서 그러했듯, 이번에도 무한집합인 CFL에 대해서만 판별하는 방법을 생각해본다고 하자.
CFL의 크기가 무한집합이라면 그 안에는 길이가 매우 긴 문장이 적어도 1개는 반드시 존재한다.
이때 이 문장의 길이가 m 이상이라고 해보자.
그러면 이 문장을 uvxyz로 5조각을 낼 수 있다.
이때 가운데 세조각의 길이를 m ≥ |vxy| 라고 하고, |vy| ≥ 1 이라고 하자.
이 조건을 만족하도록 쪼갰다면, 2번째 조각인 v와 4번째 조각인 y를 똑같이 펌핑 업/다운 했을 때도 여전히 L에 속한다.
즉 uvⁱxyⁱz 는 여전히 L의 문장이다.
RL에서는 상태의 개수가 유한하기 때문에, 무한한 언어를 표현하려면 반드시 사이클이 존재할 수 밖에 없고 (비둘기집 원리)
이 사이클을 기준으로 펌핑 업/다운을 해도 여전히 문장이 된다고 할 수 있었다.
CFL에서는 이 언어를 표현하는 문법에서 '변수'의 개수가 유한하기 때문에 무한한 언어를 표현하려면 반드시 적어도 하나의 변수를 여러 번 거칠 수 밖에 없다는 점을 이용한다.
이를 증명하기 위해, 다음과 같이 derivation tree 를 그려보자.

그러면 이렇게 시작변수로부터 뭔가 파싱을 잘 해서 트리를 다 그렸다면, 마지막에 리프노드에는 항상 터미널이 남았을 것이고,
이 터미널 리프노드를 왼쪽에서부터 읽은 yeild 가 이 문법이 만드는 언어가 되었다.
이때 이 그림을 조금 단순화해서 이렇게 그릴 수 있다.

S 라는 변수를 윗 꼭짓점으로 삼각형을 그렸을 때,
S라는 삼각형에 포함되는 터미널 t1, t2, t3가 S라는 변수로부터 유도된 문자열이라고 할 수 있다.
이제 유도 과정에서 중간에 변수도 있고, 하다보면 다음과 같이 트리를 그릴 수 있다.

이 트리는 S라는 시작변수로부터 uvxyz 라는 문장이 나오고,
A라는 S 밑의 변수는 vxy라는 문자열을 만들어내고, 그 밑의 A라는 변수는 x라는 문자열을 만든다고 표현할 수 있다.
그리고 이 '문장' 의 길이는 m 이상이라고 해보자.
그런데 문장이 매우 김에도 불구하고, 변수의 개수는 유한해서, 필연적으로 반복되는 변수가 등장할 수 밖에 없다.
(위 그림의 트리에서 A가 반복됨을 알 수 있다.)
먼저 문법의 경우에는 λ-free Grammar를 생각한다.
또한 λ-production, unit-production은 없다고 해보자. (문법 변환에서 본 것처럼 equivalent 하도록 유지하면서 없앨 수 있다.)
이제 충분히 긴 문장에 대한 derivation tree 를 생각보자. 이 트리의 높이는 충분히 높다고 할 수 있다.
그러면 위 그림에서 보는 것처럼 변수는 필연적으로 반복되므로, 문장을 5조각으로 쪼갰을 때 위 그림과 같이 derivation tree를 표현할 수 있다.
(A가 vxyz 를 포함할 수도 있지 않냐, 저렇게 된다는 보장이 어디있냐, 라고 할 수 있겠지만, 위에서 보는 조각은 터미널 '스트링'이다. 만약 S → uA 와 같은 프로덕션이었다고 하면 z = λ 로 두면 될 뿐, 위 그림과 같이 일반화해서 표현하는데는 문제가 없다. 사실 내가 의문이 들어서 자문자답한 것..)
A 밑에 한번 더 A가 등장할 때는 직접 등장해도 되고, 다른 변수를 여러번 거처서 등장해도 되나, 어쨌든 중요한 것은 A가 한번 더 등장했다는 것이 중요하다. 그리고 트리에서 나중에 등장한 A는 맨 처음에 등장한 A보다 만들어내는 문장의 길이가 작을 수 밖에 없다. (unit-production, λ-production은 없다고 했으므로)
이 트리만 놓고 보면 적어도 다음과 같은 느낌의 derivation은 반드시 존재할 것임을 알 수 있다.
S =>* u A z
A =>* v A y | x
이때 A는 언젠가 자신을 포함하는 폼을 유도한다는 것이 핵심이다.
왜냐하면 내가 유도한 폼 속의 A에서도 또 A를 포함한 폼을 유도하면 그것이 pumping up 이고,
내가 유도한 폼 속의 A에서 x를 유도하도록 끝내면 그것이 pumping down 이기 때문이다.
pumping up을 하게 되면 v, y 가 추가적으로 늘어나고
pumping down을 하게 되면 v, y 가 감소한다.
하지만 그렇게 변환된 문자열 역시 여전히 L의 문장이다.
이때 |vy| ≥ 1 인 이유가 여기서 등장한다.
이 문법에는 unit-production이 없기 때문에, A =>* A 는 존재할 수 없기 때문이다.

이 그림은 기존의 트리에서 펌핑 다운한 모습과 펌핑 업한 모습을 보여준다.
왼쪽은 v, y 가 사라졌고, 오른쪽은 v, y 가 추가된 것을 알 수 있다.

이제 예시를 하나 살펴보자.
이 문법은 CNF 문법으로, A라는 시작 변수에서부터 시작하여 bbbaba 라는 문장을 유도하는 과정을 보여준다.
그 유도 과정을 derivation tree 로 표현하면 위와 같다.
이때 A에서 A가 반복되고 있으므로 그 과정을 기준으로
A =>* b A ba | bbCλ | a라고 표현할 수 있다. (구분을 위해 람다를 임의로 표현하였다.)
즉, 기존의 uvxyz 노테이션을 활용하면 u = b, z = ba, v = bb, y = λ, x = a 이다.

그림으로는 이렇게 그릴 수 있다.
그리고 펌핑 업/다운을 통해 i 부분을 늘리거나 줄여서 여전히 같은 언어에 속하는 문장을 만들 수 있다.
그리고 이는 이 언어가 CFL 일 때 성립한다. 따라서 이 펌핑 렘마를 적용할 수 없다는 것은 곧, CFL이 아님을 의미한다.
(펌핑 렘마가 통한다고 CFL이라는 것은 아니다. 하지만 펌핑 렘마가 안통하면 CFL은 아니라는 것)
Example 1

주어진 언어가 CFL이 아님을 펌핑렘마를 통해 증명해보자.
증명 과정은 RL에서 했던 것처럼, 상대방과 내가 왔다갔다 제시하는 방법으로 증명하면 된다.

먼저 상대방은 CFL임을 주장한다.
그러면 펌핑렘마가 된다는 것을 의미하므로,
나는 상대방에게 펌핑렘마 안되는 거 보여줄테니, 펌핑렘마에서 필요한 기준인 충분한 크기의 m을 달라고 요구한다.
상대방이 m을 제시하면, 나는 m 이상의 길이를 갖는 문장을 하나 제시한다.
CFL이라면 펌핑렘마는 길이가 m이상인 모든 문장에 대해서 적용 가능해야 한다.
이때 나는 문장으로 aᵐbᵐcᵐ 을 제시하였다.

상대방은 이 문장에 대해 펌핑렘마가 가능하도록 5등분으로 쪼개기를 시도한다.
5등분으로 쪼갤 때는, 가운데 3조각의 길이가 m 이하여야 하고, v와 y의 길이 합이 1 이상이어야 한다.
하지만 a, b, c 각각의 개수가 m 이상이기 때문에, m 이하의 크기를 갖는 윈도우를 아무리 옮겨도 a, b, c 세 가지를 모두에 담는 것은 불가능하다.
이게 불가능하면 안되는 이유는 vxy 에서 v와 y가 동일하게 증가/감소할 때 전체 a,b,c의 개수도 동일하게 증가/감소해야 한다.
그러려면 vy 에 a,b,c의 개수가 동일하게 들어있어야 함을 의미한다.
하지만 이렇게 만드는 것은 불가능해서 어쩔 수 없이 v = aᵏ, y = bᵏ 를 제시했다고 해보자.

이때 k 는 0이 될 수 없고, 위와 같이 펌핑 다운을 했을 때 a, b, c의 개수가 다르다는 점을 보여주면 CFL이 아님을 증명하는데 성공한다.
(CFL이었다면 상대가 어떻게든 펌핑렘마가 가능한 케이스를 제시했을 것이므로)
Example 2

w는 임의의 a, b로 구성된 스트링인데, 그냥 그거를 동일하게 복사해서 옆에 붙인 언어에 대해 CFL이 아님을 증명해보자.
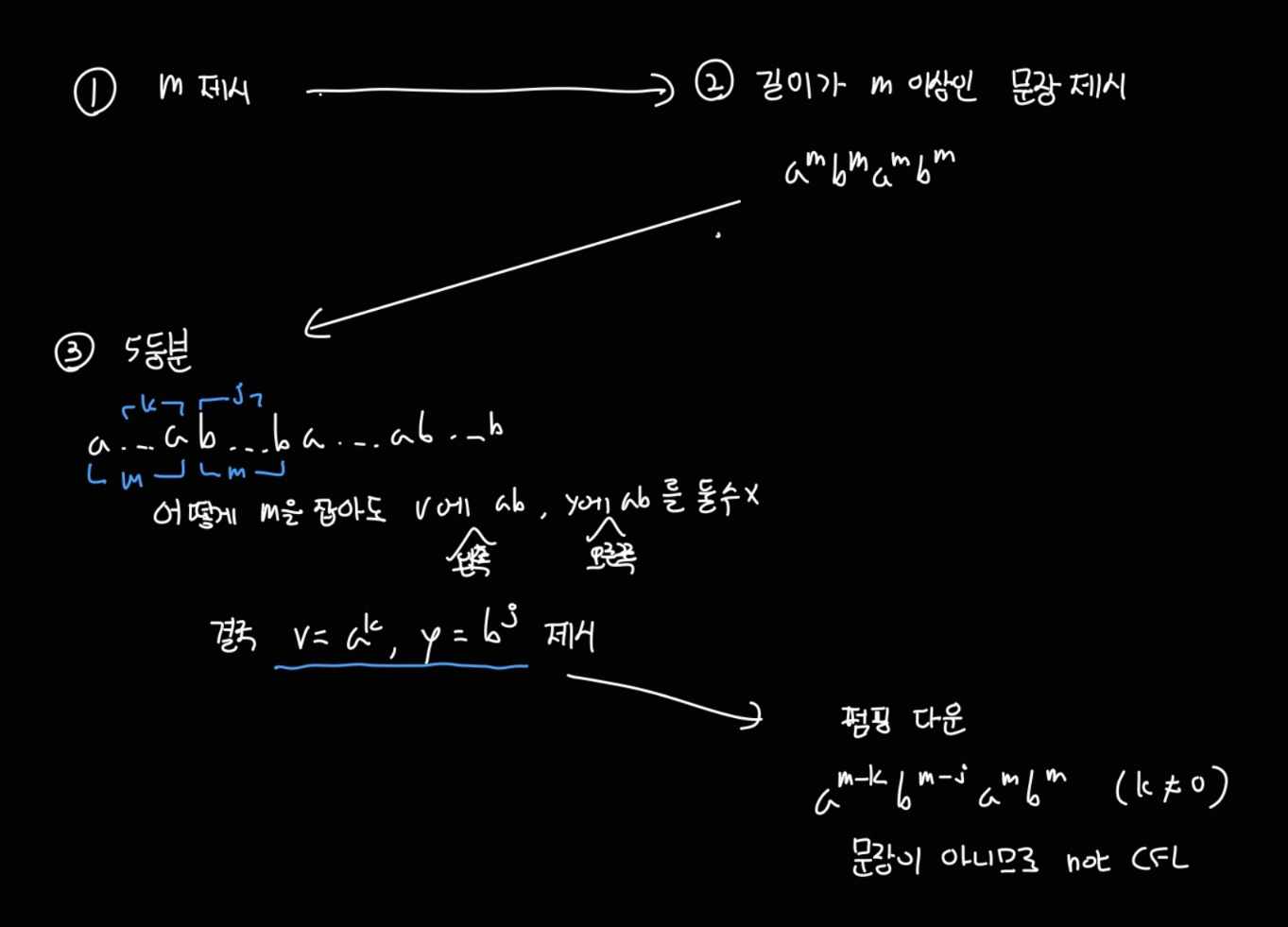
결국 펌핑렘마를 통한 증명의 핵심은 길이가 m 이상인 문장을 잘 제시하는 것
(그런데 그 문장에서 어떻게 5등분을 해도 성공할 수 없음을 증명하는게 어려운 것 같다. 모든 5등분 경우의 수를 다 해볼 수는 없는 노릇이니...)
위와 같은 과정으로 증명할 수 있다.
Example 3
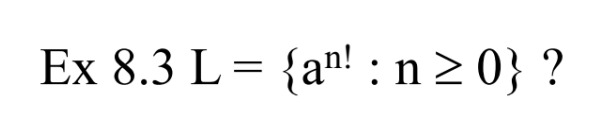
a가 n! 개 존재하면 문장인 언어이다.
이 언어도 CFL이 아님을 증명할 수 있다.

어차피 a 밖에 없기 때문에 상대방이 v, y 를 제시할 때는 a로만 이루어진 문자열을 제시할 수 밖에 없다.
이번 예제의 증명의 핵심은 상대방이 제시한 문자열에 대해 pumping down 했을 때, 이 문장이 기존 문장이 될 수 없음을 증명하는 것이다.
이를 위해 m! - k - j 가 m! 과 (m-1) ! 사이의 어딘가에 존재하는 값임을 보여서
절대 팩토리얼 꼴로 나타낼 수 없음을 증명하여 문장이 아님을 증명하였다.
Example 4

(수업시간에 풀어주시지는 않았다. 나중에 따로 풀어볼 예정)
'CS > 오토마타' 카테고리의 다른 글
| [오토마타] 23. Standard Turing Machine (0) | 2024.12.12 |
|---|---|
| [오토마타] 22. CFL의 Closure Property (0) | 2024.12.12 |
| [오토마타] 20. DPDA & DCFL (0) | 2024.12.12 |
| [오토마타] 19. NPDA & CFL (0) | 2024.12.12 |
| [오토마타] 18. NPDA (0) | 2024.12.11 |
