지금까지 RL, CFL 을 다루었지만, 그것에도 속하지 않는 언어들이 있었다.
예를 들면 aⁿbⁿcⁿ 과 같은 언어나, ww 와 같은 언어가 있었다.
그렇다면 이런 언어들은 기계로 표현할 수 없을까?
저장공간이 스택이 아니라 다른 형태의 저장공간을 쓰면 이런 언어를 기계로 표현할 수 있지 않을지 생각해볼 수 있다.
그래서 이런 언어를 표현하기 위한 새로운 기계로 Turing Machine 을 알아보자.
Turing Machine

튜링 머신은 위와 같은 구조로 되어있다.
튜링 머신에는 input file 이 별도로 없고, 컨트롤 유닛과 매우 긴 테이프가 하나 존재한다.
테이프의 셀 하나에는 '테이프 심볼'이 하나 들어간다.
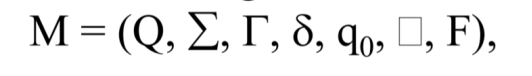
튜링머신은 위와 같이 정의한다.
PDA에서 감마(Γ)는 스택 심볼이었다면, 튜링머신에서는 테이프 심볼을 나타낸다.
이때 인풋 심볼(Σ)이 정의되어 있는데, 이 인풋 데이터 역시 테이프에 들어있다.
또한 테이프에는 blank 라는 것이 들어갈 수 있는데, 이를 나타내는 심볼이 블랭크 심볼로서 ㅁ에 해당한다.
블랭크 심볼은 테이프 심볼이지만, 인풋 심볼은 아니기 때문에, 결과적으로 인풋 알파벳은 테이프 알파벳에서 블랭크 심볼을 제외한 집합의 부분집합이라고도 볼 수 있다.

튜링머신의 델타 펑션은 위와 같이 정의한다.
정의역은 상태와 테이프 심볼의 조합이고, 이로부터 나오는 결과는 (상태, 테이프 심볼, L/R) 의 조합이다.
상태는 변화할 상태, 테이프 심볼은 변화 후 테이프에 입력할 내용,
L과 R은 현재 테이프에서 데이터를 읽는 포인터를 왼쪽으로 한칸 옮길 지, 오른쪽으로 한칸 옮길지를 나타낸다.
또한 NPDA와 다르게, 결과가 유일하게 하나이므로, 이 기계는 deterministic 하다.
또한 델타 펑션은 partial function 으로, 모든 조합에 대해 다 기술하지 않아도 된다.
따라서 만약 기계가 동작하다가 정의된 트랜지션 함수가 없어서 동작할 수 없는 경우, 기계가 halt 되었다고 말한다.
(기계가 종료된다고 생각하면 된다.)
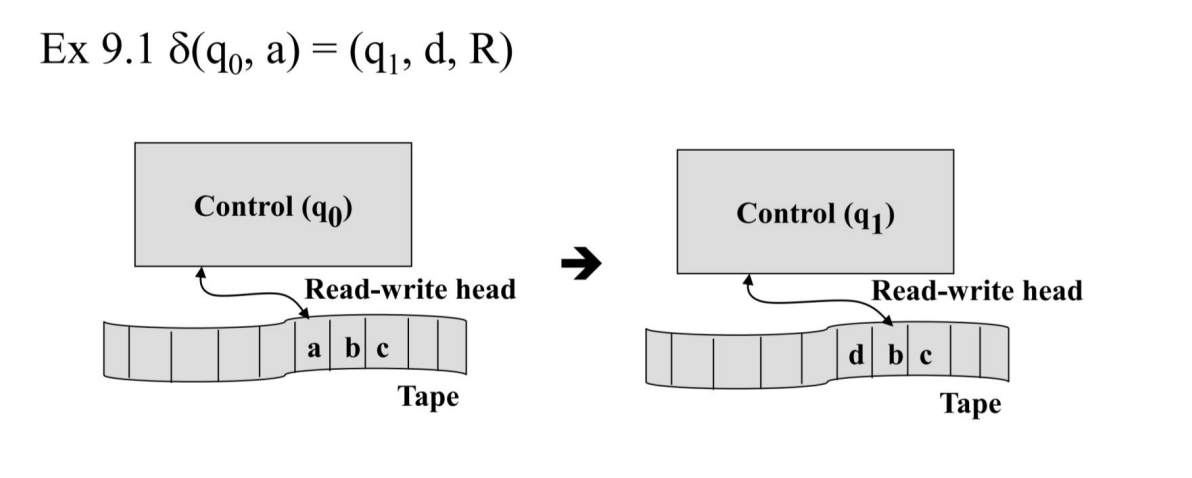
예제 9.1을 보면, 먼저 기계가 시작했을 때 초기 상태는 q0 이고, 인풋 테이프에는 블랭크가 쭉 들어있다가 abc 가 들어있고, 처음에는 a를 가리키고 있다고 해보자.
위 예제의 트랜지션 함수는 q0 상태에서 a를 읽었을 때, q1 상태로 변화하고, 현재 위치에 d를 쓴 뒤, 오른쪽으로 한칸 이동하는 트랜지션 함수를 보여준다.
그림으로는 위와 같이 그려진다.

위와 같은 튜링머신이 있다고 해볼 때, 트랜지션 함수들을 살펴보면
q0 상태에서 a를 읽으면 상태는 유지하되, 현재 위치에 b를 쓰고 한칸 이동
q0 상태에서 b를 읽으면 상태를 유지하되, 현재 위치에 b를 계속 두고 한칸 이동
q0 상태에서 블랭크를 만나면 상태를 q1으로 이동하고 블랭크를 계속 둔 뒤 왼쪽으로 이동한다.
결과적으로 모든 a를 b로 바꾸고, 문장의 끝을 만나면 (블랭크를 만나면) 상태를 q1으로 바꾸고 문장의 끝을 가리키면서 기계가 멈춘다. (halt) 더이상 q1 에서 a또는 b를 읽었을 때 할 수 있는 동작이 없기 때문이다.
문제에서 기술한 기계를 보면 현재 q1은 final state 인데, 튜링머신은 보통 q1 (final) 상태에서는 halt 되도록 트랜지션 함수를 기술하지 않는 것이 일반적이다. (자기 자신으로 들어오는 트랩조차 없어야 한다.)

그래서 기계의 동작을 위와 같이 표현할 수 있고, 트랜지션 그래프로 그리면

이렇게 그릴 수 있다.
q0 에서 a를 읽었을 때, b를 쓰고 R로 이동한다 와 같이 (a, b, R) 을 적어주면 된다.
final state로 갈 때는 블랭크를 읽었을 때, 블랭크를 쓰고, 왼쪽으로 간다고 기술하면 된다.

위 예시로 나타난 튜링 머신을 트랜지션 그래프로 그려보면 아래와 같다.
이때 final state 가 없음에 유의하자.

이렇게 그릴 수 있다.
위 그림을 보면 a를 읽은 다음에는 오른쪽으로 가고 q1 상태로 전이
b를 읽은 다음에는 왼쪽으로 가고 q0 상태로 전이
이를 무한 반복하므로, ab를 계속해서 왔다갔다하는 형태로 동작하며, 포인터는 한쪽 방향으로 두 칸 이상 움직이지 않는다.

정리를 해보면, 스탠다드 튜링 머신은 다음과 같은 3가지 특징을 갖는다.
1. 튜링 머신은 무한한 길이의 테이프를 가지므로, 몇 번이든 왼쪽/오른쪽으로 이동할 수 있다.
2. 튜링 머신은 델파 함수가 각 configuration (튜링머신의 현재 상태) 에 대해서 하나의 move 만 정의하므로 deterministic하다.
3. 튜링 머신은 특정한 input file, output file 이 없으며, 초기 테이프의 일부가 input이되고, halt 되었을 때의 테이프의 일부가 output 이 된다.
Move
튜링머신에서의 move는 NPDA에서 정의했던 것과 똑같이 instantaneous description(앞으로 줄여서 i.d 라고 쓰겠다..) 을 가지고 표현할 수 있다.
i.d 는 현재 튜링머신의 configuration을 압축적으로 보여주는 것으로, 다음과 같은 정보가 필요하다.
1. 현재 컨트롤 유닛의 상태
2. 현재 테이프의 데이터
3. 현재 테이프의 헤더 (포인터) 위치

NPDA에서는 여러가지 정보를 3-튜플로 묶어서 표현했다면,
튜링머신에서는 이 정보를 한번에 묶어서 표현한다.
위와 같은 상황을 i.d 로 나타내면, a1 ~ an 까지 n개 데이터가 테이프에 들어있고, 그 앞뒤로는 모두 블랭크가 들어있다고 할 때
a1a2...a_(k-1) q ak a_(k+1) .... a_(n)
와 같이 표현할 수 있으며,
특히 q를 기준으로 앞 뒤를 하나의 문자열로서 x q y 와 같이 표현할 수도 있다.
현재 헤드가 가리키고 있는 문자는 q의 오른쪽에 포함된다는 것만 주의하면 어렵지 않다.

만약 테이프에 abcd가 있을 때 위와 같은 델타 함수에 의해 move가 발생한다면 그 move는
ab q1 cd ├ abe q2 d 와 같이 된다.
헤더가 오른쪽으로 한칸 이동하였고 기존의 c가 e로 대체되면 된다.

예시를 하나보면
현재 q0 상태에서 테이프에 aa 만 들어있고 왼쪽의 a를 헤더가 가리키고 있는 상황에서,
오른쪽으로 한칸 이동하며 a를 b로 바꾸고 상태를 유지하는 트랜지션 함수가 있다면
q0 aa ├ b q0 a 와 같은 move를 표현할 수 있고
다시 반복하면
b q0 a ├ bb q0 ㅁ 와 같이 move를 표현할 수 있고,
만약 블랭크를 읽으면 q1으로 바꾸고 왼쪽으로 포인터를 이동한다고 하면
bb q0 ㅁ → b q1 b 가 되고나서 기계는 멈춘다. (halt)
(q1 오른쪽에 b가 있으니 현재 q1상태에서 b를 가리키고 있는 그림으로 표현할 수 있다.)
그리고 이런 move를 연속적으로 표현하여
q0 aa ├* b q1 b 와 같이 줄여서 쓸 수도 있다.

그래서 L, R 이동과 관련된 트랜지션 함수에 대해 move 가 어떻게 변화하는지 기술한 것이 위 내용이다.

이 내용은 halt 에 대한 설명을 보여주는데, 트랜지션 함수가 정의되어 있지 않은 상태와 심볼 조합까지 move 하고 멈춘 것을 가리켜 halt 되었다고 한다.

그리고 computation 이라는 용어가 새로 등장하는데, 이 용어는 halt state로 빠질 때까지 configuration을 나열한 서열을 말한다.
TM as Language Acceptor vs Transducer
Acceptor
맨 처음에 오토마타를 정의할 때, 기계에는 크게 Acceptor 와 Transducer 가 있다고 했었다.
지금까지 본 기계는 모두 Acceptor 였는데, 튜링머신은 지금까지 본 것처럼 Acceptor 로 동작할 수도, Transducer로서 동작할 수도 있다.
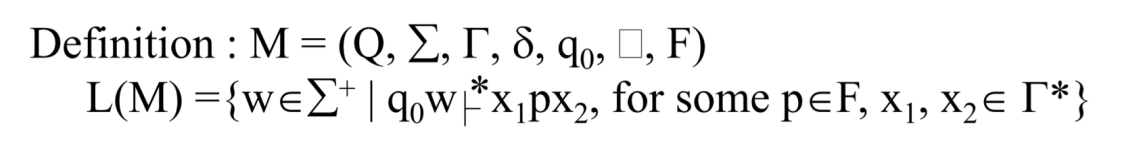
이 정의는 Acceptor 로서 동작하는 튜링머신이 만드는 언어 L(M)을 정의한 것이다.
튜링 머신이 만드는 언어는 '인풋 심볼' 을 1개 이상 나열해서 만든 문자열(λ 는 안됨)로, q0 상태에서 문자열을 테이프에 넣은 다음 기계를 동작하면 기계는 x1 p x2 상태로 가고, 이때 p 는 final state 이면 된다.
이때 람다를 허용하지 않는 이유는 람다와 테이프 심볼 중 블랭크 심볼을 구분할 수 없기 때문이다.
즉, 결과적으로 기계가 halt 되었을 때, final state로 halt 되었는지만 중요하고,
그때 테이프에 어떤 값이 들어있고, 어디를 가리키고 있는지는 중요하지 않다.

위 두 언어는 하나는 CFL이고 하나는 CFL이 아니었다.
두 언어를 모두 TM으로 표현해보자.
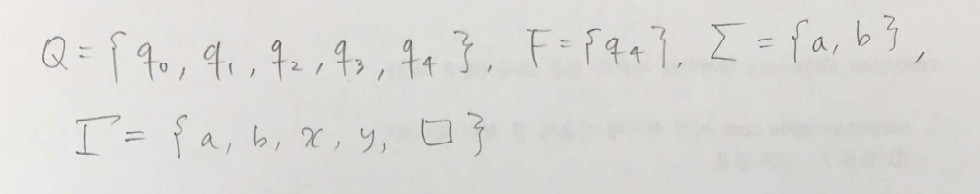
먼저 9.7 예제를 나타내보기 위해, 상태, final state, input symbol alphabet, tape alphabet 을 위와 같이 정의했다고 해보자.
NPDA에서는 스택을 활용해 a를 만나면 1을 넣고, b를 만나면 1을 빼는 식으로 문제를 풀었다.
그리고 모든 인풋 심볼을 다 읽었을 때, 스택이 비어있다면 문장으로 판단할 수 있었다.
튜링 머신에서는 스택 대신에 테이프가 있을 것이고, 테이프에는 블랭크와 블랭크 사이에 판별할 문자열이 들어있다고 해보자.
그리고 초기에는 헤더가 문자열의 첫번째 글자를 가리키고 있다.
튜링머신에서는 문장을 판별할 때 아래와 같이 판별하도록 할 수 있다.

먼저 기본적인 아이디어는 이렇게 aaabbb가 있을 때, 첫번째 a와 첫번째 b를 묶고, 그 다음에도 묶는 식으로 페어링을 한다.
그리고 페어링을 하다가 모두 다 페어링해서 문장이라는 확신이 생기면 그때 halt 하는 것이다.
이 전략을 트랜지션 함수로 구현해보면
먼저 q0는 초기상태로, a를 읽으려는 상태이다.
따라서 𝛿(q0, a) → (q1, x, R) 과 같이 표현할 수 있다.
이때 a를 x로 대체하는 이유는 지금 이 a가 읽어서 사용한 a인지, 아직 사용하지 않은 a인지 구분이 필요하기 때문이다.
q1 상태는 a를 하나 읽었고, 그 쌍이 될 b를 찾으려는 상태이다.
따라서 𝛿(q1, a) → (q1, a, R) 과 같이 표현하여 a를 읽었으면 교체하지 않고 오른쪽으로 헤더를 옮긴다.
만약 b를 읽었다면 𝛿(q1, b) → (q2, y, L) 과 같이 쓸 수 있다.
b를 읽은 상태에서는 드디어 쌍을 찾았으니 q2 라는 상태로 바꾸고 읽은 b는 읽지 않은 b와 구분하기 위해 y로 바꿔준다.
이제 다시 왼쪽으로 가서 a를 찾아야 한다.
q2 상태는 읽지 않은 제일 왼쪽의 a를 찾는 과정이다.
따라서 𝛿(q2, a) → (q2, a, L) 로 표현하여 일단 a를 만나면 왼쪽으로 이동한다.
제일 왼쪽의 a를 사용해야 하기 때문이다.
만약 y가 쌓여있었다면 y를 거쳐서 a가 있는 영역으로 돌아가야 할 수도 있다.
따라서 𝛿(q2, y) → (q2, y, L) 도 필요하다.
제일 왼쪽의 a를 읽고 헤더를 왼쪽으로 옮겼다면 그 다음에는 q2 에서 x를 읽었을 것이다.
따라서 𝛿(q2, x) → (q0, x, R) 로 표현하여 x를 유지한 채 방향을 바꿔주고 a를 읽으려는 상태인 q0로 이동한다.
다시 q0 에서 a를 읽었다면 동일한 b를 찾는 과정을 수행할텐데, 이떄 한가지 트랜지션이 더 필요하다.
바로 𝛿(q1, y) → (q1, y, R) 이다.
제일 왼쪽의 a와 제일 왼쪽의 b를 페어링 했기 때문에, 그 다음 b를 찾는 과정에서는 y를 지나칠 수 있다.
따라서 y는 무시하고 넘어가도록 하는 트랜지션이 추가로 필요하다.
b를 읽는데 성공했다면 왼쪽으로 되돌아오는 과정을 동일하게 반복할 것이다.
이제 판별과 관련된 트랜지션을 써주자.
먼저 모든 a를 읽었는데, b가 부족하다고 해보자.
그러면 b를 찾으려는 q1 상태에서 a 또는 y를 타고 이동하다가 블랭크를 만났을 것이다.
이 경우에는 final state 가 아닌 채로 halt 되어야 한다. 따라서 트랜지션을 정의하지 않는다.
다음으로 모든 a를 읽었는데, b가 남았다고 해보자.
그러면 다음으로 a를 찾기 위해 왼쪽으로 되돌아와서 x를 만나 오른쪽으로 꺾었을 때, y가 있었다는 뜻과 같다.
(xxyyb 인 상황에서 x를 만나 오른쪽으로 틀었는데, a가 아니라 y를 읽은 상황)
이때도 트랜지션을 정의하지 않아서 halt 시키면 된다.
그렇다면 명시적으로 상태를 바꿔서 final state로 이동해야 할 상황은 언제일까?
< q0 상태에서 a를 찾기 위해 오른쪽으로 이동하던 중 y 를 만난 경우 >
이때는 모든 a를 다 소비한 상태다. 따라서 q3 이라는 새로운 상태로 바꾸고, 모든 y를 지나 오른쪽으로 이동한다.
𝛿(q0, y) → (q3, y, R)
𝛿(q3, y) → (q3, y, R)
이렇게 이동하다가 blank 를 만났다면 모든 a-b 쌍을 처리한 것이다.
따라서 이때 final state로 이동하면 된다.
𝛿(q3, ㅁ) → (q4, ㅁ, R)
사실 마지막에는 방향이 중요하지 않다.
어차피 q4 에서는 아무런 트랜지션이 정의되지 않기 때문이다.
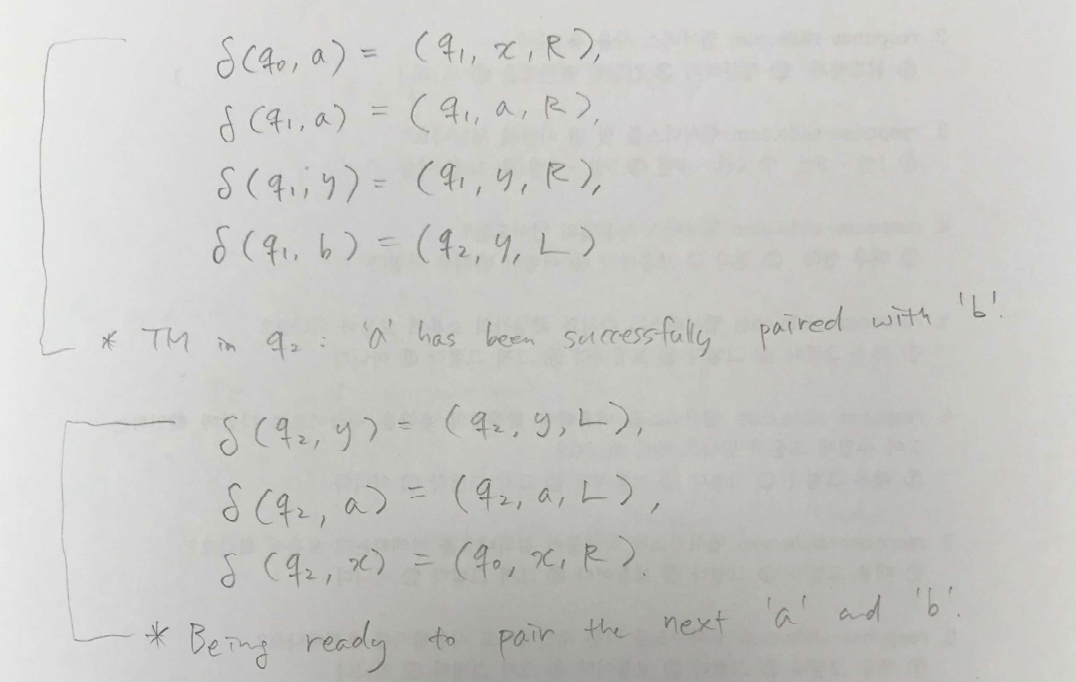

위 설명에 맞춰 정의한 기계는 위와 같다.

이 기계에 aabb 와 aab를 넣고 실행해보면 그 computation 결과는 위와 같은 move 의 시퀀스로 표현된다.
그 밑의 9.8 예제는 같은 방법으로 수행하면 되지만 복잡해져서 생략하셨고,
이런 류의 튜링 머신 만들기 문제는 시험에는 내지 않는다고 하셨다.
Transducer
마지막으로 TM이 transducer 로서 동작한다는 것은 Acceptor 처럼 Yes/No 를 리턴하는 것이 아니라 String 을 output으로 내보내는 기계를 말한다.
예를 들어 계산기는 10 + 20 이 들어오면 30 이라는 결과를 출력해주어야 하므로 transducer 라고 할 수 있다.

여기에서 turing computable 이라는 용어를 새로 정의할 수 있다.
이 말은 어떤 문장w을 받아들이는 함수 f 에 대해서 f(w) 가 연산 결과로 존재할 때
튜링머신의 q0 상태에서 w이 테이프에 들어있는 상태에서 computation을 진행한 결과 pf(w) 가 되었다면
즉, final state p로 도착했고, 그때 테이프에서 f(w) 를 헤더가 가리키고 있었다고 해보자.
이게 모든 w에 대해 성립하는 함수 f 를 가리켜 turing computable 이라고 말한다.
즉 f는 입력으로 w 라는 input을 주면 output 으로 f(w) 를 내보내는데,
튜링 머신에 w를 주고 돌리면, halt 되었을 때, f(w) 가 테이프에 남아있는 (정확히는 헤더가 가리키고 있는) 것이다.
이런 튜링머신은 Transducer로서 동작하는 튜링머신과 같다.

트랜스듀서로서 TM을 활용하는 예시는 위와 같은 예시가 있다.
양수에 대한 덧셈을 수행하거나 1로 구성된 문자열을 복사하거나, 간단한 결정을 할 수 있따.
9.9 양수에 대한 덧셈은 input 에 1을 그 만큼 넣어두고 합친다고 생각해보면 좋다.
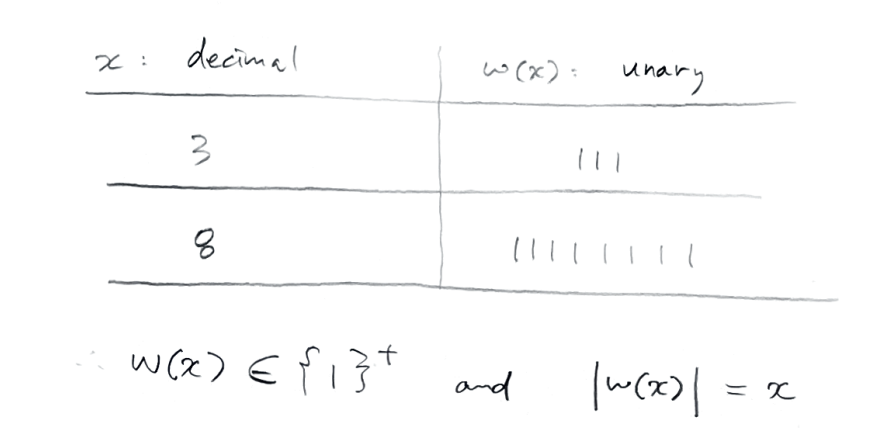
즉, 이렇게 표현할 수 있다.

그러면, 3+2 를 한다는 것은 111 0 11 으로 테이프에 넣어두고 (0은 구분자)
뭔가 열심히 computation을 돌려서 halt 된 결과 를 instantaneous description 으로 나타내면 qf 111110 과 같이 되어있기만 하면 된다. (이때 0은 여기가 끝이다! 라는 것을 알려주는 용도로 활용될 것이다.)
그리고 이를 튜링머신으로 계산한다는 것은, 1을 만나면 유지하면서 오른쪽으로 가다가, 0을 만났으면 구분자를 만났으니 두번째 수를 읽는 상태로 바꿔주면서 1을 왼쪽으로 1칸씩 옮겨주면 된다.
최종적으로 블랭크를 만나면 다 읽었으니 그 위치에 0을 써주고 마치면 된다.

move 로는 위와 같이 표현할 수 있었고, 기계의 트랜지션 함수는 이렇게 정의하면 된다.
q0 는 왼쪽 피연산자를 읽는 상태, q1은 오른쪽 피연산자를 읽는 상태
q2는 오른쪽 피연산자를 다 읽은 상태이지만 아직 마지막 1을 바꾸지 않은 상태
q3 는 마지막 1을 0으로 바꿔주고, 헤드를 연산 시작점으로 돌아가는 상태이다.
트랜스듀서로서 동작하려면 테이프에 연산 결과를 저장히기 위해 헤더의 위치도 조정해주기 위해 위와 같이 표현해야 한다.

예시를 넣었을 때 move 의 진행 과정과, 트랜지션 그래프를 그렸을 때의 모습은 위와 같다.

1을 복사하는 예시도 살펴보면

i.d 로 표현했을 때는 q0에서 w를 넣었다면 연산이 종료되었을 때, qf 가 있고 그 옆에 ww가 있으면 된다.
이를 튜링 머신으로 구현하는 기본적인 아이디어는 모든 1을 x로 바꾸고,
x를 읽을 때마다 2개의 1을 추가해주면 된다.

1을 만나면 x로 바꾸면서 오른쪽으로 가다가 blank를 만나면 왼쪽으로 포인터를 옮긴다.
111 이었다면 xxx 가 되고 제일 오른쪽의 x를 가리키고 있을 것이다.
이제 왼쪽으로 이동하면서 1을 추가해줄텐데, x를 읽게 되면 해당 x를 1로 바꾸고 오른쪽으로 이동한다.
xxx 에서 xx1 이 되는 것이다. 그리고 블랭크를 가리키고 있을 텐데,
q2 상태에서 블랭크를 읽으면 1을 추가하고 왼쪽으로 이동한다.
새롭게 복사된 1이 입력되었으므로 이제 x를 만날 때까지 헤더를 왼쪽으로 옮겨준다.
xx11 이 된 상태에서 x를 만나면 다시 x를 1로 바꿔주고, 맨 끝에 블랭크를 만날 때까지 이동해서 블랭크에 1을 써준다.
x1111 이 된 상태에서 다시 왼쪽으로 이동해 x를 만나면 1로 바꿔주고 맨 끝 블랭크에 1을 써준 뒤 다시 왼쪽으로 이동한다.
111111 이 된 상태에서 x 가 아니라 블랭크를 만나면 다 처리햇다는 뜻이니 final state로 이동하고 포인터를 오른쪽으로 옮겨서 1을 가리키게 해주면 된다.
마지막 예시 (simple decision)는 아이디어만 정리한다. (시험에는 안 내신다고 하심)

마지막 문제는 두 개의 값이 주어질 때, 그 크기를 비교해서 final / non-fianl 로 끝내는 것을 말한다.
기본적인 아이디어는 두 값을 모두 1을 그 크기만큼 나열한 뒤 구분자 (0) 으로 한 칸 띄워주고
각각 제일 왼쪽에 있는 1을 모두 x로 균등하게 바꿔주면서 착착 나가다가 오른쪽 피연산자에서 더 이상 x로 바꿀 1이 없다면 왼쪽 피연산자가 더 큰 것이다.

그래서 이렇게 3가지 케이스를 나누어서 처리해주면 된다.
'CS > 오토마타' 카테고리의 다른 글
| [오토마타] 24. RL vs CFL vs TM (0) | 2024.12.12 |
|---|---|
| [오토마타] 22. CFL의 Closure Property (0) | 2024.12.12 |
| [오토마타] 21. Pummping Lemma (for CFL) (0) | 2024.12.12 |
| [오토마타] 20. DPDA & DCFL (0) | 2024.12.12 |
| [오토마타] 19. NPDA & CFL (0) | 2024.12.12 |
